problem
stringlengths 5
10.4k
| solution
stringlengths 1
24.1k
| answer
stringlengths 1
250
⌀ | problem_is_valid
stringclasses 4
values | solution_is_valid
stringclasses 4
values | question_type
stringclasses 4
values | problem_type
stringclasses 8
values | problem_raw
stringlengths 5
10.4k
| solution_raw
stringlengths 1
24.1k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 10k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
Let $x_{1}, x_{2}, \ldots, x_{n}$ be positive real numbers, and let
$$
S=x_{1}+x_{2}+\cdots+x_{n}
$$
Prove that
$$
\left(1+x_{1}\right)\left(1+x_{2}\right) \cdots\left(1+x_{n}\right) \leq 1+S+\frac{S^{2}}{2!}+\frac{S^{3}}{3!}+\cdots+\frac{S^{n}}{n!}
$$
|
Let $\sigma_{k}$ be the $k$ th symmetric polynomial, namely
$$
\sigma_{k}=\sum_{\substack{|S|=k \\ S \subseteq\{1,2, \ldots, n\}}} \prod_{i \in S} x_{i},
$$
and more explicitly
$$
\sigma_{1}=S, \quad \sigma_{2}=x_{1} x_{2}+x_{1} x_{3}+\cdots+x_{n-1} x_{n}, \quad \text { and so on. }
$$
Then
$$
\left(1+x_{1}\right)\left(1+x_{2}\right) \cdots\left(1+x_{n}\right)=1+\sigma_{1}+\sigma_{2}+\cdots+\sigma_{n}
$$
The expansion of
$$
S^{k}=\left(x_{1}+x_{2}+\cdots+x_{n}\right)^{k}=\underbrace{\left(x_{1}+x_{2}+\cdots+x_{n}\right)\left(x_{1}+x_{2}+\cdots+x_{n}\right) \cdots\left(x_{1}+x_{2}+\cdots+x_{n}\right)}_{k \text { times }}
$$
has at least $k$ ! occurrences of $\prod_{i \in S} x_{i}$ for each subset $S$ with $k$ indices from $\{1,2, \ldots, n\}$. In fact, if $\pi$ is a permutation of $S$, we can choose each $x_{\pi(i)}$ from the $i$ th factor of $\left(x_{1}+x_{2}+\cdots+x_{n}\right)^{k}$. Then each term appears at least $k$ ! times, and
$$
S^{k} \geq k!\sigma_{k} \Longleftrightarrow \sigma_{k} \leq \frac{S^{k}}{k!}
$$
Summing the obtained inequalities for $k=1,2, \ldots, n$ yields the result.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $x_{1}, x_{2}, \ldots, x_{n}$ be positive real numbers, and let
$$
S=x_{1}+x_{2}+\cdots+x_{n}
$$
Prove that
$$
\left(1+x_{1}\right)\left(1+x_{2}\right) \cdots\left(1+x_{n}\right) \leq 1+S+\frac{S^{2}}{2!}+\frac{S^{3}}{3!}+\cdots+\frac{S^{n}}{n!}
$$
|
Let $\sigma_{k}$ be the $k$ th symmetric polynomial, namely
$$
\sigma_{k}=\sum_{\substack{|S|=k \\ S \subseteq\{1,2, \ldots, n\}}} \prod_{i \in S} x_{i},
$$
and more explicitly
$$
\sigma_{1}=S, \quad \sigma_{2}=x_{1} x_{2}+x_{1} x_{3}+\cdots+x_{n-1} x_{n}, \quad \text { and so on. }
$$
Then
$$
\left(1+x_{1}\right)\left(1+x_{2}\right) \cdots\left(1+x_{n}\right)=1+\sigma_{1}+\sigma_{2}+\cdots+\sigma_{n}
$$
The expansion of
$$
S^{k}=\left(x_{1}+x_{2}+\cdots+x_{n}\right)^{k}=\underbrace{\left(x_{1}+x_{2}+\cdots+x_{n}\right)\left(x_{1}+x_{2}+\cdots+x_{n}\right) \cdots\left(x_{1}+x_{2}+\cdots+x_{n}\right)}_{k \text { times }}
$$
has at least $k$ ! occurrences of $\prod_{i \in S} x_{i}$ for each subset $S$ with $k$ indices from $\{1,2, \ldots, n\}$. In fact, if $\pi$ is a permutation of $S$, we can choose each $x_{\pi(i)}$ from the $i$ th factor of $\left(x_{1}+x_{2}+\cdots+x_{n}\right)^{k}$. Then each term appears at least $k$ ! times, and
$$
S^{k} \geq k!\sigma_{k} \Longleftrightarrow \sigma_{k} \leq \frac{S^{k}}{k!}
$$
Summing the obtained inequalities for $k=1,2, \ldots, n$ yields the result.
|
{
"resource_path": "APMO/segmented/en-apmo1989_sol.jsonl",
"problem_match": "# Problem 1",
"solution_match": "# Solution 1"
}
|
b68eb2f6-098f-5fca-a42e-60c8dd41aef2
| 604,152
|
Let $x_{1}, x_{2}, \ldots, x_{n}$ be positive real numbers, and let
$$
S=x_{1}+x_{2}+\cdots+x_{n}
$$
Prove that
$$
\left(1+x_{1}\right)\left(1+x_{2}\right) \cdots\left(1+x_{n}\right) \leq 1+S+\frac{S^{2}}{2!}+\frac{S^{3}}{3!}+\cdots+\frac{S^{n}}{n!}
$$
|
By AM-GM,
$$
\left(1+x_{1}\right)\left(1+x_{2}\right) \cdots\left(1+x_{n}\right) \leq\left(\frac{\left(1+x_{1}\right)+\left(1+x_{2}\right)+\cdots+\left(1+x_{n}\right)}{n}\right)^{n}=\left(1+\frac{S}{n}\right)^{n}
$$
By the binomial theorem,
$$
\left(1+\frac{S}{n}\right)^{n}=\sum_{k=0}^{n}\binom{n}{k}\left(\frac{S}{n}\right)^{k}=\sum_{k=0}^{n} \frac{1}{k!} \frac{n(n-1) \ldots(n-k+1)}{n^{k}} S^{k} \leq \sum_{k=0}^{n} \frac{S^{k}}{k!}
$$
and the result follows.
Comment: Maclaurin's inequality states that
$$
\frac{\sigma_{1}}{n} \geq \sqrt{\frac{\sigma_{2}}{\binom{n}{2}}} \geq \cdots \geq \sqrt[k]{\frac{\sigma_{k}}{\binom{n}{k}}} \geq \cdots \geq \sqrt[n]{\frac{\sigma_{n}}{\binom{n}{n}}}
$$
Then $\sigma_{k} \leq\binom{ n}{k} \frac{S^{k}}{n^{k}}=\frac{1}{k!} \frac{n(n-1) \ldots(n-k+1)}{n^{k}} S^{k} \leq \frac{S^{k}}{k!}$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $x_{1}, x_{2}, \ldots, x_{n}$ be positive real numbers, and let
$$
S=x_{1}+x_{2}+\cdots+x_{n}
$$
Prove that
$$
\left(1+x_{1}\right)\left(1+x_{2}\right) \cdots\left(1+x_{n}\right) \leq 1+S+\frac{S^{2}}{2!}+\frac{S^{3}}{3!}+\cdots+\frac{S^{n}}{n!}
$$
|
By AM-GM,
$$
\left(1+x_{1}\right)\left(1+x_{2}\right) \cdots\left(1+x_{n}\right) \leq\left(\frac{\left(1+x_{1}\right)+\left(1+x_{2}\right)+\cdots+\left(1+x_{n}\right)}{n}\right)^{n}=\left(1+\frac{S}{n}\right)^{n}
$$
By the binomial theorem,
$$
\left(1+\frac{S}{n}\right)^{n}=\sum_{k=0}^{n}\binom{n}{k}\left(\frac{S}{n}\right)^{k}=\sum_{k=0}^{n} \frac{1}{k!} \frac{n(n-1) \ldots(n-k+1)}{n^{k}} S^{k} \leq \sum_{k=0}^{n} \frac{S^{k}}{k!}
$$
and the result follows.
Comment: Maclaurin's inequality states that
$$
\frac{\sigma_{1}}{n} \geq \sqrt{\frac{\sigma_{2}}{\binom{n}{2}}} \geq \cdots \geq \sqrt[k]{\frac{\sigma_{k}}{\binom{n}{k}}} \geq \cdots \geq \sqrt[n]{\frac{\sigma_{n}}{\binom{n}{n}}}
$$
Then $\sigma_{k} \leq\binom{ n}{k} \frac{S^{k}}{n^{k}}=\frac{1}{k!} \frac{n(n-1) \ldots(n-k+1)}{n^{k}} S^{k} \leq \frac{S^{k}}{k!}$.
|
{
"resource_path": "APMO/segmented/en-apmo1989_sol.jsonl",
"problem_match": "# Problem 1",
"solution_match": "# Solution 2"
}
|
b68eb2f6-098f-5fca-a42e-60c8dd41aef2
| 604,152
|
Prove that the equation
$$
6\left(6 a^{2}+3 b^{2}+c^{2}\right)=5 n^{2}
$$
has no solutions in integers except $a=b=c=n=0$.
|
We can suppose without loss of generality that $a, b, c, n \geq 0$. Let $(a, b, c, n)$ be a solution with minimum sum $a+b+c+n$. Suppose, for the sake of contradiction, that $a+b+c+n>0$. Since 6 divides $5 n^{2}, n$ is a multiple of 6 . Let $n=6 n_{0}$. Then the equation reduces to
$$
6 a^{2}+3 b^{2}+c^{2}=30 n_{0}^{2}
$$
The number $c$ is a multiple of 3 , so let $c=3 c_{0}$. The equation now reduces to
$$
2 a^{2}+b^{2}+3 c_{0}^{2}=10 n_{0}^{2}
$$
Now look at the equation modulo 8:
$$
b^{2}+3 c_{0}^{2} \equiv 2\left(n_{0}^{2}-a^{2}\right) \quad(\bmod 8)
$$
Integers $b$ and $c_{0}$ have the same parity. Either way, since $x^{2}$ is congruent to 0 or 1 modulo 4 , $b^{2}+3 c_{0}^{2}$ is a multiple of 4 , so $n_{0}^{2}-a^{2}=\left(n_{0}-a\right)\left(n_{0}+a\right)$ is even, and therefore also a multiple of 4 , since $n_{0}-a$ and $n_{0}+a$ have the same parity. Hence $2\left(n_{0}^{2}-a^{2}\right)$ is a multiple of 8 , and
$$
b^{2}+3 c_{0}^{2} \equiv 0 \quad(\bmod 8)
$$
If $b$ and $c_{0}$ are both odd, $b^{2}+3 c_{0}^{2} \equiv 4(\bmod 8)$, which is impossible. Then $b$ and $c_{0}$ are both even. Let $b=2 b_{0}$ and $c_{0}=2 c_{1}$, and we find
$$
a^{2}+2 b_{0}^{2}+6 c_{1}^{2}=5 n_{0}^{2}
$$
Look at the last equation modulo 8:
$$
a^{2}+3 n_{0}^{2} \equiv 2\left(c_{1}^{2}-b_{0}^{2}\right) \quad(\bmod 8)
$$
A similar argument shows that $a$ and $n_{0}$ are both even.
We have proven that $a, b, c, n$ are all even. Then, dividing the original equation by 4 we find
$$
6\left(6(a / 2)^{2}+3(b / 2)^{2}+(c / 2)^{2}\right)=5(n / 2)^{2}
$$
and we find that $(a / 2, b / 2, c / 2, n / 2)$ is a new solution with smaller sum. This is a contradiction, and the only solution is $(a, b, c, n)=(0,0,0,0)$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that the equation
$$
6\left(6 a^{2}+3 b^{2}+c^{2}\right)=5 n^{2}
$$
has no solutions in integers except $a=b=c=n=0$.
|
We can suppose without loss of generality that $a, b, c, n \geq 0$. Let $(a, b, c, n)$ be a solution with minimum sum $a+b+c+n$. Suppose, for the sake of contradiction, that $a+b+c+n>0$. Since 6 divides $5 n^{2}, n$ is a multiple of 6 . Let $n=6 n_{0}$. Then the equation reduces to
$$
6 a^{2}+3 b^{2}+c^{2}=30 n_{0}^{2}
$$
The number $c$ is a multiple of 3 , so let $c=3 c_{0}$. The equation now reduces to
$$
2 a^{2}+b^{2}+3 c_{0}^{2}=10 n_{0}^{2}
$$
Now look at the equation modulo 8:
$$
b^{2}+3 c_{0}^{2} \equiv 2\left(n_{0}^{2}-a^{2}\right) \quad(\bmod 8)
$$
Integers $b$ and $c_{0}$ have the same parity. Either way, since $x^{2}$ is congruent to 0 or 1 modulo 4 , $b^{2}+3 c_{0}^{2}$ is a multiple of 4 , so $n_{0}^{2}-a^{2}=\left(n_{0}-a\right)\left(n_{0}+a\right)$ is even, and therefore also a multiple of 4 , since $n_{0}-a$ and $n_{0}+a$ have the same parity. Hence $2\left(n_{0}^{2}-a^{2}\right)$ is a multiple of 8 , and
$$
b^{2}+3 c_{0}^{2} \equiv 0 \quad(\bmod 8)
$$
If $b$ and $c_{0}$ are both odd, $b^{2}+3 c_{0}^{2} \equiv 4(\bmod 8)$, which is impossible. Then $b$ and $c_{0}$ are both even. Let $b=2 b_{0}$ and $c_{0}=2 c_{1}$, and we find
$$
a^{2}+2 b_{0}^{2}+6 c_{1}^{2}=5 n_{0}^{2}
$$
Look at the last equation modulo 8:
$$
a^{2}+3 n_{0}^{2} \equiv 2\left(c_{1}^{2}-b_{0}^{2}\right) \quad(\bmod 8)
$$
A similar argument shows that $a$ and $n_{0}$ are both even.
We have proven that $a, b, c, n$ are all even. Then, dividing the original equation by 4 we find
$$
6\left(6(a / 2)^{2}+3(b / 2)^{2}+(c / 2)^{2}\right)=5(n / 2)^{2}
$$
and we find that $(a / 2, b / 2, c / 2, n / 2)$ is a new solution with smaller sum. This is a contradiction, and the only solution is $(a, b, c, n)=(0,0,0,0)$.
|
{
"resource_path": "APMO/segmented/en-apmo1989_sol.jsonl",
"problem_match": "# Problem 2",
"solution_match": "# Solution\n\n"
}
|
f926320b-a7a4-5a7e-adab-23b4749bfd74
| 604,164
|
Let $A_{1}, A_{2}, A_{3}$ be three points in the plane, and for convenience,let $A_{4}=A_{1}, A_{5}=A_{2}$. For $n=1,2$, and 3 , suppose that $B_{n}$ is the midpoint of $A_{n} A_{n+1}$, and suppose that $C_{n}$ is the midpoint of $A_{n} B_{n}$. Suppose that $A_{n} C_{n+1}$ and $B_{n} A_{n+2}$ meet at $D_{n}$, and that $A_{n} B_{n+1}$ and $C_{n} A_{n+2}$ meet at $E_{n}$. Calculate the ratio of the area of triangle $D_{1} D_{2} D_{3}$ to the area of triangle $E_{1} E_{2} E_{3}$.
Answer: $\frac{25}{49}$.
|
Let $G$ be the centroid of triangle $A B C$, and also the intersection point of $A_{1} B_{2}, A_{2} B_{3}$, and $A_{3} B_{1}$ 。
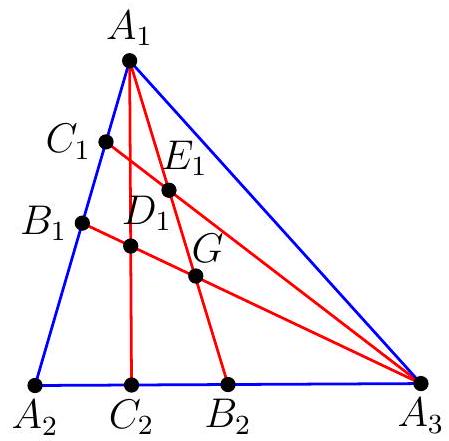
By Menelao's theorem on triangle $B_{1} A_{2} A_{3}$ and line $A_{1} D_{1} C_{2}$,
$$
\frac{A_{1} B_{1}}{A_{1} A_{2}} \cdot \frac{D_{1} A_{3}}{D_{1} B_{1}} \cdot \frac{C_{2} A_{2}}{C_{2} A_{3}}=1 \Longleftrightarrow \frac{D_{1} A_{3}}{D_{1} B_{1}}=2 \cdot 3=6 \Longleftrightarrow \frac{D_{1} B_{1}}{A_{3} B_{1}}=\frac{1}{7}
$$
Since $A_{3} G=\frac{2}{3} A_{3} B_{1}$, if $A_{3} B_{1}=21 t$ then $G A_{3}=14 t, D_{1} B_{1}=\frac{21 t}{7}=3 t, A_{3} D_{1}=18 t$, and $G D_{1}=A_{3} D_{1}-A_{3} G=18 t-14 t=4 t$, and
$$
\frac{G D_{1}}{G A_{3}}=\frac{4}{14}=\frac{2}{7}
$$
Similar results hold for the other medians, therefore $D_{1} D_{2} D_{3}$ and $A_{1} A_{2} A_{3}$ are homothetic with center $G$ and ratio $-\frac{2}{7}$.
By Menelao's theorem on triangle $A_{1} A_{2} B_{2}$ and line $C_{1} E_{1} A_{3}$,
$$
\frac{C_{1} A_{1}}{C_{1} A_{2}} \cdot \frac{E_{1} B_{2}}{E_{1} A_{1}} \cdot \frac{A_{3} A_{2}}{A_{3} B_{2}}=1 \Longleftrightarrow \frac{E_{1} B_{2}}{E_{1} A_{1}}=3 \cdot \frac{1}{2}=\frac{3}{2} \Longleftrightarrow \frac{A_{1} E_{1}}{A_{1} B_{2}}=\frac{2}{5}
$$
If $A_{1} B_{2}=15 u$, then $A_{1} G=\frac{2}{3} \cdot 15 u=10 u$ and $G E_{1}=A_{1} G-A_{1} E_{1}=10 u-\frac{2}{5} \cdot 15 u=4 u$, and
$$
\frac{G E_{1}}{G A_{1}}=\frac{4}{10}=\frac{2}{5}
$$
Similar results hold for the other medians, therefore $E_{1} E_{2} E_{3}$ and $A_{1} A_{2} A_{3}$ are homothetic with center $G$ and ratio $\frac{2}{5}$.
Then $D_{1} D_{2} D_{3}$ and $E_{1} E_{2} E_{3}$ are homothetic with center $G$ and ratio $-\frac{2}{7}: \frac{2}{5}=-\frac{5}{7}$, and the ratio of their area is $\left(\frac{5}{7}\right)^{2}=\frac{25}{49}$.
|
\frac{25}{49}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A_{1}, A_{2}, A_{3}$ be three points in the plane, and for convenience,let $A_{4}=A_{1}, A_{5}=A_{2}$. For $n=1,2$, and 3 , suppose that $B_{n}$ is the midpoint of $A_{n} A_{n+1}$, and suppose that $C_{n}$ is the midpoint of $A_{n} B_{n}$. Suppose that $A_{n} C_{n+1}$ and $B_{n} A_{n+2}$ meet at $D_{n}$, and that $A_{n} B_{n+1}$ and $C_{n} A_{n+2}$ meet at $E_{n}$. Calculate the ratio of the area of triangle $D_{1} D_{2} D_{3}$ to the area of triangle $E_{1} E_{2} E_{3}$.
Answer: $\frac{25}{49}$.
|
Let $G$ be the centroid of triangle $A B C$, and also the intersection point of $A_{1} B_{2}, A_{2} B_{3}$, and $A_{3} B_{1}$ 。

By Menelao's theorem on triangle $B_{1} A_{2} A_{3}$ and line $A_{1} D_{1} C_{2}$,
$$
\frac{A_{1} B_{1}}{A_{1} A_{2}} \cdot \frac{D_{1} A_{3}}{D_{1} B_{1}} \cdot \frac{C_{2} A_{2}}{C_{2} A_{3}}=1 \Longleftrightarrow \frac{D_{1} A_{3}}{D_{1} B_{1}}=2 \cdot 3=6 \Longleftrightarrow \frac{D_{1} B_{1}}{A_{3} B_{1}}=\frac{1}{7}
$$
Since $A_{3} G=\frac{2}{3} A_{3} B_{1}$, if $A_{3} B_{1}=21 t$ then $G A_{3}=14 t, D_{1} B_{1}=\frac{21 t}{7}=3 t, A_{3} D_{1}=18 t$, and $G D_{1}=A_{3} D_{1}-A_{3} G=18 t-14 t=4 t$, and
$$
\frac{G D_{1}}{G A_{3}}=\frac{4}{14}=\frac{2}{7}
$$
Similar results hold for the other medians, therefore $D_{1} D_{2} D_{3}$ and $A_{1} A_{2} A_{3}$ are homothetic with center $G$ and ratio $-\frac{2}{7}$.
By Menelao's theorem on triangle $A_{1} A_{2} B_{2}$ and line $C_{1} E_{1} A_{3}$,
$$
\frac{C_{1} A_{1}}{C_{1} A_{2}} \cdot \frac{E_{1} B_{2}}{E_{1} A_{1}} \cdot \frac{A_{3} A_{2}}{A_{3} B_{2}}=1 \Longleftrightarrow \frac{E_{1} B_{2}}{E_{1} A_{1}}=3 \cdot \frac{1}{2}=\frac{3}{2} \Longleftrightarrow \frac{A_{1} E_{1}}{A_{1} B_{2}}=\frac{2}{5}
$$
If $A_{1} B_{2}=15 u$, then $A_{1} G=\frac{2}{3} \cdot 15 u=10 u$ and $G E_{1}=A_{1} G-A_{1} E_{1}=10 u-\frac{2}{5} \cdot 15 u=4 u$, and
$$
\frac{G E_{1}}{G A_{1}}=\frac{4}{10}=\frac{2}{5}
$$
Similar results hold for the other medians, therefore $E_{1} E_{2} E_{3}$ and $A_{1} A_{2} A_{3}$ are homothetic with center $G$ and ratio $\frac{2}{5}$.
Then $D_{1} D_{2} D_{3}$ and $E_{1} E_{2} E_{3}$ are homothetic with center $G$ and ratio $-\frac{2}{7}: \frac{2}{5}=-\frac{5}{7}$, and the ratio of their area is $\left(\frac{5}{7}\right)^{2}=\frac{25}{49}$.
|
{
"resource_path": "APMO/segmented/en-apmo1989_sol.jsonl",
"problem_match": "# Problem 3",
"solution_match": "\nSolution\n"
}
|
83c5357e-cc64-51e7-8925-9bd682bff7b7
| 604,178
|
Let $S$ be a set consisting of $m$ pairs $(a, b)$ of positive integers with the property that $1 \leq a<$ $b \leq n$. Show that there are at least
$$
4 m \frac{\left(m-\frac{n^{2}}{4}\right)}{3 n}
$$
triples $(a, b, c)$ such that $(a, b),(a, c)$, and $(b, c)$ belong to $S$.
|
Call a triple $(a, b, c)$ good if and only if $(a, b),(a, c)$, and $(b, c)$ all belong to $S$. For $i$ in $\{1,2, \ldots, n\}$, let $d_{i}$ be the number of pairs in $S$ that contain $i$, and let $D_{i}$ be the set of numbers paired with $i$ in $S$ (so $\left|D_{i}\right|=d_{i}$ ). Consider a pair $(i, j) \in S$. Our goal is to estimate the number of integers $k$ such that any permutation of $\{i, j, k\}$ is good, that is, $\left|D_{i} \cap D_{j}\right|$. Note that $i \notin D_{i}$ and $j \notin D_{j}$, so $i, j \notin D_{i} \cap D_{j}$; thus any $k \in D_{i} \cap D_{j}$ is different from both $i$ and $j$, and $\{i, j, k\}$ has three elements as required. Now, since $D_{i} \cup D_{j} \subseteq\{1,2, \ldots, n\}$,
$$
\left|D_{i} \cap D_{j}\right|=\left|D_{i}\right|+\left|D_{j}\right|-\left|D_{i} \cup D_{j}\right| \leq d_{i}+d_{j}-n
$$
Summing all the results, and having in mind that each good triple is counted three times (one for each two of the three numbers), the number of good triples $T$ is at least
$$
T \geq \frac{1}{3} \sum_{(i, j) \in S}\left(d_{i}+d_{j}-n\right)
$$
Each term $d_{i}$ appears each time $i$ is in a pair from $S$, that is, $d_{i}$ times; there are $m$ pairs in $S$, so $n$ is subtracted $m$ times. By the Cauchy-Schwartz inequality
$$
T \geq \frac{1}{3}\left(\sum_{i=1}^{n} d_{i}^{2}-m n\right) \geq \frac{1}{3}\left(\frac{\left(\sum_{i=1}^{n} d_{i}\right)^{2}}{n}-m n\right) .
$$
Finally, the sum $\sum_{i=1}^{n} d_{i}$ is $2 m$, since $d_{i}$ counts the number of pairs containing $i$, and each pair $(i, j)$ is counted twice: once in $d_{i}$ and once in $d_{j}$. Therefore
$$
T \geq \frac{1}{3}\left(\frac{(2 m)^{2}}{n}-m n\right)=4 m \frac{\left(m-\frac{n^{2}}{4}\right)}{3 n} .
$$
Comment: This is a celebrated graph theory fact named Goodman's bound, after A. M. Goodman's method published in 1959. The generalized version of the problem is still studied to this day.
|
4 m \frac{\left(m-\frac{n^{2}}{4}\right)}{3 n}
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $S$ be a set consisting of $m$ pairs $(a, b)$ of positive integers with the property that $1 \leq a<$ $b \leq n$. Show that there are at least
$$
4 m \frac{\left(m-\frac{n^{2}}{4}\right)}{3 n}
$$
triples $(a, b, c)$ such that $(a, b),(a, c)$, and $(b, c)$ belong to $S$.
|
Call a triple $(a, b, c)$ good if and only if $(a, b),(a, c)$, and $(b, c)$ all belong to $S$. For $i$ in $\{1,2, \ldots, n\}$, let $d_{i}$ be the number of pairs in $S$ that contain $i$, and let $D_{i}$ be the set of numbers paired with $i$ in $S$ (so $\left|D_{i}\right|=d_{i}$ ). Consider a pair $(i, j) \in S$. Our goal is to estimate the number of integers $k$ such that any permutation of $\{i, j, k\}$ is good, that is, $\left|D_{i} \cap D_{j}\right|$. Note that $i \notin D_{i}$ and $j \notin D_{j}$, so $i, j \notin D_{i} \cap D_{j}$; thus any $k \in D_{i} \cap D_{j}$ is different from both $i$ and $j$, and $\{i, j, k\}$ has three elements as required. Now, since $D_{i} \cup D_{j} \subseteq\{1,2, \ldots, n\}$,
$$
\left|D_{i} \cap D_{j}\right|=\left|D_{i}\right|+\left|D_{j}\right|-\left|D_{i} \cup D_{j}\right| \leq d_{i}+d_{j}-n
$$
Summing all the results, and having in mind that each good triple is counted three times (one for each two of the three numbers), the number of good triples $T$ is at least
$$
T \geq \frac{1}{3} \sum_{(i, j) \in S}\left(d_{i}+d_{j}-n\right)
$$
Each term $d_{i}$ appears each time $i$ is in a pair from $S$, that is, $d_{i}$ times; there are $m$ pairs in $S$, so $n$ is subtracted $m$ times. By the Cauchy-Schwartz inequality
$$
T \geq \frac{1}{3}\left(\sum_{i=1}^{n} d_{i}^{2}-m n\right) \geq \frac{1}{3}\left(\frac{\left(\sum_{i=1}^{n} d_{i}\right)^{2}}{n}-m n\right) .
$$
Finally, the sum $\sum_{i=1}^{n} d_{i}$ is $2 m$, since $d_{i}$ counts the number of pairs containing $i$, and each pair $(i, j)$ is counted twice: once in $d_{i}$ and once in $d_{j}$. Therefore
$$
T \geq \frac{1}{3}\left(\frac{(2 m)^{2}}{n}-m n\right)=4 m \frac{\left(m-\frac{n^{2}}{4}\right)}{3 n} .
$$
Comment: This is a celebrated graph theory fact named Goodman's bound, after A. M. Goodman's method published in 1959. The generalized version of the problem is still studied to this day.
|
{
"resource_path": "APMO/segmented/en-apmo1989_sol.jsonl",
"problem_match": "# Problem 4",
"solution_match": "# Solution\n\n"
}
|
d69db721-1dc2-54fb-a7ff-782194933133
| 604,193
|
Determine all functions $f$ from the reals to the reals for which
(1) $f(x)$ is strictly increasing,
(2) $f(x)+g(x)=2 x$ for all real $x$, where $g(x)$ is the composition inverse function to $f(x)$.
(Note: $f$ and $g$ are said to be composition inverses if $f(g(x))=x$ and $g(f(x))=x$ for all real x.)
Answer: $f(x)=x+c, c \in \mathbb{R}$ constant.
|
Denote by $f_{n}$ the $n$th iterate of $f$, that is, $f_{n}(x)=\underbrace{f(f(\ldots f}_{n \text { times }}(x)))$.
Plug $x \rightarrow f_{n+1}(x)$ in (2): since $g\left(f_{n+1}(x)\right)=g\left(f\left(f_{n}(x)\right)\right)=f_{n}(x)$,
$$
f_{n+2}(x)+f_{n}(x)=2 f_{n+1}(x)
$$
that is,
$$
f_{n+2}(x)-f_{n+1}(x)=f_{n+1}(x)-f_{n}(x)
$$
Therefore $f_{n}(x)-f_{n-1}(x)$ does not depend on $n$, and is equal to $f(x)-x$. Summing the corresponding results for smaller values of $n$ we find
$$
f_{n}(x)-x=n(f(x)-x) .
$$
Since $g$ has the same properties as $f$,
$$
g_{n}(x)-x=n(g(x)-x)=-n(f(x)-x) .
$$
Finally, $g$ is also increasing, because since $f$ is increasing $g(x)>g(y) \Longrightarrow f(g(x))>$ $f(g(y)) \Longrightarrow x>y$. An induction proves that $f_{n}$ and $g_{n}$ are also increasing functions.
Let $x>y$ be real numbers. Since $f_{n}$ and $g_{n}$ are increasing,
$$
x+n(f(x)-x)>y+n(f(y)-y) \Longleftrightarrow n[(f(x)-x)-(f(y)-y)]>y-x
$$
and
$$
x-n(f(x)-x)>y-n(f(y)-y) \Longleftrightarrow n[(f(x)-x)-(f(y)-y)]<x-y
$$
Summing it up,
$$
|n[(f(x)-x)-(f(y)-y)]|<x-y \quad \text { for all } n \in \mathbb{Z}_{>0}
$$
Suppose that $a=f(x)-x$ and $b=f(y)-y$ are distinct. Then, for all positive integers $n$,
$$
|n(a-b)|<x-y
$$
which is false for a sufficiently large $n$. Hence $a=b$, and $f(x)-x$ is a constant $c$ for all $x \in \mathbb{R}$, that is, $f(x)=x+c$.
It is immediate that $f(x)=x+c$ satisfies the problem, as $g(x)=x-c$.
|
f(x)=x+c
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Determine all functions $f$ from the reals to the reals for which
(1) $f(x)$ is strictly increasing,
(2) $f(x)+g(x)=2 x$ for all real $x$, where $g(x)$ is the composition inverse function to $f(x)$.
(Note: $f$ and $g$ are said to be composition inverses if $f(g(x))=x$ and $g(f(x))=x$ for all real x.)
Answer: $f(x)=x+c, c \in \mathbb{R}$ constant.
|
Denote by $f_{n}$ the $n$th iterate of $f$, that is, $f_{n}(x)=\underbrace{f(f(\ldots f}_{n \text { times }}(x)))$.
Plug $x \rightarrow f_{n+1}(x)$ in (2): since $g\left(f_{n+1}(x)\right)=g\left(f\left(f_{n}(x)\right)\right)=f_{n}(x)$,
$$
f_{n+2}(x)+f_{n}(x)=2 f_{n+1}(x)
$$
that is,
$$
f_{n+2}(x)-f_{n+1}(x)=f_{n+1}(x)-f_{n}(x)
$$
Therefore $f_{n}(x)-f_{n-1}(x)$ does not depend on $n$, and is equal to $f(x)-x$. Summing the corresponding results for smaller values of $n$ we find
$$
f_{n}(x)-x=n(f(x)-x) .
$$
Since $g$ has the same properties as $f$,
$$
g_{n}(x)-x=n(g(x)-x)=-n(f(x)-x) .
$$
Finally, $g$ is also increasing, because since $f$ is increasing $g(x)>g(y) \Longrightarrow f(g(x))>$ $f(g(y)) \Longrightarrow x>y$. An induction proves that $f_{n}$ and $g_{n}$ are also increasing functions.
Let $x>y$ be real numbers. Since $f_{n}$ and $g_{n}$ are increasing,
$$
x+n(f(x)-x)>y+n(f(y)-y) \Longleftrightarrow n[(f(x)-x)-(f(y)-y)]>y-x
$$
and
$$
x-n(f(x)-x)>y-n(f(y)-y) \Longleftrightarrow n[(f(x)-x)-(f(y)-y)]<x-y
$$
Summing it up,
$$
|n[(f(x)-x)-(f(y)-y)]|<x-y \quad \text { for all } n \in \mathbb{Z}_{>0}
$$
Suppose that $a=f(x)-x$ and $b=f(y)-y$ are distinct. Then, for all positive integers $n$,
$$
|n(a-b)|<x-y
$$
which is false for a sufficiently large $n$. Hence $a=b$, and $f(x)-x$ is a constant $c$ for all $x \in \mathbb{R}$, that is, $f(x)=x+c$.
It is immediate that $f(x)=x+c$ satisfies the problem, as $g(x)=x-c$.
|
{
"resource_path": "APMO/segmented/en-apmo1989_sol.jsonl",
"problem_match": "# Problem 5",
"solution_match": "# Solution\n\n"
}
|
ff46dcd7-7e93-54e5-807f-4bc409a74a07
| 604,207
|
In $\triangle A B C$, let $D, E, F$ be the midpoints of $B C, A C, A B$ respectively and let $G$ be the centroid of the triangle.
For each value of $\angle B A C$, how many non-similar triangles are there in which $A E G F$ is a cyclic quadrilateral?
|
Let $I$ be the intersection of $A G$ and $E F$.
Let $\delta=A I . I G-F I$ IE. Then
$$
A I=A D / 2, \quad I G=A D / 6, \quad F I=B C / 4=I E
$$
Further, applying the cosine rule to triangles $A B D, A C D$ we get
$$
\begin{aligned}
A B^{2} & =B C^{2} / 4+A D^{2}-A D \cdot B C \cdot \cos \angle B D A, \\
A C^{2} & =B C^{2} / 4+A D^{2}+A D \cdot B C \cdot \cos \angle B D A, \\
\text { so } \quad A D^{2} & =\left(A B^{2}+A C^{2}-B C^{2} / 2\right) / 2
\end{aligned}
$$
Hence
$$
\begin{aligned}
\delta & =\left(A B^{2}+A C^{2}-2 B C^{2}\right) / 24 \\
& =\left(4 A B \cdot A C \cdot \cos \angle B A C-A B^{2}-A C^{2}\right)
\end{aligned}
$$
Now $A E F G$ is a cyclic quadrilateral if and only if $\delta=0$, i.e. if and only if
$$
\begin{aligned}
\cos \angle B A C & =\left(A B^{2}+A B^{2}\right) /(4 \cdot A B \cdot A C) \\
& =(A B / A C+A C / A B) / 4
\end{aligned}
$$
5
Now $A B / A C+A C / A B \geq 2$. Hence $\cos \angle B A C \geq 1 / 2$ and so $\angle B A C \leq 60^{\circ}$.
For $\angle B A C>60^{\circ}$ there is no triangle with the required property.
For $\angle B A C=60^{\circ}$ there exists, within similarity, precisely one triangle (which is equilateral) having the required property.
For $\angle B A C<60^{\circ}$ there exists, within similarity, again precisely one triangle having the required property (even though for fixed median $A E$ there are two, but one arises from the other by interchanging point $B$ with point $C$, thus proving them to be similar).
|
not found
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
In $\triangle A B C$, let $D, E, F$ be the midpoints of $B C, A C, A B$ respectively and let $G$ be the centroid of the triangle.
For each value of $\angle B A C$, how many non-similar triangles are there in which $A E G F$ is a cyclic quadrilateral?
|
Let $I$ be the intersection of $A G$ and $E F$.
Let $\delta=A I . I G-F I$ IE. Then
$$
A I=A D / 2, \quad I G=A D / 6, \quad F I=B C / 4=I E
$$
Further, applying the cosine rule to triangles $A B D, A C D$ we get
$$
\begin{aligned}
A B^{2} & =B C^{2} / 4+A D^{2}-A D \cdot B C \cdot \cos \angle B D A, \\
A C^{2} & =B C^{2} / 4+A D^{2}+A D \cdot B C \cdot \cos \angle B D A, \\
\text { so } \quad A D^{2} & =\left(A B^{2}+A C^{2}-B C^{2} / 2\right) / 2
\end{aligned}
$$
Hence
$$
\begin{aligned}
\delta & =\left(A B^{2}+A C^{2}-2 B C^{2}\right) / 24 \\
& =\left(4 A B \cdot A C \cdot \cos \angle B A C-A B^{2}-A C^{2}\right)
\end{aligned}
$$
Now $A E F G$ is a cyclic quadrilateral if and only if $\delta=0$, i.e. if and only if
$$
\begin{aligned}
\cos \angle B A C & =\left(A B^{2}+A B^{2}\right) /(4 \cdot A B \cdot A C) \\
& =(A B / A C+A C / A B) / 4
\end{aligned}
$$
5
Now $A B / A C+A C / A B \geq 2$. Hence $\cos \angle B A C \geq 1 / 2$ and so $\angle B A C \leq 60^{\circ}$.
For $\angle B A C>60^{\circ}$ there is no triangle with the required property.
For $\angle B A C=60^{\circ}$ there exists, within similarity, precisely one triangle (which is equilateral) having the required property.
For $\angle B A C<60^{\circ}$ there exists, within similarity, again precisely one triangle having the required property (even though for fixed median $A E$ there are two, but one arises from the other by interchanging point $B$ with point $C$, thus proving them to be similar).
|
{
"resource_path": "APMO/segmented/en-apmo1990_sol.jsonl",
"problem_match": "# Question 1 ",
"solution_match": "# FIRST SOLUTION\n\n"
}
|
72759d9d-1850-552c-805d-540717559e2c
| 604,224
|
In $\triangle A B C$, let $D, E, F$ be the midpoints of $B C, A C, A B$ respectively and let $G$ be the centroid of the triangle.
For each value of $\angle B A C$, how many non-similar triangles are there in which $A E G F$ is a cyclic quadrilateral?
|
(Mr Marcus Brazil, La Trobe University, Bundoora, Melbourne, Australia):
We require, as above,
$$
A I \cdot I G=E I \cdot I F
$$
(which by (1) is equivalent to $A D^{2} / 3=C D^{2}$, i.e. $A D=C D \cdot \sqrt{3}$ ).
Let, without loss of generality, $C D=1$. Then $A$ lies on the circle of radius $\sqrt{3}$ with centre $D$. If $C D$ and $D A$ are perpendicular, the angle $B A C$ is $60^{\circ}$, otherwise it must be less.
In this case, for each angle $B A C$ there are two solutions, which are congruent.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
In $\triangle A B C$, let $D, E, F$ be the midpoints of $B C, A C, A B$ respectively and let $G$ be the centroid of the triangle.
For each value of $\angle B A C$, how many non-similar triangles are there in which $A E G F$ is a cyclic quadrilateral?
|
(Mr Marcus Brazil, La Trobe University, Bundoora, Melbourne, Australia):
We require, as above,
$$
A I \cdot I G=E I \cdot I F
$$
(which by (1) is equivalent to $A D^{2} / 3=C D^{2}$, i.e. $A D=C D \cdot \sqrt{3}$ ).
Let, without loss of generality, $C D=1$. Then $A$ lies on the circle of radius $\sqrt{3}$ with centre $D$. If $C D$ and $D A$ are perpendicular, the angle $B A C$ is $60^{\circ}$, otherwise it must be less.
In this case, for each angle $B A C$ there are two solutions, which are congruent.
|
{
"resource_path": "APMO/segmented/en-apmo1990_sol.jsonl",
"problem_match": "# Question 1 ",
"solution_match": "\nSECOND SOLUTION "
}
|
72759d9d-1850-552c-805d-540717559e2c
| 604,224
|
In $\triangle A B C$, let $D, E, F$ be the midpoints of $B C, A C, A B$ respectively and let $G$ be the centroid of the triangle.
For each value of $\angle B A C$, how many non-similar triangles are there in which $A E G F$ is a cyclic quadrilateral?
|
in the figure as shown below, we first show that it is necessary that $\angle A$ is less than $90^{\circ}$ if the quadrilateral $A E G F$ ; cyclic.
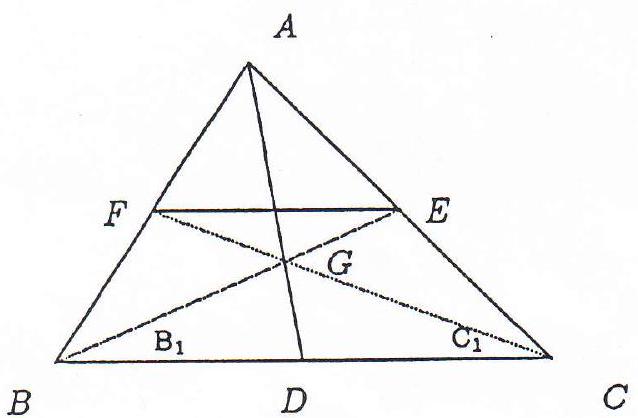
Now, since $E F \| B C$, we get
$$
\begin{aligned}
\angle E G F & =180^{\circ}-\left(B_{1}+C_{1}\right) \\
& \geq 180^{\circ}-(B+C) \\
& =A .
\end{aligned}
$$
(1)
Thus, if $A E G F$ is cyclic, we would have $\angle E G F+\angle A=180^{\circ}$. Therefore it is necessary that $0<\angle A \leq 90^{\circ}$.
## Continuation "A"
Let $O$ be the circumcentre of $\triangle A F E$. Without loss of generality, let the radius of this circle be 1.
We then let $A=1, F=z=e^{i \theta}$ and $E=z e^{2 i \alpha}=e^{i(\theta+2 \alpha)}$.
Then $\angle A=\alpha, 0<\alpha \leq 90^{\circ}$, and $0<\theta<360^{\circ}-2 \alpha$.
Thus,
$$
B=2 z-1
$$
and
$$
\begin{aligned}
G & =\frac{1}{3}(2 z-1)+\frac{2}{3}\left(z e^{2 i \alpha}\right) \\
& =\frac{1}{3}\left(2 e^{i \theta}+2 e^{i(\theta+2 \alpha)}-1\right)
\end{aligned}
$$
For quadrilateral $A F G E$ to be cyclic, it is now necessary that
$$
|G|=1 .
$$
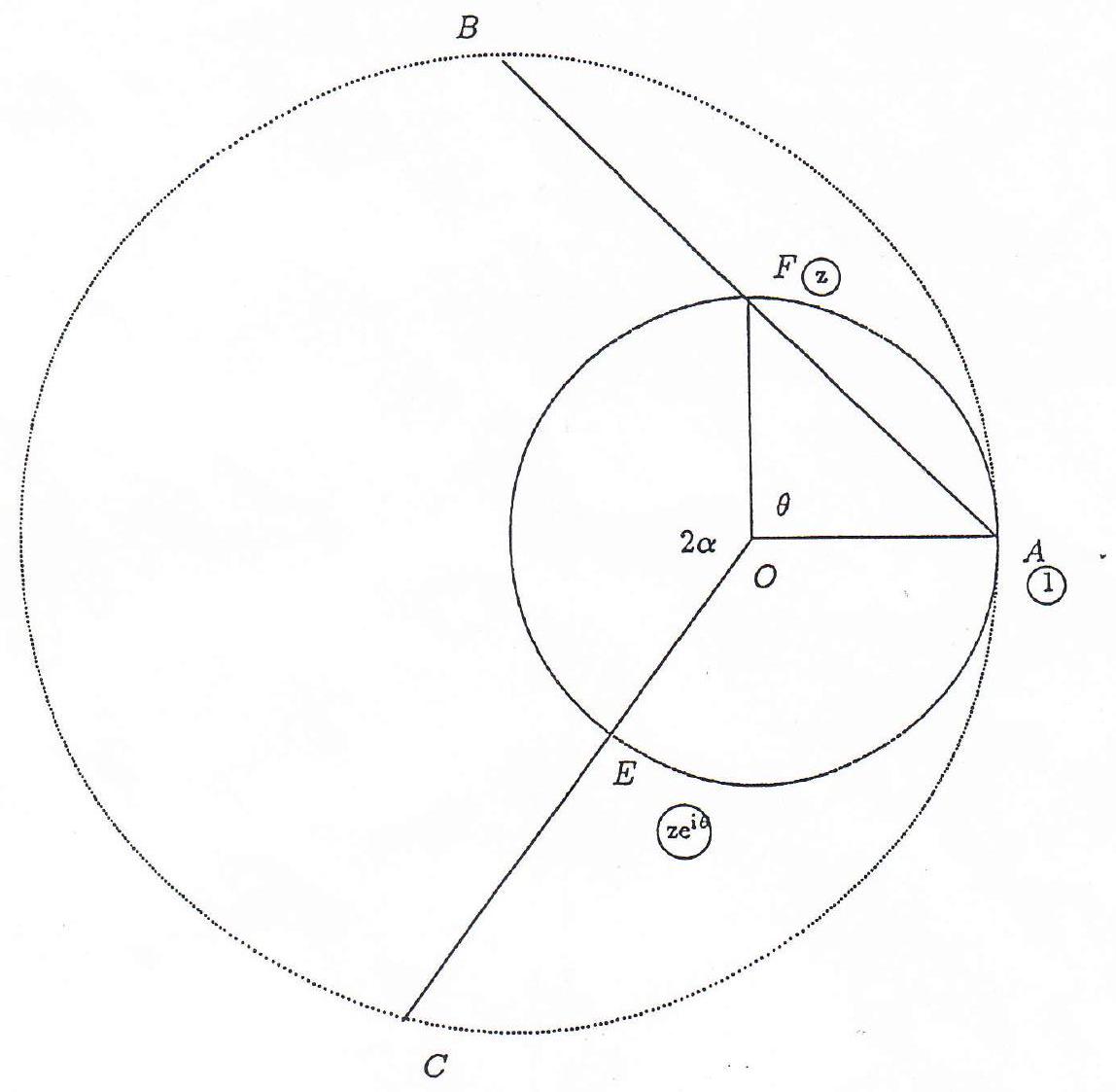
For $|G|=1$, we must have
$$
\begin{aligned}
9= & (2 \cos (\theta)+2 \cos (\theta+2 \alpha)-1)^{2}+(2 \sin (\theta)+2 \sin (\theta+2 \alpha))^{2} \\
= & 4\left(\cos ^{2}(\theta)+\sin ^{2}(\theta)\right)+4\left(\cos ^{2}(\theta+2 \alpha)+\sin ^{2}(\theta+2 \alpha)\right)+1 \\
& +8(\cos (\theta) \cos (\theta+2 \alpha)+\sin (\theta) \sin (\theta+2 \alpha))-4 \cos (\theta)-4 \cos (\theta+2 \alpha) \\
= & 9+8 \cos (2 \alpha)-8 \cos (\alpha) \cos (\theta+\alpha)
\end{aligned}
$$
so that
$$
\cos (\theta+\alpha)=\frac{\cos (2 \alpha)}{\cos (\alpha)}
$$
] Now, $\left|\frac{\cos (2 \alpha)}{\cos (\alpha)}\right| \leq 1$ if and only if $\alpha \in\left(0,60^{\circ}\right]$ in the range of $\alpha$ under consideration, that is $\alpha \in\left(0,00^{\circ}\right]$. There is equality if and only if $\alpha=60^{\circ}$.
$\square$ Note there is only one solution. The apparent other solution is the mirror image of the first. We are solving for $\alpha+\theta$. The other solution is $360^{\circ}-\alpha-\theta$.
## Continuation "B"
Let $O$ be the circumcentre of triangle $A E F$. Let $A P$ be a diameter of this circle. Construct the circle with centre $P$ and radius $A P$. Then $B$ and $C$ lie on this circle.
It is clear that the problem is solved if we allow the angle $\angle B A C=\alpha$ to vary and restrict $B$ and $C$ to the constructed circle.
Let $\theta$ be the angle from the drawn axis. Then $\theta$ lies in the range $\left(0,180^{\circ}-\alpha\right)$. We must not forget the necessary restriction of $\alpha$, that is $\alpha \in\left(0,90^{\circ}\right.$.
Now, $D$ lies on an arc of a circle, centre $P$, radius $P D$ exterior to the circle, centre $O$, radius $A O$.
By similarity, $G$, lies on an arc of a circle, centre $Q$, radius $Q G$ where $A Q=\frac{2}{3} A P$ and $Q G=\frac{2}{3} P D$.
For the quadrilateral $A F G E$ to be cyclic, we must have that the radius $Q G$ is greater than or equal to $Q P$.
The easiest way to calulate these radii is to consider the case in which the diameter $A P$ bisects the angle $\angle B A C$.
Thus we re-draw the diagram as below. Let $A H$ be a diameter of the larger circle.
Thus we have $A H=4$ and by similar triangles,
$$
\frac{A D}{A B}=\frac{A B}{A H}=\cos \left(\frac{\alpha}{2}\right)
$$
so that
$$
\begin{aligned}
A D & =4 \cos ^{2}\left(\frac{\alpha}{2}\right) \\
& =2+2 \cos (\alpha) .
\end{aligned}
$$
Thus $P D=2 \cos (\alpha)$ and $Q G=\frac{2}{3} 2 \cos (\alpha)=\frac{4}{3} \cos (\alpha)$.
The necessary condition for a cyclic quadrilateral is then
$$
\frac{4}{3}(1+\cos (\alpha)) \geq 2
$$
[5
$$
\cos (\alpha) \geq \frac{1}{2}
$$
:7
Thus it is clear that there is precisely one (up to similarity) solution for $0<\alpha \leq 60^{\circ}$ and no solutions otherwise.
|
0<\alpha \leq 60^{\circ}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
In $\triangle A B C$, let $D, E, F$ be the midpoints of $B C, A C, A B$ respectively and let $G$ be the centroid of the triangle.
For each value of $\angle B A C$, how many non-similar triangles are there in which $A E G F$ is a cyclic quadrilateral?
|
in the figure as shown below, we first show that it is necessary that $\angle A$ is less than $90^{\circ}$ if the quadrilateral $A E G F$ ; cyclic.

Now, since $E F \| B C$, we get
$$
\begin{aligned}
\angle E G F & =180^{\circ}-\left(B_{1}+C_{1}\right) \\
& \geq 180^{\circ}-(B+C) \\
& =A .
\end{aligned}
$$
(1)
Thus, if $A E G F$ is cyclic, we would have $\angle E G F+\angle A=180^{\circ}$. Therefore it is necessary that $0<\angle A \leq 90^{\circ}$.
## Continuation "A"
Let $O$ be the circumcentre of $\triangle A F E$. Without loss of generality, let the radius of this circle be 1.
We then let $A=1, F=z=e^{i \theta}$ and $E=z e^{2 i \alpha}=e^{i(\theta+2 \alpha)}$.
Then $\angle A=\alpha, 0<\alpha \leq 90^{\circ}$, and $0<\theta<360^{\circ}-2 \alpha$.
Thus,
$$
B=2 z-1
$$
and
$$
\begin{aligned}
G & =\frac{1}{3}(2 z-1)+\frac{2}{3}\left(z e^{2 i \alpha}\right) \\
& =\frac{1}{3}\left(2 e^{i \theta}+2 e^{i(\theta+2 \alpha)}-1\right)
\end{aligned}
$$
For quadrilateral $A F G E$ to be cyclic, it is now necessary that
$$
|G|=1 .
$$

For $|G|=1$, we must have
$$
\begin{aligned}
9= & (2 \cos (\theta)+2 \cos (\theta+2 \alpha)-1)^{2}+(2 \sin (\theta)+2 \sin (\theta+2 \alpha))^{2} \\
= & 4\left(\cos ^{2}(\theta)+\sin ^{2}(\theta)\right)+4\left(\cos ^{2}(\theta+2 \alpha)+\sin ^{2}(\theta+2 \alpha)\right)+1 \\
& +8(\cos (\theta) \cos (\theta+2 \alpha)+\sin (\theta) \sin (\theta+2 \alpha))-4 \cos (\theta)-4 \cos (\theta+2 \alpha) \\
= & 9+8 \cos (2 \alpha)-8 \cos (\alpha) \cos (\theta+\alpha)
\end{aligned}
$$
so that
$$
\cos (\theta+\alpha)=\frac{\cos (2 \alpha)}{\cos (\alpha)}
$$
] Now, $\left|\frac{\cos (2 \alpha)}{\cos (\alpha)}\right| \leq 1$ if and only if $\alpha \in\left(0,60^{\circ}\right]$ in the range of $\alpha$ under consideration, that is $\alpha \in\left(0,00^{\circ}\right]$. There is equality if and only if $\alpha=60^{\circ}$.

$\square$ Note there is only one solution. The apparent other solution is the mirror image of the first. We are solving for $\alpha+\theta$. The other solution is $360^{\circ}-\alpha-\theta$.
## Continuation "B"
Let $O$ be the circumcentre of triangle $A E F$. Let $A P$ be a diameter of this circle. Construct the circle with centre $P$ and radius $A P$. Then $B$ and $C$ lie on this circle.
It is clear that the problem is solved if we allow the angle $\angle B A C=\alpha$ to vary and restrict $B$ and $C$ to the constructed circle.
Let $\theta$ be the angle from the drawn axis. Then $\theta$ lies in the range $\left(0,180^{\circ}-\alpha\right)$. We must not forget the necessary restriction of $\alpha$, that is $\alpha \in\left(0,90^{\circ}\right.$.

Now, $D$ lies on an arc of a circle, centre $P$, radius $P D$ exterior to the circle, centre $O$, radius $A O$.
By similarity, $G$, lies on an arc of a circle, centre $Q$, radius $Q G$ where $A Q=\frac{2}{3} A P$ and $Q G=\frac{2}{3} P D$.
For the quadrilateral $A F G E$ to be cyclic, we must have that the radius $Q G$ is greater than or equal to $Q P$.
The easiest way to calulate these radii is to consider the case in which the diameter $A P$ bisects the angle $\angle B A C$.
Thus we re-draw the diagram as below. Let $A H$ be a diameter of the larger circle.

Thus we have $A H=4$ and by similar triangles,
$$
\frac{A D}{A B}=\frac{A B}{A H}=\cos \left(\frac{\alpha}{2}\right)
$$
so that
$$
\begin{aligned}
A D & =4 \cos ^{2}\left(\frac{\alpha}{2}\right) \\
& =2+2 \cos (\alpha) .
\end{aligned}
$$
Thus $P D=2 \cos (\alpha)$ and $Q G=\frac{2}{3} 2 \cos (\alpha)=\frac{4}{3} \cos (\alpha)$.
The necessary condition for a cyclic quadrilateral is then
$$
\frac{4}{3}(1+\cos (\alpha)) \geq 2
$$
[5
$$
\cos (\alpha) \geq \frac{1}{2}
$$
:7
Thus it is clear that there is precisely one (up to similarity) solution for $0<\alpha \leq 60^{\circ}$ and no solutions otherwise.
|
{
"resource_path": "APMO/segmented/en-apmo1990_sol.jsonl",
"problem_match": "# Question 1 ",
"solution_match": "\nTHIRD SOLUTION\n"
}
|
72759d9d-1850-552c-805d-540717559e2c
| 604,224
|
Let $a_{1}, a_{2}, \ldots, a_{n}$ be positive real numbers, and let $S_{k}$ be the sum of products of $a_{1}, a_{2}, \ldots, a_{n}$ taken $k$ at a time.
Show that
$$
S_{k} S_{n-k} \geq\binom{ n}{k}^{2} a_{1} a_{2} \ldots a_{n}, \quad \text { for } \quad k=1,2, \ldots, n-1
$$
|
$$
\binom{n}{k} a_{1} a_{2} \ldots a_{n}
$$
$2=\sum_{1 \leq i_{1}<i_{2}<\ldots<i_{k} \leq n} a_{i_{1}} a_{i_{2}} \ldots a_{i_{k}} \cdot a_{1} a_{2} \ldots a_{n} / a_{i_{1}} a_{i_{2}} \ldots a_{i_{k}}$
(and using the Cauchy-Schwarz inequality)
$$
\begin{aligned}
& \leq\left(\sum_{1 \leq i_{1}<i_{2}<\ldots<i_{k} \leq n} a_{i_{1}} a_{i_{2}} \ldots a_{i_{k}}\right)^{\frac{1}{2}} \cdot\left(\sum_{1 \leq i_{1}<i_{2}<\ldots<i_{k} \leq n} a_{1} a_{2} \ldots a_{n} / a_{i_{1}} a_{i_{2}} \ldots a_{i_{k}}\right)^{\frac{1}{2}} \\
& =S_{k}^{\frac{1}{2}} \cdot S_{n-k}^{\frac{1}{2}}
\end{aligned}
$$
Therefore
$$
\binom{n}{k}^{2} a_{1} a_{2} \ldots a_{n} \leq S_{k} S_{n-k}
$$
q.e.d.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a_{1}, a_{2}, \ldots, a_{n}$ be positive real numbers, and let $S_{k}$ be the sum of products of $a_{1}, a_{2}, \ldots, a_{n}$ taken $k$ at a time.
Show that
$$
S_{k} S_{n-k} \geq\binom{ n}{k}^{2} a_{1} a_{2} \ldots a_{n}, \quad \text { for } \quad k=1,2, \ldots, n-1
$$
|
$$
\binom{n}{k} a_{1} a_{2} \ldots a_{n}
$$
$2=\sum_{1 \leq i_{1}<i_{2}<\ldots<i_{k} \leq n} a_{i_{1}} a_{i_{2}} \ldots a_{i_{k}} \cdot a_{1} a_{2} \ldots a_{n} / a_{i_{1}} a_{i_{2}} \ldots a_{i_{k}}$
(and using the Cauchy-Schwarz inequality)
$$
\begin{aligned}
& \leq\left(\sum_{1 \leq i_{1}<i_{2}<\ldots<i_{k} \leq n} a_{i_{1}} a_{i_{2}} \ldots a_{i_{k}}\right)^{\frac{1}{2}} \cdot\left(\sum_{1 \leq i_{1}<i_{2}<\ldots<i_{k} \leq n} a_{1} a_{2} \ldots a_{n} / a_{i_{1}} a_{i_{2}} \ldots a_{i_{k}}\right)^{\frac{1}{2}} \\
& =S_{k}^{\frac{1}{2}} \cdot S_{n-k}^{\frac{1}{2}}
\end{aligned}
$$
Therefore
$$
\binom{n}{k}^{2} a_{1} a_{2} \ldots a_{n} \leq S_{k} S_{n-k}
$$
q.e.d.
|
{
"resource_path": "APMO/segmented/en-apmo1990_sol.jsonl",
"problem_match": "# Question 2",
"solution_match": "# FIRST SOLUTION\n\n"
}
|
92756af4-1c9d-52cf-ab66-3f4f0bc5e602
| 604,264
|
Let $a_{1}, a_{2}, \ldots, a_{n}$ be positive real numbers, and let $S_{k}$ be the sum of products of $a_{1}, a_{2}, \ldots, a_{n}$ taken $k$ at a time.
Show that
$$
S_{k} S_{n-k} \geq\binom{ n}{k}^{2} a_{1} a_{2} \ldots a_{n}, \quad \text { for } \quad k=1,2, \ldots, n-1
$$
|
(provided by the Canadian Problems Committee).
Write $S_{k}$ as $\sum_{i=1}^{\binom{n}{k}} t_{i}$. Then
주
$$
S_{n-k}=\left(\prod_{m=1}^{n} a_{m}\right)\left(\sum_{i=1}^{\binom{n}{k}} \frac{1}{t_{i}}\right)
$$
$$
\text { so that } \left.\begin{array}{rl}
S_{k} S_{n-k} & =\left(\prod_{m=1}^{n} a_{m}\right) \cdot\left(\begin{array}{l}
\binom{n}{k} \\
i=1
\end{array} t_{i}\right)\left(\begin{array}{l}
\binom{n}{k} \\
\sum_{j=1}^{2}
\end{array} \frac{1}{t_{j}}\right) \\
& =\left(\prod_{m=1}^{n} a_{m}\right)\left[\sum_{i=1}^{\binom{n}{k}} 1+\sum_{i=1}^{\binom{n}{k}} \sum_{j=1}^{n} \begin{array}{l}
n \\
k
\end{array}\right) \\
\frac{t_{i}}{} \\
t_{j}
\end{array}\right] .
$$
As there are
$$
\frac{\binom{n}{k}^{2}-\binom{n}{k}}{2}
$$
terms in the sum

$$
\begin{aligned}
S_{k} S_{n-k} & \geq\left(\prod_{m=1}^{n} a_{m}\right)\left[\binom{n}{k}+2 \cdot \frac{\binom{n}{k}^{2}-\binom{n}{k}}{2}\right] \\
& =\binom{n}{k}^{2}\left(\prod_{m=1}^{n} a_{m}\right)
\end{aligned}
$$
since $\frac{t_{i}}{t_{j}}+\frac{t_{j}}{t_{i}} \geq 2$ for $t_{i}, t_{j}>0$.
|
proof
|
Yes
|
Incomplete
|
proof
|
Inequalities
|
Let $a_{1}, a_{2}, \ldots, a_{n}$ be positive real numbers, and let $S_{k}$ be the sum of products of $a_{1}, a_{2}, \ldots, a_{n}$ taken $k$ at a time.
Show that
$$
S_{k} S_{n-k} \geq\binom{ n}{k}^{2} a_{1} a_{2} \ldots a_{n}, \quad \text { for } \quad k=1,2, \ldots, n-1
$$
|
(provided by the Canadian Problems Committee).
Write $S_{k}$ as $\sum_{i=1}^{\binom{n}{k}} t_{i}$. Then
주
$$
S_{n-k}=\left(\prod_{m=1}^{n} a_{m}\right)\left(\sum_{i=1}^{\binom{n}{k}} \frac{1}{t_{i}}\right)
$$
$$
\text { so that } \left.\begin{array}{rl}
S_{k} S_{n-k} & =\left(\prod_{m=1}^{n} a_{m}\right) \cdot\left(\begin{array}{l}
\binom{n}{k} \\
i=1
\end{array} t_{i}\right)\left(\begin{array}{l}
\binom{n}{k} \\
\sum_{j=1}^{2}
\end{array} \frac{1}{t_{j}}\right) \\
& =\left(\prod_{m=1}^{n} a_{m}\right)\left[\sum_{i=1}^{\binom{n}{k}} 1+\sum_{i=1}^{\binom{n}{k}} \sum_{j=1}^{n} \begin{array}{l}
n \\
k
\end{array}\right) \\
\frac{t_{i}}{} \\
t_{j}
\end{array}\right] .
$$
As there are
$$
\frac{\binom{n}{k}^{2}-\binom{n}{k}}{2}
$$
terms in the sum

$$
\begin{aligned}
S_{k} S_{n-k} & \geq\left(\prod_{m=1}^{n} a_{m}\right)\left[\binom{n}{k}+2 \cdot \frac{\binom{n}{k}^{2}-\binom{n}{k}}{2}\right] \\
& =\binom{n}{k}^{2}\left(\prod_{m=1}^{n} a_{m}\right)
\end{aligned}
$$
since $\frac{t_{i}}{t_{j}}+\frac{t_{j}}{t_{i}} \geq 2$ for $t_{i}, t_{j}>0$.
|
{
"resource_path": "APMO/segmented/en-apmo1990_sol.jsonl",
"problem_match": "# Question 2",
"solution_match": "\nSECOND SOLUTION "
}
|
92756af4-1c9d-52cf-ab66-3f4f0bc5e602
| 604,264
|
Consider all the triangles $A B C$ which have a fixed base $A B$ and whose altitude from $C$ is a constant $h$. For which of these triangles is the product of its altitudes a maximum?
|
Let $h_{a}$ and $h_{b}$ be the altitudes from $A$ and $B$, respectively. Then
$$
\begin{aligned}
A B \cdot h \cdot A C \cdot h_{b} \cdot B C \cdot h_{a} & =8 . \text { area of } \triangle A B C)^{3} \\
& =(A B \cdot h)^{3},
\end{aligned}
$$
园
which is a constant. So the product $h . h_{a} \cdot h_{b}$ attains its maximum when the product $A C . B C$ attains its minimum.
Since
$$
\begin{aligned}
(\sin C) \cdot A C \cdot B C & =B C \cdot h_{a} \\
& =2 \cdot \text { area of } \triangle A B C
\end{aligned}
$$
(3)
which is a constant, $A C \cdot B C$ attains its minimum when $\sin C$ reaches its maximum. There are two cases:
(a) $h \leq A B / 2$. Then there exists a triangle $A B C$ which has a right angle at $C$, and for precisely such a triangle $\sin C$ attains its maximum, namely 1 .
(b) $h>A B / 2$. In this case the angle at $C$ is acute and assumes its maximum when the triangle is isosceles.
Note that a solution using calculus obviously exists.
|
not found
|
Yes
|
Incomplete
|
math-word-problem
|
Geometry
|
Consider all the triangles $A B C$ which have a fixed base $A B$ and whose altitude from $C$ is a constant $h$. For which of these triangles is the product of its altitudes a maximum?
|
Let $h_{a}$ and $h_{b}$ be the altitudes from $A$ and $B$, respectively. Then
$$
\begin{aligned}
A B \cdot h \cdot A C \cdot h_{b} \cdot B C \cdot h_{a} & =8 . \text { area of } \triangle A B C)^{3} \\
& =(A B \cdot h)^{3},
\end{aligned}
$$
园
which is a constant. So the product $h . h_{a} \cdot h_{b}$ attains its maximum when the product $A C . B C$ attains its minimum.
Since
$$
\begin{aligned}
(\sin C) \cdot A C \cdot B C & =B C \cdot h_{a} \\
& =2 \cdot \text { area of } \triangle A B C
\end{aligned}
$$
(3)
which is a constant, $A C \cdot B C$ attains its minimum when $\sin C$ reaches its maximum. There are two cases:
(a) $h \leq A B / 2$. Then there exists a triangle $A B C$ which has a right angle at $C$, and for precisely such a triangle $\sin C$ attains its maximum, namely 1 .
(b) $h>A B / 2$. In this case the angle at $C$ is acute and assumes its maximum when the triangle is isosceles.
Note that a solution using calculus obviously exists.
|
{
"resource_path": "APMO/segmented/en-apmo1990_sol.jsonl",
"problem_match": "# Question 3",
"solution_match": "# SOLUTION:"
}
|
b1c671c1-7a4b-5875-8c4a-600c99bedcd8
| 604,287
|
A set of 1990 persons is divided into non-intersecting subsets in such a way that
(a) no one in a subset knows all the others in the subset;
(b) among any three persons in a subset, there are always at least two who do not know each other; and
(c) for any two persons in a subset who do not know each other, there is exactly one person in the same subset knowing both of them.
(i) Prove that within each subset, every person has the same number of acquaintances.
(ii) Determine the maximum possible number of subsets.
Note: it is understood that if a person $A$ knows person $B$, then person $B$ will know person $A$; an acquaintance is someone who is known. Every person is assumed to know one's self.
|
(i) Let $S$ be a subset of persons satisfying conditions (a), (b) and (c). Let $x \in S$ be one who knows the maximum number of persons in $S$.
Assume that $x$ knows $x_{1}, x_{2}, \ldots, x_{n}$. By (b), $x_{i}$ and $x_{j}$ are strangers if $i \neq j$. For each $x_{i}$, let $N_{i}$ be the set of persons in $S$ who know $x_{i}$ but not $x$. Note that, for $i \neq j, N_{i}$ has no person in common with $N_{j}$, otherwise there would be more than one person knowing $x_{i}$ and $x_{j}$, contradicting (c).
By (a) we may assume that $N_{1}$ is not empty.) Let $y_{1} \in N_{1}$. By (c), for each $k>1$, there is exactly one person $y_{k}$ in $N_{k}$ who knows $y_{1}$. This means that $y_{1}$ knows $n$ persons, namely $x_{1}, y_{2}, \ldots, y_{n}$.
Because $n$ is the maximal number of persons in $S$ a person in $S$ can know, $y_{1}$ knows exactly $n$ persons in $S$. By precisely the same reasoning we find that each person in $N_{i}$, $i=1,2, \ldots, n$, knows exactly $n$ persons in $S$.
Letting $y_{1}$ take the role of $x$ in our argument, we see that also each $x_{i}$ knows exactly $n$ persons. Note that, by (c), every person in $S$ other than $x, x_{1}, \ldots, x_{n}$, must be in some $N_{j}$. Therefore every person in $S$ knows exactly $n$ persons in $S$ and thus has the same number of acquaintances in $S$.
(ii) To maximize the number of subsets, we have to minimize the size of each group. The smallest possible subset is one in which every person knows exactly two persons, and hence there must be exactly five persons in the subset, forming a cycle where two persons stand side by side only if they know each other. Therefore the maximum possible number of subsets is 1990/5 $=398$.
|
398
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A set of 1990 persons is divided into non-intersecting subsets in such a way that
(a) no one in a subset knows all the others in the subset;
(b) among any three persons in a subset, there are always at least two who do not know each other; and
(c) for any two persons in a subset who do not know each other, there is exactly one person in the same subset knowing both of them.
(i) Prove that within each subset, every person has the same number of acquaintances.
(ii) Determine the maximum possible number of subsets.
Note: it is understood that if a person $A$ knows person $B$, then person $B$ will know person $A$; an acquaintance is someone who is known. Every person is assumed to know one's self.
|
(i) Let $S$ be a subset of persons satisfying conditions (a), (b) and (c). Let $x \in S$ be one who knows the maximum number of persons in $S$.
Assume that $x$ knows $x_{1}, x_{2}, \ldots, x_{n}$. By (b), $x_{i}$ and $x_{j}$ are strangers if $i \neq j$. For each $x_{i}$, let $N_{i}$ be the set of persons in $S$ who know $x_{i}$ but not $x$. Note that, for $i \neq j, N_{i}$ has no person in common with $N_{j}$, otherwise there would be more than one person knowing $x_{i}$ and $x_{j}$, contradicting (c).
By (a) we may assume that $N_{1}$ is not empty.) Let $y_{1} \in N_{1}$. By (c), for each $k>1$, there is exactly one person $y_{k}$ in $N_{k}$ who knows $y_{1}$. This means that $y_{1}$ knows $n$ persons, namely $x_{1}, y_{2}, \ldots, y_{n}$.
Because $n$ is the maximal number of persons in $S$ a person in $S$ can know, $y_{1}$ knows exactly $n$ persons in $S$. By precisely the same reasoning we find that each person in $N_{i}$, $i=1,2, \ldots, n$, knows exactly $n$ persons in $S$.
Letting $y_{1}$ take the role of $x$ in our argument, we see that also each $x_{i}$ knows exactly $n$ persons. Note that, by (c), every person in $S$ other than $x, x_{1}, \ldots, x_{n}$, must be in some $N_{j}$. Therefore every person in $S$ knows exactly $n$ persons in $S$ and thus has the same number of acquaintances in $S$.
(ii) To maximize the number of subsets, we have to minimize the size of each group. The smallest possible subset is one in which every person knows exactly two persons, and hence there must be exactly five persons in the subset, forming a cycle where two persons stand side by side only if they know each other. Therefore the maximum possible number of subsets is 1990/5 $=398$.
|
{
"resource_path": "APMO/segmented/en-apmo1990_sol.jsonl",
"problem_match": "# Question 4",
"solution_match": "# SOLUTION:"
}
|
97a76adf-0b62-5330-a551-d2887bfc31ee
| 604,299
|
Show that for every integer $n \geq 6$, there exists a convex hexagon which can be dissected into exactly $n$ congruent triangles.
|
(provided by the Canadian Problems Committee).
The basic building blocks will be right angled triangles with sides $p, q$ (which are positive integers) adjacent to the right angle.
In the first instance, we take $p=q=1$ and construct five basic building blocks: $L_{1}, L_{2}, M, R_{1}$ and $R_{2}$ 。
## [3)
$L_{1}$
$L_{2}$
M
$R_{1}$
$R_{2}$
We shall now build convex hexagons by taking, on the left, one of the blocks $L_{i}$, attaching $n$ copies of the block $M$, and finally attaching one of the blocks $R_{j}$. We must therefore exclude the case when $(i, j)=(2,1)$ for this does not generate a hexagon. Further, for $(i, j)=(1,1)$ or $(i, j)=(1,2)$, we require that $n \geq 1$, whereas for $(i, j)=$ $(2,2)$, we only need require that $n \geq 0$.
Thus, with the obvious interpretation:
$L_{1}+n M+R_{1}$ gives a convex hexagon containing $2+4 n+2=4 n+4 \quad(n \geq 1)$ congruent triangles;
$L_{1}+n M+R_{2}$ gives a convex hexagon containing $2+4 n+3=4 n+5(n \geq 1)$ congruent triangles; and
$L_{2}+n M+R_{2}$ gives a convex hexagon containing $3+4 n+3=4 n+6 \quad(n \geq 0)$ congruent triangles, or $4 n+2(n \geq 1)$ congruent triangles.
We shall now modify the lengths of the sides of the right triangle to obtain the case of $4 n+3 \quad(n \geq 1)$ congruent triangles.
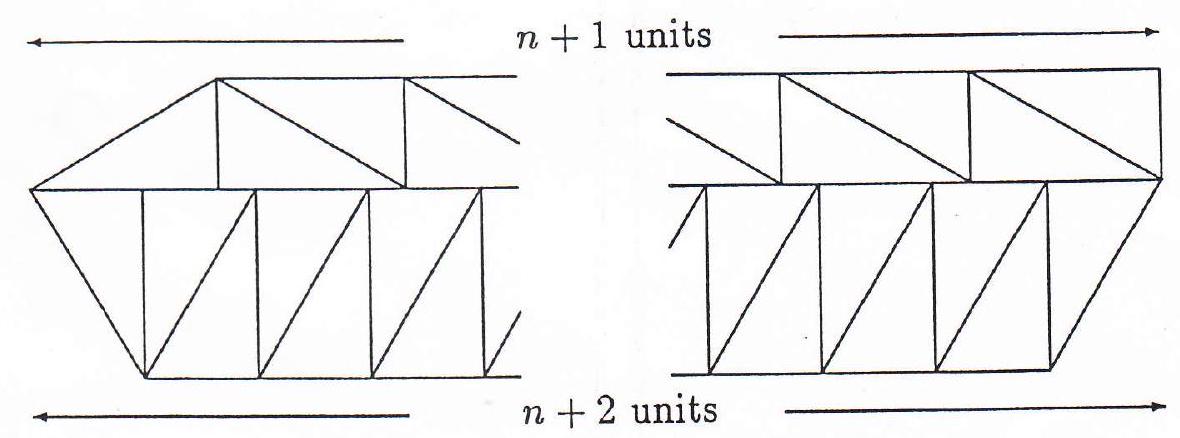
So we have $2 n+1$ triangles in the top part and $2 n+2$ triangles in the bottom part. In order to match, we need
$$
(n+1) p=(n+2) q
$$
so we take
$$
q=n+1 \quad \text { and } \quad p=n+2
$$
This completes the solution.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Show that for every integer $n \geq 6$, there exists a convex hexagon which can be dissected into exactly $n$ congruent triangles.
|
(provided by the Canadian Problems Committee).
The basic building blocks will be right angled triangles with sides $p, q$ (which are positive integers) adjacent to the right angle.
In the first instance, we take $p=q=1$ and construct five basic building blocks: $L_{1}, L_{2}, M, R_{1}$ and $R_{2}$ 。
## [3)

$L_{1}$

$L_{2}$

M

$R_{1}$

$R_{2}$
We shall now build convex hexagons by taking, on the left, one of the blocks $L_{i}$, attaching $n$ copies of the block $M$, and finally attaching one of the blocks $R_{j}$. We must therefore exclude the case when $(i, j)=(2,1)$ for this does not generate a hexagon. Further, for $(i, j)=(1,1)$ or $(i, j)=(1,2)$, we require that $n \geq 1$, whereas for $(i, j)=$ $(2,2)$, we only need require that $n \geq 0$.
Thus, with the obvious interpretation:
$L_{1}+n M+R_{1}$ gives a convex hexagon containing $2+4 n+2=4 n+4 \quad(n \geq 1)$ congruent triangles;
$L_{1}+n M+R_{2}$ gives a convex hexagon containing $2+4 n+3=4 n+5(n \geq 1)$ congruent triangles; and
$L_{2}+n M+R_{2}$ gives a convex hexagon containing $3+4 n+3=4 n+6 \quad(n \geq 0)$ congruent triangles, or $4 n+2(n \geq 1)$ congruent triangles.
We shall now modify the lengths of the sides of the right triangle to obtain the case of $4 n+3 \quad(n \geq 1)$ congruent triangles.

So we have $2 n+1$ triangles in the top part and $2 n+2$ triangles in the bottom part. In order to match, we need
$$
(n+1) p=(n+2) q
$$
so we take
$$
q=n+1 \quad \text { and } \quad p=n+2
$$
This completes the solution.
|
{
"resource_path": "APMO/segmented/en-apmo1990_sol.jsonl",
"problem_match": "# Question 5",
"solution_match": "\nFIRST SOLUTION "
}
|
73c9ec95-e9ca-5aef-bf23-74672775d15a
| 54,403
|
Show that for every integer $n \geq 6$, there exists a convex hexagon which can be dissected into exactly $n$ congruent triangles.
|
(provided by the Canadian Problems Committee):
The basic building blocks will be right angled triangles with sides $m, n$ (which are positive integers) adjacent to the right angle.
We construct an "UPPER CONFIGURATION", being a rectangle consisting of $m$ building block units of pairs of triangles with the side of length $n$ as base. This gives a base length of $n m$ across the configuration.
We further construct a "LOWER CONFIGURATION", being a triangle with base up, consisting along the base of $n$ building block units. Again, we have a base length of $m n$ across the configuration.
Two triangles in the upper configuration are shaded horizontally. One triangle in the lower configuration is also shaded horizontally. Another triangle in the lower configuration is shaded vertically.
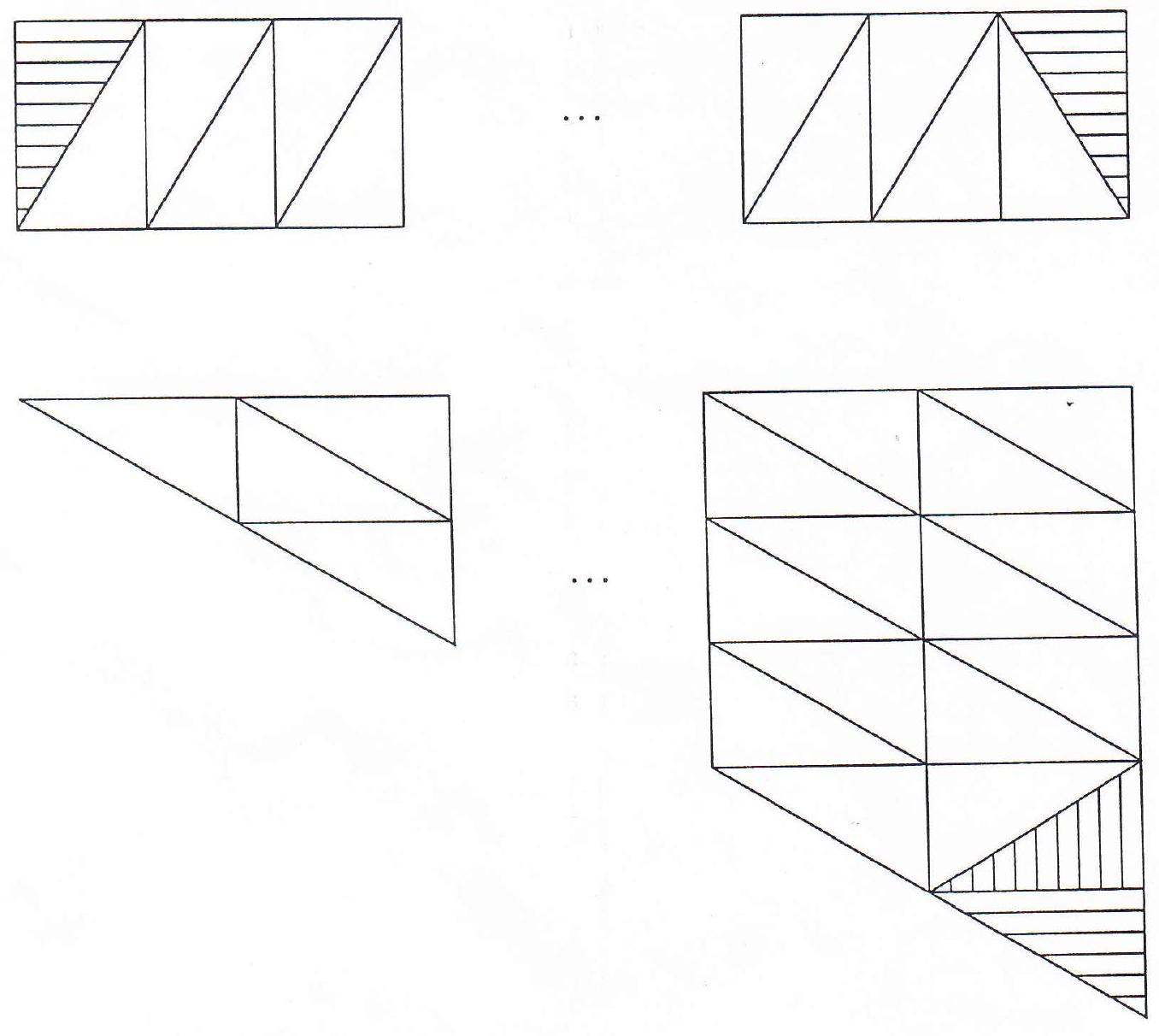
Now consider the figure obtained by joining the two configurations along the base line of common length nm. To create the classes of hexagons defined below, it is necessary that both $n \geq 3$ and $m \geq 3$.
We create a class of convex hexagons (class 1 ) by omitting the three triangles that are shaded horizontally. The other class of convex hexagons (class 2) is obtained by omitting all shaded triangles.
Now count the total number of triangles in the full configuration.
The upper configuration gives $2 m$ triangles. The lower configuration gives
$$
\sum_{k=1}^{n}(2 k-1)=n^{2} \quad \text { triangles. }
$$
Thus the total number of triangles in a hexagon in class 1 is
$$
2 m-2+n^{2}-1
$$
and the total number of triangle in a hexagon in class 2 is
$$
2 m-2+n^{2}-2
$$
These, together with the restrictions on $n$ and $m$, generate all positive integers greater than or equal to 11.
For the integers $6,7,8,9$ and 10 , we give specific examples:
6
7
8
9
10
This completes the solution.
There are $\binom{n}{k}$ products of the $a_{i}$ taken $k$ at a time. Amongst these products any given $a_{i}$ will appear $\binom{n-1}{k-1}$ times, since $\binom{n-1}{k-1}$ is the number of ways of choosing the other factors of the product. So the $\mathrm{AM} / \mathrm{GM}$ inequality gives
## ④
$$
\frac{S_{k}}{\binom{n}{k}} \geq\left[\prod_{i=1}^{n} a_{i}^{\binom{n-1}{k-1}}\right]^{\frac{1}{n}\binom{n}{n}}
$$
But $\binom{n}{k}=\frac{n}{k}\binom{n-1}{k-1}$, leading to
6 S $\quad S_{k} \geq\binom{ n}{k}\left(\prod_{i=1}^{n} a_{i}\right)^{\frac{k}{n}}$.
Hence
田
$$
S_{k} S_{n-k} \geq\binom{ n}{k}\left(\prod_{i=1}^{n} a_{i}\right)^{\frac{k}{n}}\binom{n}{n-k}\left(\prod_{i=1}^{n} a_{i}\right)^{\frac{n-k}{n}}=\binom{n}{k}^{2}\left(\prod_{1}^{n} a_{i}\right) .
$$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Show that for every integer $n \geq 6$, there exists a convex hexagon which can be dissected into exactly $n$ congruent triangles.
|
(provided by the Canadian Problems Committee):
The basic building blocks will be right angled triangles with sides $m, n$ (which are positive integers) adjacent to the right angle.

We construct an "UPPER CONFIGURATION", being a rectangle consisting of $m$ building block units of pairs of triangles with the side of length $n$ as base. This gives a base length of $n m$ across the configuration.
We further construct a "LOWER CONFIGURATION", being a triangle with base up, consisting along the base of $n$ building block units. Again, we have a base length of $m n$ across the configuration.
Two triangles in the upper configuration are shaded horizontally. One triangle in the lower configuration is also shaded horizontally. Another triangle in the lower configuration is shaded vertically.

Now consider the figure obtained by joining the two configurations along the base line of common length nm. To create the classes of hexagons defined below, it is necessary that both $n \geq 3$ and $m \geq 3$.
We create a class of convex hexagons (class 1 ) by omitting the three triangles that are shaded horizontally. The other class of convex hexagons (class 2) is obtained by omitting all shaded triangles.
Now count the total number of triangles in the full configuration.
The upper configuration gives $2 m$ triangles. The lower configuration gives
$$
\sum_{k=1}^{n}(2 k-1)=n^{2} \quad \text { triangles. }
$$
Thus the total number of triangles in a hexagon in class 1 is
$$
2 m-2+n^{2}-1
$$
and the total number of triangle in a hexagon in class 2 is
$$
2 m-2+n^{2}-2
$$
These, together with the restrictions on $n$ and $m$, generate all positive integers greater than or equal to 11.
For the integers $6,7,8,9$ and 10 , we give specific examples:

6

7

8

9

10
This completes the solution.
There are $\binom{n}{k}$ products of the $a_{i}$ taken $k$ at a time. Amongst these products any given $a_{i}$ will appear $\binom{n-1}{k-1}$ times, since $\binom{n-1}{k-1}$ is the number of ways of choosing the other factors of the product. So the $\mathrm{AM} / \mathrm{GM}$ inequality gives
## ④
$$
\frac{S_{k}}{\binom{n}{k}} \geq\left[\prod_{i=1}^{n} a_{i}^{\binom{n-1}{k-1}}\right]^{\frac{1}{n}\binom{n}{n}}
$$
But $\binom{n}{k}=\frac{n}{k}\binom{n-1}{k-1}$, leading to
6 S $\quad S_{k} \geq\binom{ n}{k}\left(\prod_{i=1}^{n} a_{i}\right)^{\frac{k}{n}}$.
Hence
田
$$
S_{k} S_{n-k} \geq\binom{ n}{k}\left(\prod_{i=1}^{n} a_{i}\right)^{\frac{k}{n}}\binom{n}{n-k}\left(\prod_{i=1}^{n} a_{i}\right)^{\frac{n-k}{n}}=\binom{n}{k}^{2}\left(\prod_{1}^{n} a_{i}\right) .
$$
|
{
"resource_path": "APMO/segmented/en-apmo1990_sol.jsonl",
"problem_match": "# Question 5",
"solution_match": "\nSECOND SOLUTION "
}
|
73c9ec95-e9ca-5aef-bf23-74672775d15a
| 54,403
|
Let $G$ be the centroid of triangle $A B C$ and $M$ be the midpoint of $B C$. Let $X$ be on $A B$ and $Y$ on $A C$ such that the points $X, Y$, and $G$ are collinear and $X Y$ and $B C$ are parallel. Suppose that $X C$ and $G B$ intersect at $Q$ and $Y B$ and $G C$ intersect at $P$. Show that triangle $M P Q$ is similar to triangle $A B C$.
|
Let $R$ be the midpoint of $A C$; so $B R$ is a median and contains the centroid $G$.
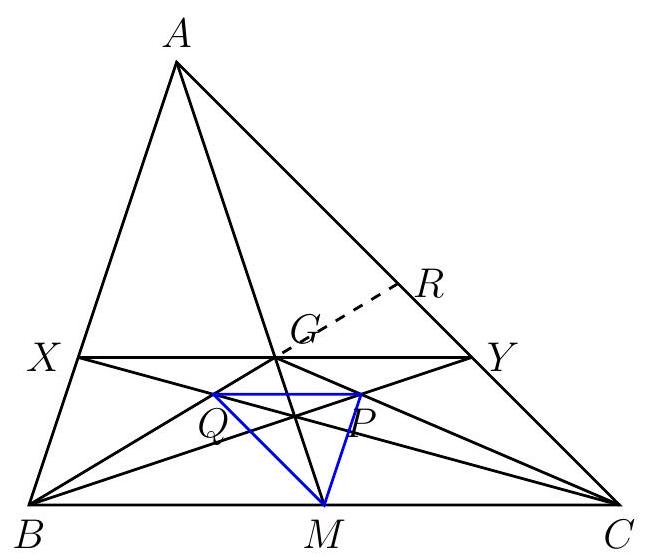
It is well known that $\frac{A G}{A M}=\frac{2}{3}$; thus the ratio of the similarity between $A X Y$ and $A B C$ is $\frac{2}{3}$. Hence $G X=\frac{1}{2} X Y=\frac{1}{3} B C$.
Now look at the similarity between triangles $Q B C$ and $Q G X$ :
$$
\frac{Q G}{Q B}=\frac{G X}{B C}=\frac{1}{3} \Longrightarrow Q B=3 Q G \Longrightarrow Q B=\frac{3}{4} B G=\frac{3}{4} \cdot \frac{2}{3} B R=\frac{1}{2} B R .
$$
Finally, since $\frac{B M}{B C}=\frac{B Q}{B R}, M Q$ is a midline in $B C R$. Therefore $M Q=\frac{1}{2} C R=\frac{1}{4} A C$ and $M Q \| A C$. Similarly, $M P=\frac{1}{4} A B$ and $M P \| A B$. This is sufficient to establish that $M P Q$ and $A B C$ are similar (with similarity ratio $\frac{1}{4}$ ).
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $G$ be the centroid of triangle $A B C$ and $M$ be the midpoint of $B C$. Let $X$ be on $A B$ and $Y$ on $A C$ such that the points $X, Y$, and $G$ are collinear and $X Y$ and $B C$ are parallel. Suppose that $X C$ and $G B$ intersect at $Q$ and $Y B$ and $G C$ intersect at $P$. Show that triangle $M P Q$ is similar to triangle $A B C$.
|
Let $R$ be the midpoint of $A C$; so $B R$ is a median and contains the centroid $G$.

It is well known that $\frac{A G}{A M}=\frac{2}{3}$; thus the ratio of the similarity between $A X Y$ and $A B C$ is $\frac{2}{3}$. Hence $G X=\frac{1}{2} X Y=\frac{1}{3} B C$.
Now look at the similarity between triangles $Q B C$ and $Q G X$ :
$$
\frac{Q G}{Q B}=\frac{G X}{B C}=\frac{1}{3} \Longrightarrow Q B=3 Q G \Longrightarrow Q B=\frac{3}{4} B G=\frac{3}{4} \cdot \frac{2}{3} B R=\frac{1}{2} B R .
$$
Finally, since $\frac{B M}{B C}=\frac{B Q}{B R}, M Q$ is a midline in $B C R$. Therefore $M Q=\frac{1}{2} C R=\frac{1}{4} A C$ and $M Q \| A C$. Similarly, $M P=\frac{1}{4} A B$ and $M P \| A B$. This is sufficient to establish that $M P Q$ and $A B C$ are similar (with similarity ratio $\frac{1}{4}$ ).
|
{
"resource_path": "APMO/segmented/en-apmo1991_sol.jsonl",
"problem_match": "# Problem 1",
"solution_match": "# Solution 1"
}
|
bd1d8513-fe5c-50c2-a9d8-0c6ddc4272c9
| 604,343
|
Let $G$ be the centroid of triangle $A B C$ and $M$ be the midpoint of $B C$. Let $X$ be on $A B$ and $Y$ on $A C$ such that the points $X, Y$, and $G$ are collinear and $X Y$ and $B C$ are parallel. Suppose that $X C$ and $G B$ intersect at $Q$ and $Y B$ and $G C$ intersect at $P$. Show that triangle $M P Q$ is similar to triangle $A B C$.
|
Let $S$ and $R$ be the midpoints of $A B$ and $A C$, respectively. Since $G$ is the centroid, it lies in the medians $B R$ and $C S$.
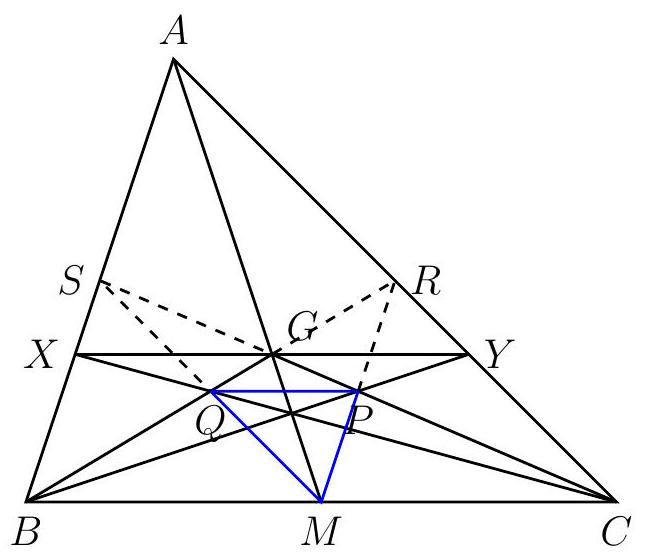
Due to the similarity between triangles $Q B C$ and $Q G X$ (which is true because $G X \| B C$ ), there is an inverse homothety with center $Q$ and ratio $-\frac{X G}{B C}=\frac{X Y}{2 B C}$ that takes $B$ to $G$ and $C$ to $X$. This homothety takes the midpoint $M$ of $B C$ to the midpoint $K$ of $G X$.
Now consider the homothety that takes $B$ to $X$ and $C$ to $G$. This new homothety, with ratio $\frac{X Y}{2 B C}$, also takes $M$ to $K$. Hence lines $B X$ (which contains side $A B$ ), $C G$ (which contains the median $C S$ ), and $M K$ have a common point, which is $S$. Thus $Q$ lies on midline $M S$.
The same reasoning proves that $P$ lies on midline $M R$. Since all homothety ratios are the same, $\frac{M Q}{M S}=\frac{M P}{M R}$, which shows that $M P Q$ is similar to $M R S$, which in turn is similar to $A B C$, and we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $G$ be the centroid of triangle $A B C$ and $M$ be the midpoint of $B C$. Let $X$ be on $A B$ and $Y$ on $A C$ such that the points $X, Y$, and $G$ are collinear and $X Y$ and $B C$ are parallel. Suppose that $X C$ and $G B$ intersect at $Q$ and $Y B$ and $G C$ intersect at $P$. Show that triangle $M P Q$ is similar to triangle $A B C$.
|
Let $S$ and $R$ be the midpoints of $A B$ and $A C$, respectively. Since $G$ is the centroid, it lies in the medians $B R$ and $C S$.

Due to the similarity between triangles $Q B C$ and $Q G X$ (which is true because $G X \| B C$ ), there is an inverse homothety with center $Q$ and ratio $-\frac{X G}{B C}=\frac{X Y}{2 B C}$ that takes $B$ to $G$ and $C$ to $X$. This homothety takes the midpoint $M$ of $B C$ to the midpoint $K$ of $G X$.
Now consider the homothety that takes $B$ to $X$ and $C$ to $G$. This new homothety, with ratio $\frac{X Y}{2 B C}$, also takes $M$ to $K$. Hence lines $B X$ (which contains side $A B$ ), $C G$ (which contains the median $C S$ ), and $M K$ have a common point, which is $S$. Thus $Q$ lies on midline $M S$.
The same reasoning proves that $P$ lies on midline $M R$. Since all homothety ratios are the same, $\frac{M Q}{M S}=\frac{M P}{M R}$, which shows that $M P Q$ is similar to $M R S$, which in turn is similar to $A B C$, and we are done.
|
{
"resource_path": "APMO/segmented/en-apmo1991_sol.jsonl",
"problem_match": "# Problem 1",
"solution_match": "# Solution 2"
}
|
bd1d8513-fe5c-50c2-a9d8-0c6ddc4272c9
| 604,343
|
Suppose there are 997 points given in a plane. If every two points are joined by a line segment with its midpoint coloured in red, show that there are at least 1991 red points in the plane. Can you find a special case with exactly 1991 red points?
|
Embed the points in the cartesian plane such that no two points have the same $y$-coordinate. Let $P_{1}, P_{2}, \ldots, P_{997}$ be the points and $y_{1}<y_{2}<\ldots<y_{997}$ be their respective $y$-coordinates. Then the $y$-coordinate of the midpoint of $P_{i} P_{i+1}, i=1,2, \ldots, 996$ is $\frac{y_{i}+y_{i+1}}{2}$ and the $y$-coordinate of the midpoint of $P_{i} P_{i+2}, i=1,2, \ldots, 995$ is $\frac{y_{i}+y_{i+2}}{2}$. Since
$$
\frac{y_{1}+y_{2}}{2}<\frac{y_{1}+y_{3}}{2}<\frac{y_{2}+y_{3}}{2}<\frac{y_{2}+y_{4}}{2}<\cdots<\frac{y_{995}+y_{997}}{2}<\frac{y_{996}+y_{997}}{2}
$$
there are at least $996+995=1991$ distinct midpoints, and therefore at least 1991 red points. The equality case happens if we take $P_{i}=(0,2 i), i=1,2, \ldots, 997$. The midpoints are $(0, i+j)$, $1 \leq i<j \leq 997$, which are the points $(0, k)$ with $1+2=3 \leq k \leq 996+997=1993$, a total of $1993-3+1=1991$ red points.
|
1991
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Suppose there are 997 points given in a plane. If every two points are joined by a line segment with its midpoint coloured in red, show that there are at least 1991 red points in the plane. Can you find a special case with exactly 1991 red points?
|
Embed the points in the cartesian plane such that no two points have the same $y$-coordinate. Let $P_{1}, P_{2}, \ldots, P_{997}$ be the points and $y_{1}<y_{2}<\ldots<y_{997}$ be their respective $y$-coordinates. Then the $y$-coordinate of the midpoint of $P_{i} P_{i+1}, i=1,2, \ldots, 996$ is $\frac{y_{i}+y_{i+1}}{2}$ and the $y$-coordinate of the midpoint of $P_{i} P_{i+2}, i=1,2, \ldots, 995$ is $\frac{y_{i}+y_{i+2}}{2}$. Since
$$
\frac{y_{1}+y_{2}}{2}<\frac{y_{1}+y_{3}}{2}<\frac{y_{2}+y_{3}}{2}<\frac{y_{2}+y_{4}}{2}<\cdots<\frac{y_{995}+y_{997}}{2}<\frac{y_{996}+y_{997}}{2}
$$
there are at least $996+995=1991$ distinct midpoints, and therefore at least 1991 red points. The equality case happens if we take $P_{i}=(0,2 i), i=1,2, \ldots, 997$. The midpoints are $(0, i+j)$, $1 \leq i<j \leq 997$, which are the points $(0, k)$ with $1+2=3 \leq k \leq 996+997=1993$, a total of $1993-3+1=1991$ red points.
|
{
"resource_path": "APMO/segmented/en-apmo1991_sol.jsonl",
"problem_match": "# Problem 2",
"solution_match": "# Solution\n\n"
}
|
34377d2c-ee80-545c-bcf6-55cfbf014551
| 604,370
|
Let $a_{1}, a_{2}, \ldots, a_{n}, b_{1}, b_{2}, \ldots, b_{n}$ be positive real numbers such that $a_{1}+a_{2}+\cdots+a_{n}=b_{1}+b_{2}+$ $\cdots+b_{n}$. Show that
$$
\frac{a_{1}^{2}}{a_{1}+b_{1}}+\frac{a_{2}^{2}}{a_{2}+b_{2}}+\cdots+\frac{a_{n}^{2}}{a_{n}+b_{n}} \geq \frac{a_{1}+a_{2}+\cdots+a_{n}}{2}
$$
|
By the Cauchy-Schwartz inequality,
$$
\left(\frac{a_{1}^{2}}{a_{1}+b_{1}}+\frac{a_{2}^{2}}{a_{2}+b_{2}}+\cdots+\frac{a_{n}^{2}}{a_{n}+b_{n}}\right)\left(\left(a_{1}+b_{1}\right)+\left(a_{2}+b_{2}\right)+\cdots+\left(a_{n}+b_{n}\right)\right) \geq\left(a_{1}+a_{2}+\cdots+a_{n}\right)^{2} .
$$
Since $\left(\left(a_{1}+b_{1}\right)+\left(a_{2}+b_{2}\right)+\cdots+\left(a_{n}+b_{n}\right)\right)=2\left(a_{1}+a_{2}+\cdots+a_{n}\right)$,
$$
\frac{a_{1}^{2}}{a_{1}+b_{1}}+\frac{a_{2}^{2}}{a_{2}+b_{2}}+\cdots+\frac{a_{n}^{2}}{a_{n}+b_{n}} \geq \frac{\left(a_{1}+a_{2}+\cdots+a_{n}\right)^{2}}{2\left(a_{1}+a_{2}+\cdots+a_{n}\right)}=\frac{a_{1}+a_{2}+\cdots+a_{n}}{2}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a_{1}, a_{2}, \ldots, a_{n}, b_{1}, b_{2}, \ldots, b_{n}$ be positive real numbers such that $a_{1}+a_{2}+\cdots+a_{n}=b_{1}+b_{2}+$ $\cdots+b_{n}$. Show that
$$
\frac{a_{1}^{2}}{a_{1}+b_{1}}+\frac{a_{2}^{2}}{a_{2}+b_{2}}+\cdots+\frac{a_{n}^{2}}{a_{n}+b_{n}} \geq \frac{a_{1}+a_{2}+\cdots+a_{n}}{2}
$$
|
By the Cauchy-Schwartz inequality,
$$
\left(\frac{a_{1}^{2}}{a_{1}+b_{1}}+\frac{a_{2}^{2}}{a_{2}+b_{2}}+\cdots+\frac{a_{n}^{2}}{a_{n}+b_{n}}\right)\left(\left(a_{1}+b_{1}\right)+\left(a_{2}+b_{2}\right)+\cdots+\left(a_{n}+b_{n}\right)\right) \geq\left(a_{1}+a_{2}+\cdots+a_{n}\right)^{2} .
$$
Since $\left(\left(a_{1}+b_{1}\right)+\left(a_{2}+b_{2}\right)+\cdots+\left(a_{n}+b_{n}\right)\right)=2\left(a_{1}+a_{2}+\cdots+a_{n}\right)$,
$$
\frac{a_{1}^{2}}{a_{1}+b_{1}}+\frac{a_{2}^{2}}{a_{2}+b_{2}}+\cdots+\frac{a_{n}^{2}}{a_{n}+b_{n}} \geq \frac{\left(a_{1}+a_{2}+\cdots+a_{n}\right)^{2}}{2\left(a_{1}+a_{2}+\cdots+a_{n}\right)}=\frac{a_{1}+a_{2}+\cdots+a_{n}}{2}
$$
|
{
"resource_path": "APMO/segmented/en-apmo1991_sol.jsonl",
"problem_match": "# Problem 3",
"solution_match": "# Solution\n\n"
}
|
e8fe9e9a-5c87-575d-b5d1-b77329e2e5ae
| 604,382
|
During a break, $n$ children at school sit in a circle around their teacher to play a game. The teacher walks clockwise close to the children and hands out candies to some of them according to the following rule. He selects one child and gives him a candy, then he skips the next child and gives a candy to the next one, then he skips 2 and gives a candy to the next one, then he skips 3, and soon. Determine the values of $n$ for which eventually, perhaps after many rounds, all children will have at least one candy each.
Answer: All powers of 2 .
|
Number the children from 0 to $n-1$. Then the teacher hands candy to children in positions $f(x)=1+2+\cdots+x \bmod n=\frac{x(x+1)}{2} \bmod n$. Our task is to find the range of $f: \mathbb{Z}_{n} \rightarrow \mathbb{Z}_{n}$, and to verify whether the range is $\mathbb{Z}_{n}$, that is, whether $f$ is a bijection.
If $n=2^{a} m, m>1$ odd, look at $f(x)$ modulo $m$. Since $m$ is odd, $m|f(x) \Longleftrightarrow m| x(x+1)$. Then, for instance, $f(x) \equiv 0(\bmod m)$ for $x=0$ and $x=m-1$. This means that $f(x)$ is not a bijection modulo $m$, and there exists $t$ such that $f(x) \not \equiv t(\bmod m)$ for all $x$. By the Chinese Remainder Theorem,
$$
f(x) \equiv t \quad(\bmod n) \Longleftrightarrow \begin{cases}f(x) \equiv t & \left(\bmod 2^{a}\right) \\ f(x) \equiv t & (\bmod m)\end{cases}
$$
Therefore, $f$ is not a bijection modulo $n$.
If $n=2^{a}$, then
$$
f(x)-f(y)=\frac{1}{2}(x(x+1)-y(y+1))=\frac{1}{2}\left(x^{2}-y^{2}+x-y\right)=\frac{(x-y)(x+y+1)}{2} .
$$
and
$$
f(x) \equiv f(y) \quad\left(\bmod 2^{a}\right) \Longleftrightarrow(x-y)(x+y+1) \equiv 0 \quad\left(\bmod 2^{a+1}\right)
$$
If $x$ and $y$ have the same parity, $x+y+1$ is odd and $(*)$ is equivalent to $x \equiv y\left(\bmod 2^{a+1}\right)$. If $x$ and $y$ have different parity,
$$
(*) \Longleftrightarrow x+y+1 \equiv 0 \quad\left(\bmod 2^{a+1}\right)
$$
However, $1 \leq x+y+1 \leq 2\left(2^{a}-1\right)+1=2^{a+1}-1$, so $x+y+1$ is not a multiple of $2^{a+1}$. Therefore $f$ is a bijection if $n$ is a power of 2 .
|
All\ powers\ of\ 2
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
During a break, $n$ children at school sit in a circle around their teacher to play a game. The teacher walks clockwise close to the children and hands out candies to some of them according to the following rule. He selects one child and gives him a candy, then he skips the next child and gives a candy to the next one, then he skips 2 and gives a candy to the next one, then he skips 3, and soon. Determine the values of $n$ for which eventually, perhaps after many rounds, all children will have at least one candy each.
Answer: All powers of 2 .
|
Number the children from 0 to $n-1$. Then the teacher hands candy to children in positions $f(x)=1+2+\cdots+x \bmod n=\frac{x(x+1)}{2} \bmod n$. Our task is to find the range of $f: \mathbb{Z}_{n} \rightarrow \mathbb{Z}_{n}$, and to verify whether the range is $\mathbb{Z}_{n}$, that is, whether $f$ is a bijection.
If $n=2^{a} m, m>1$ odd, look at $f(x)$ modulo $m$. Since $m$ is odd, $m|f(x) \Longleftrightarrow m| x(x+1)$. Then, for instance, $f(x) \equiv 0(\bmod m)$ for $x=0$ and $x=m-1$. This means that $f(x)$ is not a bijection modulo $m$, and there exists $t$ such that $f(x) \not \equiv t(\bmod m)$ for all $x$. By the Chinese Remainder Theorem,
$$
f(x) \equiv t \quad(\bmod n) \Longleftrightarrow \begin{cases}f(x) \equiv t & \left(\bmod 2^{a}\right) \\ f(x) \equiv t & (\bmod m)\end{cases}
$$
Therefore, $f$ is not a bijection modulo $n$.
If $n=2^{a}$, then
$$
f(x)-f(y)=\frac{1}{2}(x(x+1)-y(y+1))=\frac{1}{2}\left(x^{2}-y^{2}+x-y\right)=\frac{(x-y)(x+y+1)}{2} .
$$
and
$$
f(x) \equiv f(y) \quad\left(\bmod 2^{a}\right) \Longleftrightarrow(x-y)(x+y+1) \equiv 0 \quad\left(\bmod 2^{a+1}\right)
$$
If $x$ and $y$ have the same parity, $x+y+1$ is odd and $(*)$ is equivalent to $x \equiv y\left(\bmod 2^{a+1}\right)$. If $x$ and $y$ have different parity,
$$
(*) \Longleftrightarrow x+y+1 \equiv 0 \quad\left(\bmod 2^{a+1}\right)
$$
However, $1 \leq x+y+1 \leq 2\left(2^{a}-1\right)+1=2^{a+1}-1$, so $x+y+1$ is not a multiple of $2^{a+1}$. Therefore $f$ is a bijection if $n$ is a power of 2 .
|
{
"resource_path": "APMO/segmented/en-apmo1991_sol.jsonl",
"problem_match": "# Problem 4",
"solution_match": "# Solution 1"
}
|
a286e0b9-555e-56f0-9690-6a2f0ec7f1fa
| 604,391
|
During a break, $n$ children at school sit in a circle around their teacher to play a game. The teacher walks clockwise close to the children and hands out candies to some of them according to the following rule. He selects one child and gives him a candy, then he skips the next child and gives a candy to the next one, then he skips 2 and gives a candy to the next one, then he skips 3, and soon. Determine the values of $n$ for which eventually, perhaps after many rounds, all children will have at least one candy each.
Answer: All powers of 2 .
|
We give a full description of $a_{n}$, the size of the range of $f$.
Since congruences modulo $n$ are defined, via Chinese Remainder Theorem, by congruences modulo $p^{\alpha}$ for all prime divisors $p$ of $n$ and $\alpha$ being the number of factors $p$ in the factorization of $n, a_{n}=\prod_{p^{\alpha} \| n} a_{p^{\alpha}}$.
Refer to the first solution to check the case $p=2: a_{2^{\alpha}}=2^{\alpha}$.
For an odd prime $p$,
$$
f(x)=\frac{x(x+1)}{2}=\frac{(2 x+1)^{2}-1}{8}
$$
and since $p$ is odd, there is a bijection between the range of $f$ and the quadratic residues modulo $p^{\alpha}$, namely $t \mapsto 8 t+1$. So $a_{p^{\alpha}}$ is the number of quadratic residues modulo $p^{\alpha}$.
Let $g$ be a primitive root of $p^{\alpha}$. Then there are $\frac{1}{2} \phi\left(p^{\alpha}\right)=\frac{p-1}{2} \cdot p^{\alpha-1}$ quadratic residues that are coprime with $p: 1, g^{2}, g^{4}, \ldots, g^{\phi\left(p^{n}\right)-2}$. If $p$ divides a quadratic residue $k p$, that is, $x^{2} \equiv k p$ $\left(\bmod p^{\alpha}\right), \alpha \geq 2$, then $p$ divides $x$ and, therefore, also $k$. Hence $p^{2}$ divides this quadratic residue, and these quadratic residues are $p^{2}$ times each quadratic residue of $p^{\alpha-2}$. Thus
$$
a_{p^{\alpha}}=\frac{p-1}{2} \cdot p^{\alpha-1}+a_{p^{\alpha}-2} .
$$
Since $a_{p}=\frac{p-1}{2}+1$ and $a_{p^{2}}=\frac{p-1}{2} \cdot p+1$, telescoping yields
$$
a_{p^{2 t}}=\frac{p-1}{2}\left(p^{2 t-1}+p^{2 t-3}+\cdots+p\right)+1=\frac{p\left(p^{2 t}-1\right)}{2(p+1)}+1
$$
and
$$
a_{p^{2 t-1}}=\frac{p-1}{2}\left(p^{2 t-2}+p^{2 t-4}+\cdots+1\right)+1=\frac{p^{2 t}-1}{2(p+1)}+1
$$
Now the problem is immediate: if $n$ is divisible by an odd prime $p, a_{p^{\alpha}}<p^{\alpha}$ for all $\alpha$, and since $a_{t} \leq t$ for all $t, a_{n}<n$.
|
All\ powers\ of\ 2
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
During a break, $n$ children at school sit in a circle around their teacher to play a game. The teacher walks clockwise close to the children and hands out candies to some of them according to the following rule. He selects one child and gives him a candy, then he skips the next child and gives a candy to the next one, then he skips 2 and gives a candy to the next one, then he skips 3, and soon. Determine the values of $n$ for which eventually, perhaps after many rounds, all children will have at least one candy each.
Answer: All powers of 2 .
|
We give a full description of $a_{n}$, the size of the range of $f$.
Since congruences modulo $n$ are defined, via Chinese Remainder Theorem, by congruences modulo $p^{\alpha}$ for all prime divisors $p$ of $n$ and $\alpha$ being the number of factors $p$ in the factorization of $n, a_{n}=\prod_{p^{\alpha} \| n} a_{p^{\alpha}}$.
Refer to the first solution to check the case $p=2: a_{2^{\alpha}}=2^{\alpha}$.
For an odd prime $p$,
$$
f(x)=\frac{x(x+1)}{2}=\frac{(2 x+1)^{2}-1}{8}
$$
and since $p$ is odd, there is a bijection between the range of $f$ and the quadratic residues modulo $p^{\alpha}$, namely $t \mapsto 8 t+1$. So $a_{p^{\alpha}}$ is the number of quadratic residues modulo $p^{\alpha}$.
Let $g$ be a primitive root of $p^{\alpha}$. Then there are $\frac{1}{2} \phi\left(p^{\alpha}\right)=\frac{p-1}{2} \cdot p^{\alpha-1}$ quadratic residues that are coprime with $p: 1, g^{2}, g^{4}, \ldots, g^{\phi\left(p^{n}\right)-2}$. If $p$ divides a quadratic residue $k p$, that is, $x^{2} \equiv k p$ $\left(\bmod p^{\alpha}\right), \alpha \geq 2$, then $p$ divides $x$ and, therefore, also $k$. Hence $p^{2}$ divides this quadratic residue, and these quadratic residues are $p^{2}$ times each quadratic residue of $p^{\alpha-2}$. Thus
$$
a_{p^{\alpha}}=\frac{p-1}{2} \cdot p^{\alpha-1}+a_{p^{\alpha}-2} .
$$
Since $a_{p}=\frac{p-1}{2}+1$ and $a_{p^{2}}=\frac{p-1}{2} \cdot p+1$, telescoping yields
$$
a_{p^{2 t}}=\frac{p-1}{2}\left(p^{2 t-1}+p^{2 t-3}+\cdots+p\right)+1=\frac{p\left(p^{2 t}-1\right)}{2(p+1)}+1
$$
and
$$
a_{p^{2 t-1}}=\frac{p-1}{2}\left(p^{2 t-2}+p^{2 t-4}+\cdots+1\right)+1=\frac{p^{2 t}-1}{2(p+1)}+1
$$
Now the problem is immediate: if $n$ is divisible by an odd prime $p, a_{p^{\alpha}}<p^{\alpha}$ for all $\alpha$, and since $a_{t} \leq t$ for all $t, a_{n}<n$.
|
{
"resource_path": "APMO/segmented/en-apmo1991_sol.jsonl",
"problem_match": "# Problem 4",
"solution_match": "# Solution 2"
}
|
a286e0b9-555e-56f0-9690-6a2f0ec7f1fa
| 604,391
|
Given are two tangent circles and a point $P$ on their common tangent perpendicular to the lines joining their centres. Construct with ruler and compass all the circles that are tangent to these two circles and pass through the point $P$.
|
Throughout this problem, we will assume that the given circles are externally tangent, since the problem does not have a solution otherwise.
Let $\Gamma_{1}$ and $\Gamma_{2}$ be the given circles and $T$ be their tangency point. Suppose $\omega$ is a circle that is tangent to $\Gamma_{1}$ and $\Gamma_{2}$ and passes through $P$.
Now invert about point $P$, with radius $P T$. Let any line through $P$ that cuts $\Gamma_{1}$ do so at points $X$ and $Y$. The power of $P$ with respect to $\Gamma_{1}$ is $P T^{2}=P X \cdot P Y$, so $X$ and $Y$ are swapped by this inversion. Therefore $\Gamma_{1}$ is mapped to itself in this inversion. The same applies to $\Gamma_{2}$. Since circle $\omega$ passes through $P$, it is mapped to a line tangent to the images of $\Gamma_{1}$ (itself) and $\Gamma_{2}$ (also itself), that is, a common tangent line. This common tangent cannot be $P T$, as $P T$ is also mapped to itself. Since $\Gamma_{1}$ and $\Gamma_{2}$ have exactly other two common tangent lines, there are two solutions: the inverses of the tangent lines.
We proceed with the construction with the aid of some macro constructions that will be detailed later.
Step 1. Draw the common tangents to $\Gamma_{1}$ and $\Gamma_{2}$.
Step 2. For each common tangent $t$, draw the projection $P_{t}$ of $P$ onto $t$.
Step 3. Find the inverse $P_{1}$ of $P_{t}$ with respect to the circle with center $P$ and radius $P T$.
Step 4. $\omega_{t}$ is the circle with diameter $P P_{1}$.
Let's work out the details for steps 1 and 3 . Steps 2 and 4 are immediate.
Step 1. In this particular case in which $\Gamma_{1}$ and $\Gamma_{2}$ are externally tangent, there is a small shortcut:
- Draw the circle with diameter on the two centers $O_{1}$ of $\Gamma_{1}$ and $O_{2}$ of $\Gamma_{2}$, and find its center $O$.
- Let this circle meet common tangent line $O P$ at points $Q, R$. The required lines are the perpendicular to $O Q$ at $Q$ and the perpendicular to $O R$ at $R$.
Let's show why this construction works. Let $R_{i}$ be the radius of circle $\Gamma_{i}$ and suppose without loss of generality that $R_{1} \leq R_{2}$. Note that $O Q=\frac{1}{2} O_{1} O_{2}=\frac{R_{1}+R_{2}}{2}, O T=O O_{1}-R_{1}=\frac{R_{2}-R_{1}}{2}$, so
$$
\sin \angle T Q O=\frac{O T}{O Q}=\frac{R_{2}-R_{1}}{R_{1}+R_{2}}
$$
which is also the sine of the angle between $O_{1} O_{2}$ and the common tangent lines.
Let $t$ be the perpendicular to $O Q$ through $Q$. Then $\angle\left(t, O_{1} O_{2}\right)=\angle(O Q, Q T)=\angle T Q O$, and $t$ is parallel to a common tangent line. Since
$$
d(O, t)=O Q=\frac{R_{1}+R_{2}}{2}=\frac{d\left(O_{1}, t\right)+d\left(O_{2}, t\right)}{2}
$$
and $O$ is the midpoint of $O_{1} O_{2}, O$ is also at the same distance from $t$ and the common tangent line, so these two lines coincide.
Step 3. Finding the inverse of a point $X$ given the inversion circle $\Omega$ with center $O$ is a well known procedure, but we describe it here for the sake of completeness.
- If $X$ lies in $\Omega$, then its inverse is $X$.
- If $X$ lies in the interior of $\Omega$, draw ray $O X$, then the perpendicular line $\ell$ to $O X$ at $X$. Let $\ell$ meet $\Omega$ at a point $Y$. The inverse of $X$ is the intersection $X^{\prime}$ of $O X$ and the line perpendicular to $O Y$ at $Y$. This is because $O Y X^{\prime}$ is a right triangle with altitude $Y X$, and therefore $O X \cdot O X^{\prime}=O Y^{2}$.
- If $X$ is in the exterior of $\Omega$, draw ray $O X$ and one of the tangent lines $\ell$ from $X$ to $\Omega$ (just connect $X$ to one of the intersections of $\Omega$ and the circle with diameter $O X$ ). Let $\ell$ touch $\Omega$ at a point $Y$. The inverse of $X$ is the projection $X^{\prime}$ of $Y$ onto $O X$. This is because $O Y X^{\prime}$ is a right triangle with altitude $Y X^{\prime}$, and therefore $O X \cdot O X^{\prime}=O Y^{2}$.
$X$ is inside $\Omega$
|
not found
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Given are two tangent circles and a point $P$ on their common tangent perpendicular to the lines joining their centres. Construct with ruler and compass all the circles that are tangent to these two circles and pass through the point $P$.
|
Throughout this problem, we will assume that the given circles are externally tangent, since the problem does not have a solution otherwise.
Let $\Gamma_{1}$ and $\Gamma_{2}$ be the given circles and $T$ be their tangency point. Suppose $\omega$ is a circle that is tangent to $\Gamma_{1}$ and $\Gamma_{2}$ and passes through $P$.
Now invert about point $P$, with radius $P T$. Let any line through $P$ that cuts $\Gamma_{1}$ do so at points $X$ and $Y$. The power of $P$ with respect to $\Gamma_{1}$ is $P T^{2}=P X \cdot P Y$, so $X$ and $Y$ are swapped by this inversion. Therefore $\Gamma_{1}$ is mapped to itself in this inversion. The same applies to $\Gamma_{2}$. Since circle $\omega$ passes through $P$, it is mapped to a line tangent to the images of $\Gamma_{1}$ (itself) and $\Gamma_{2}$ (also itself), that is, a common tangent line. This common tangent cannot be $P T$, as $P T$ is also mapped to itself. Since $\Gamma_{1}$ and $\Gamma_{2}$ have exactly other two common tangent lines, there are two solutions: the inverses of the tangent lines.

We proceed with the construction with the aid of some macro constructions that will be detailed later.
Step 1. Draw the common tangents to $\Gamma_{1}$ and $\Gamma_{2}$.
Step 2. For each common tangent $t$, draw the projection $P_{t}$ of $P$ onto $t$.
Step 3. Find the inverse $P_{1}$ of $P_{t}$ with respect to the circle with center $P$ and radius $P T$.
Step 4. $\omega_{t}$ is the circle with diameter $P P_{1}$.
Let's work out the details for steps 1 and 3 . Steps 2 and 4 are immediate.
Step 1. In this particular case in which $\Gamma_{1}$ and $\Gamma_{2}$ are externally tangent, there is a small shortcut:
- Draw the circle with diameter on the two centers $O_{1}$ of $\Gamma_{1}$ and $O_{2}$ of $\Gamma_{2}$, and find its center $O$.
- Let this circle meet common tangent line $O P$ at points $Q, R$. The required lines are the perpendicular to $O Q$ at $Q$ and the perpendicular to $O R$ at $R$.

Let's show why this construction works. Let $R_{i}$ be the radius of circle $\Gamma_{i}$ and suppose without loss of generality that $R_{1} \leq R_{2}$. Note that $O Q=\frac{1}{2} O_{1} O_{2}=\frac{R_{1}+R_{2}}{2}, O T=O O_{1}-R_{1}=\frac{R_{2}-R_{1}}{2}$, so
$$
\sin \angle T Q O=\frac{O T}{O Q}=\frac{R_{2}-R_{1}}{R_{1}+R_{2}}
$$
which is also the sine of the angle between $O_{1} O_{2}$ and the common tangent lines.
Let $t$ be the perpendicular to $O Q$ through $Q$. Then $\angle\left(t, O_{1} O_{2}\right)=\angle(O Q, Q T)=\angle T Q O$, and $t$ is parallel to a common tangent line. Since
$$
d(O, t)=O Q=\frac{R_{1}+R_{2}}{2}=\frac{d\left(O_{1}, t\right)+d\left(O_{2}, t\right)}{2}
$$
and $O$ is the midpoint of $O_{1} O_{2}, O$ is also at the same distance from $t$ and the common tangent line, so these two lines coincide.
Step 3. Finding the inverse of a point $X$ given the inversion circle $\Omega$ with center $O$ is a well known procedure, but we describe it here for the sake of completeness.
- If $X$ lies in $\Omega$, then its inverse is $X$.
- If $X$ lies in the interior of $\Omega$, draw ray $O X$, then the perpendicular line $\ell$ to $O X$ at $X$. Let $\ell$ meet $\Omega$ at a point $Y$. The inverse of $X$ is the intersection $X^{\prime}$ of $O X$ and the line perpendicular to $O Y$ at $Y$. This is because $O Y X^{\prime}$ is a right triangle with altitude $Y X$, and therefore $O X \cdot O X^{\prime}=O Y^{2}$.
- If $X$ is in the exterior of $\Omega$, draw ray $O X$ and one of the tangent lines $\ell$ from $X$ to $\Omega$ (just connect $X$ to one of the intersections of $\Omega$ and the circle with diameter $O X$ ). Let $\ell$ touch $\Omega$ at a point $Y$. The inverse of $X$ is the projection $X^{\prime}$ of $Y$ onto $O X$. This is because $O Y X^{\prime}$ is a right triangle with altitude $Y X^{\prime}$, and therefore $O X \cdot O X^{\prime}=O Y^{2}$.

$X$ is inside $\Omega$

|
{
"resource_path": "APMO/segmented/en-apmo1991_sol.jsonl",
"problem_match": "# Problem 5",
"solution_match": "# Solution\n\n"
}
|
e08fa1d8-2748-596d-8b32-52ceb4733c10
| 604,414
|
A triangle with sides $a, b$, and $c$ is given. Denote by $s$ the semiperimeter, that is $s=(a+b+c) / 2$. Construct a triangle with sides $s-a, s-b$, and $s-c$. This process is repeated until a triangle can no longer be constructed with the sidelengths given.
For which original triangles can this process be repeated indefinitely?
Answer: Only equilateral triangles.
|
The perimeter of each new triangle constructed by the process is $(s-a)+(s-b)+(s-c)=$ $3 s-(a+b+c)=3 s-2 s=s$, that is, it is halved. Consider a new equivalent process in which a similar triangle with sidelengths $2(s-a), 2(s-b), 2(s-c)$ is constructed, so the perimeter is kept invariant.
Suppose without loss of generality that $a \leq b \leq c$. Then $2(s-c) \leq 2(s-b) \leq 2(s-a)$, and the difference between the largest side and the smallest side changes from $c-a$ to $2(s-a)-2(s-c)=$ $2(c-a)$, that is, it doubles. Therefore, if $c-a>0$ then eventually this difference becomes larger than $a+b+c$, and it's immediate that a triangle cannot be constructed with the sidelengths. Hence the only possibility is $c-a=0 \Longrightarrow a=b=c$, and it is clear that equilateral triangles can yield an infinite process, because all generated triangles are equilateral.
|
a=b=c
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A triangle with sides $a, b$, and $c$ is given. Denote by $s$ the semiperimeter, that is $s=(a+b+c) / 2$. Construct a triangle with sides $s-a, s-b$, and $s-c$. This process is repeated until a triangle can no longer be constructed with the sidelengths given.
For which original triangles can this process be repeated indefinitely?
Answer: Only equilateral triangles.
|
The perimeter of each new triangle constructed by the process is $(s-a)+(s-b)+(s-c)=$ $3 s-(a+b+c)=3 s-2 s=s$, that is, it is halved. Consider a new equivalent process in which a similar triangle with sidelengths $2(s-a), 2(s-b), 2(s-c)$ is constructed, so the perimeter is kept invariant.
Suppose without loss of generality that $a \leq b \leq c$. Then $2(s-c) \leq 2(s-b) \leq 2(s-a)$, and the difference between the largest side and the smallest side changes from $c-a$ to $2(s-a)-2(s-c)=$ $2(c-a)$, that is, it doubles. Therefore, if $c-a>0$ then eventually this difference becomes larger than $a+b+c$, and it's immediate that a triangle cannot be constructed with the sidelengths. Hence the only possibility is $c-a=0 \Longrightarrow a=b=c$, and it is clear that equilateral triangles can yield an infinite process, because all generated triangles are equilateral.
|
{
"resource_path": "APMO/segmented/en-apmo1992_sol.jsonl",
"problem_match": "# Problem 1",
"solution_match": "# Solution\n\n"
}
|
ef5f9a15-b67b-5b8e-aed5-0dfe296290a9
| 604,428
|
In a circle $C$ with centre $O$ and radius $r$, let $C_{1}, C_{2}$ be two circles with centres $O_{1}, O_{2}$ and radii $r_{1}, r_{2}$ respectively, so that each circle $C_{i}$ is internally tangent to $C$ at $A_{i}$ and so that $C_{1}, C_{2}$ are externally tangent to each other at $A$.
Prove that the three lines $O A, O_{1} A_{2}$, and $O_{2} A_{1}$ are concurrent.
|
Because of the tangencies, the following triples of points (two centers and a tangency point) are collinear:
$$
O_{1} ; O_{2} ; A, \quad O ; O_{1} ; A_{1}, \quad O ; O_{2} ; A_{2}
$$
Because of that we can ignore the circles and only draw their centers and tangency points.
Now the problem is immediate from Ceva's theorem in triangle $O O_{1} O_{2}$, because
$$
\frac{O A_{1}}{A_{1} O_{1}} \cdot \frac{O_{1} A}{A O_{2}} \cdot \frac{O_{2} A_{2}}{A_{2} O}=\frac{r}{r_{1}} \cdot \frac{r_{1}}{r_{2}} \cdot \frac{r_{2}}{r}=1
$$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In a circle $C$ with centre $O$ and radius $r$, let $C_{1}, C_{2}$ be two circles with centres $O_{1}, O_{2}$ and radii $r_{1}, r_{2}$ respectively, so that each circle $C_{i}$ is internally tangent to $C$ at $A_{i}$ and so that $C_{1}, C_{2}$ are externally tangent to each other at $A$.
Prove that the three lines $O A, O_{1} A_{2}$, and $O_{2} A_{1}$ are concurrent.
|
Because of the tangencies, the following triples of points (two centers and a tangency point) are collinear:
$$
O_{1} ; O_{2} ; A, \quad O ; O_{1} ; A_{1}, \quad O ; O_{2} ; A_{2}
$$
Because of that we can ignore the circles and only draw their centers and tangency points.

Now the problem is immediate from Ceva's theorem in triangle $O O_{1} O_{2}$, because
$$
\frac{O A_{1}}{A_{1} O_{1}} \cdot \frac{O_{1} A}{A O_{2}} \cdot \frac{O_{2} A_{2}}{A_{2} O}=\frac{r}{r_{1}} \cdot \frac{r_{1}}{r_{2}} \cdot \frac{r_{2}}{r}=1
$$
|
{
"resource_path": "APMO/segmented/en-apmo1992_sol.jsonl",
"problem_match": "# Problem 2",
"solution_match": "# Solution\n\n"
}
|
ffb81a07-18b5-55d8-b41e-205d7c2461c9
| 604,440
|
Let $n$ be an integer such that $n>3$. Suppose that we choose three numbers from the set $\{1,2, \ldots, n\}$. Using each of these three numbers only once and using addition, multiplication, and parenthesis, let us form all possible combinations.
(a) Show that if we choose all three numbers greater than $n / 2$, then the values of these combinations are all distinct.
(b) Let $p$ be a prime number such that $p \leq \sqrt{n}$. Show that the number of ways of choosing three numbers so that the smallest one is $p$ and the values of the combinations are not all distinct is precisely the number of positive divisors of $p-1$.
|
In both items, the smallest chosen number is at least 2: in part (a), $n / 2>1$ and in part (b), $p$ is a prime. So let $1<x<y<z$ be the chosen numbers. Then all possible combinations are
$$
x+y+z, \quad x+y z, \quad x y+z, \quad y+z x, \quad(x+y) z, \quad(z+x) y, \quad(x+y) z, \quad x y z
$$
Since, for $1<m<n$ and $t>1,(m-1)(n-1) \geq 1 \cdot 2 \Longrightarrow m n>m+n, t n+m-(t m+n)=$ $(t-1)(n-m)>0 \Longrightarrow t n+m>t m+n$, and $(t+m) n-(t+n) m=t(n-m)>0$,
$$
x+y+z<z+x y<y+z x<x+y z
$$
and
$$
(y+z) x<(x+z) y<(x+y) z<x y z .
$$
Also, $(y+z) x-(y+z x)=(x-1) y>0 \Longrightarrow(y+z) x>y+z x$ and $(x+z) y-(x+y z)=$ $(y-1) x>0 \Longrightarrow(x+z) y>x+y z$. Therefore the only numbers that can be equal are $x+y z$ and $(y+z) x$. In this case,
$$
x+y z=(y+z) x \Longleftrightarrow(y-x)(z-x)=x(x-1)
$$
Now we can solve the items.
(a) if $n / 2<x<y<z$ then $z-x<n / 2$, and since $y-x<z-x, y-x<n / 2-1$; then
$$
(y-x)(z-x)<\frac{n}{2}\left(\frac{n}{2}-1\right)<x(x-1)
$$
and therefore $x+y z<(y+z) x$.
(b) if $x=p$, then $(y-p)(z-p)=p(p-1)$. Since $y-p<z-p,(y-p)^{2}<(y-p)(z-p)=$ $p(p-1) \Longrightarrow y-p<p$, that is, $p$ does not divide $y-p$. Then $y-p$ is a divisor $d$ of $p-1$ and $z-p=\frac{p(p-1)}{d}$. Therefore,
$$
x=p, \quad, y=p+d, \quad z=p+\frac{p(p-1)}{d}
$$
which is a solution for every divisor $d$ of $p-1$ because
$$
x=p<y=p+d<2 p \leq p+p \cdot \frac{p-1}{d}=z .
$$
Comment: If $x=1$ was allowed, then any choice $1, y, z$ would have repeated numbers in the combination, as $1 \cdot y+z=y+1 \cdot z$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n$ be an integer such that $n>3$. Suppose that we choose three numbers from the set $\{1,2, \ldots, n\}$. Using each of these three numbers only once and using addition, multiplication, and parenthesis, let us form all possible combinations.
(a) Show that if we choose all three numbers greater than $n / 2$, then the values of these combinations are all distinct.
(b) Let $p$ be a prime number such that $p \leq \sqrt{n}$. Show that the number of ways of choosing three numbers so that the smallest one is $p$ and the values of the combinations are not all distinct is precisely the number of positive divisors of $p-1$.
|
In both items, the smallest chosen number is at least 2: in part (a), $n / 2>1$ and in part (b), $p$ is a prime. So let $1<x<y<z$ be the chosen numbers. Then all possible combinations are
$$
x+y+z, \quad x+y z, \quad x y+z, \quad y+z x, \quad(x+y) z, \quad(z+x) y, \quad(x+y) z, \quad x y z
$$
Since, for $1<m<n$ and $t>1,(m-1)(n-1) \geq 1 \cdot 2 \Longrightarrow m n>m+n, t n+m-(t m+n)=$ $(t-1)(n-m)>0 \Longrightarrow t n+m>t m+n$, and $(t+m) n-(t+n) m=t(n-m)>0$,
$$
x+y+z<z+x y<y+z x<x+y z
$$
and
$$
(y+z) x<(x+z) y<(x+y) z<x y z .
$$
Also, $(y+z) x-(y+z x)=(x-1) y>0 \Longrightarrow(y+z) x>y+z x$ and $(x+z) y-(x+y z)=$ $(y-1) x>0 \Longrightarrow(x+z) y>x+y z$. Therefore the only numbers that can be equal are $x+y z$ and $(y+z) x$. In this case,
$$
x+y z=(y+z) x \Longleftrightarrow(y-x)(z-x)=x(x-1)
$$
Now we can solve the items.
(a) if $n / 2<x<y<z$ then $z-x<n / 2$, and since $y-x<z-x, y-x<n / 2-1$; then
$$
(y-x)(z-x)<\frac{n}{2}\left(\frac{n}{2}-1\right)<x(x-1)
$$
and therefore $x+y z<(y+z) x$.
(b) if $x=p$, then $(y-p)(z-p)=p(p-1)$. Since $y-p<z-p,(y-p)^{2}<(y-p)(z-p)=$ $p(p-1) \Longrightarrow y-p<p$, that is, $p$ does not divide $y-p$. Then $y-p$ is a divisor $d$ of $p-1$ and $z-p=\frac{p(p-1)}{d}$. Therefore,
$$
x=p, \quad, y=p+d, \quad z=p+\frac{p(p-1)}{d}
$$
which is a solution for every divisor $d$ of $p-1$ because
$$
x=p<y=p+d<2 p \leq p+p \cdot \frac{p-1}{d}=z .
$$
Comment: If $x=1$ was allowed, then any choice $1, y, z$ would have repeated numbers in the combination, as $1 \cdot y+z=y+1 \cdot z$.
|
{
"resource_path": "APMO/segmented/en-apmo1992_sol.jsonl",
"problem_match": "# Problem 3",
"solution_match": "# Solution\n\n"
}
|
b52e4aa1-0199-5e11-88b8-bb3a94eec199
| 604,457
|
Determine all pairs $(h, s)$ of positive integers with the following property: If one draws $h$ horizontal lines and another $s$ lines which satisfy
(i) they are not horizontal,
(ii) no two of them are parallel,
(iii) no three of the $h+s$ lines are concurrent,
then the number of regions formed by these $h+s$ lines is 1992 .
Answer: $(995,1),(176,10)$, and $(80,21)$.
|
Let $a_{h, s}$ the number of regions formed by $h$ horizontal lines and $s$ another lines as described in the problem. Let $\mathcal{F}_{h, s}$ be the union of the $h+s$ lines and pick any line $\ell$. If it intersects the other lines in $n$ (distinct!) points then $\ell$ is partitioned into $n-1$ line segments and 2 rays, which delimit regions. Therefore if we remove $\ell$ the number of regions decreases by exactly $n-1+2=n+1$.
Then $a_{0,0}=1$ (no lines means there is only one region), and since every one of $s$ lines intersects the other $s-1$ lines, $a_{0, s}=a_{0, s-1}+s$ for $s \geq 0$. Summing yields
$$
a_{0, s}=s+(s-1)+\cdots+1+a_{0,0}=\frac{s^{2}+s+2}{2} .
$$
Each horizontal line only intersects the $s$ non-horizontal lines, so $a_{h, s}=a_{h-1, s}+s+1$, which implies
$$
a_{h, s}=a_{0, s}+h(s+1)=\frac{s^{2}+s+2}{2}+h(s+1) .
$$
Our final task is solving
$$
a_{h, s}=1992 \Longleftrightarrow \frac{s^{2}+s+2}{2}+h(s+1)=1992 \Longleftrightarrow(s+1)(s+2 h)=2 \cdot 1991=2 \cdot 11 \cdot 181
$$
The divisors of $2 \cdot 1991$ are $1,2,11,22,181,362,1991,3982$. Since $s, h>0,2 \leq s+1<s+2 h$, so the possibilities for $s+1$ can only be 2,11 and 22 , yielding the following possibilities for $(h, s)$ :
$$
(995,1), \quad(176,10), \quad \text { and }(80,21) .
$$
|
(995,1), (176,10), (80,21)
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Determine all pairs $(h, s)$ of positive integers with the following property: If one draws $h$ horizontal lines and another $s$ lines which satisfy
(i) they are not horizontal,
(ii) no two of them are parallel,
(iii) no three of the $h+s$ lines are concurrent,
then the number of regions formed by these $h+s$ lines is 1992 .
Answer: $(995,1),(176,10)$, and $(80,21)$.
|
Let $a_{h, s}$ the number of regions formed by $h$ horizontal lines and $s$ another lines as described in the problem. Let $\mathcal{F}_{h, s}$ be the union of the $h+s$ lines and pick any line $\ell$. If it intersects the other lines in $n$ (distinct!) points then $\ell$ is partitioned into $n-1$ line segments and 2 rays, which delimit regions. Therefore if we remove $\ell$ the number of regions decreases by exactly $n-1+2=n+1$.
Then $a_{0,0}=1$ (no lines means there is only one region), and since every one of $s$ lines intersects the other $s-1$ lines, $a_{0, s}=a_{0, s-1}+s$ for $s \geq 0$. Summing yields
$$
a_{0, s}=s+(s-1)+\cdots+1+a_{0,0}=\frac{s^{2}+s+2}{2} .
$$
Each horizontal line only intersects the $s$ non-horizontal lines, so $a_{h, s}=a_{h-1, s}+s+1$, which implies
$$
a_{h, s}=a_{0, s}+h(s+1)=\frac{s^{2}+s+2}{2}+h(s+1) .
$$
Our final task is solving
$$
a_{h, s}=1992 \Longleftrightarrow \frac{s^{2}+s+2}{2}+h(s+1)=1992 \Longleftrightarrow(s+1)(s+2 h)=2 \cdot 1991=2 \cdot 11 \cdot 181
$$
The divisors of $2 \cdot 1991$ are $1,2,11,22,181,362,1991,3982$. Since $s, h>0,2 \leq s+1<s+2 h$, so the possibilities for $s+1$ can only be 2,11 and 22 , yielding the following possibilities for $(h, s)$ :
$$
(995,1), \quad(176,10), \quad \text { and }(80,21) .
$$
|
{
"resource_path": "APMO/segmented/en-apmo1992_sol.jsonl",
"problem_match": "# Problem 4",
"solution_match": "# Solution\n\n"
}
|
ae9a860d-e440-5433-b4ef-89a69c0b2eef
| 604,469
|
Find a sequence of maximal length consisting of non-zero integers in which the sum of any seven consecutive terms is positive and that of any eleven consecutive terms is negative.
Answer: The maximum length is 16 . There are several possible sequences with this length; one such sequence is $(-7,-7,18,-7,-7,-7,18,-7,-7,18,-7,-7,-7,18,-7,-7)$.
|
Suppose it is possible to have more than 16 terms in the sequence. Let $a_{1}, a_{2}, \ldots, a_{17}$ be the first 17 terms of the sequence. Consider the following array of terms in the sequence:
| $a_{1}$ | $a_{2}$ | $a_{3}$ | $a_{4}$ | $a_{5}$ | $a_{6}$ | $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $a_{2}$ | $a_{3}$ | $a_{4}$ | $a_{5}$ | $a_{6}$ | $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ | $a_{12}$ |
| $a_{3}$ | $a_{4}$ | $a_{5}$ | $a_{6}$ | $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ | $a_{12}$ | $a_{13}$ |
| $a_{4}$ | $a_{5}$ | $a_{6}$ | $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ | $a_{12}$ | $a_{13}$ | $a_{14}$ |
| $a_{5}$ | $a_{6}$ | $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ | $a_{12}$ | $a_{13}$ | $a_{14}$ | $a_{15}$ |
| $a_{6}$ | $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ | $a_{12}$ | $a_{13}$ | $a_{14}$ | $a_{15}$ | $a_{16}$ |
| $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ | $a_{12}$ | $a_{13}$ | $a_{14}$ | $a_{15}$ | $a_{16}$ | $a_{17}$ |
Let $S$ the sum of the numbers in the array. If we sum by rows we obtain negative sums in each row, so $S<0$; however, it we sum by columns we obtain positive sums in each column, so $S>0$, a contradiction. This implies that the sequence cannot have more than 16 terms. One idea to find a suitable sequence with 16 terms is considering cycles of 7 numbers. For instance, one can try
$$
-a,-a, b,-a,-a,-a, b,-a,-a, b,-a,-a,-a, b,-a,-a .
$$
The sum of every seven consecutive numbers is $-5 a+2 b$ and the sum of every eleven consecutive numbers is $-8 a+3 b$, so $-5 a+2 b>0$ and $-8 a+3 b<0$, that is,
$$
\frac{5 a}{2}<b<\frac{8 a}{3} \Longleftrightarrow 15 a<6 b<16 a
$$
Then we can choose, say, $a=7$ and $105<6 b<112 \Longleftrightarrow b=18$. A valid sequence is then
$$
-7,-7,18,-7,-7,-7,18,-7,-7,18,-7,-7,-7,18,-7,-7
$$
|
-7,-7,18,-7,-7,-7,18,-7,-7,18,-7,-7,-7,18,-7,-7
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Find a sequence of maximal length consisting of non-zero integers in which the sum of any seven consecutive terms is positive and that of any eleven consecutive terms is negative.
Answer: The maximum length is 16 . There are several possible sequences with this length; one such sequence is $(-7,-7,18,-7,-7,-7,18,-7,-7,18,-7,-7,-7,18,-7,-7)$.
|
Suppose it is possible to have more than 16 terms in the sequence. Let $a_{1}, a_{2}, \ldots, a_{17}$ be the first 17 terms of the sequence. Consider the following array of terms in the sequence:
| $a_{1}$ | $a_{2}$ | $a_{3}$ | $a_{4}$ | $a_{5}$ | $a_{6}$ | $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $a_{2}$ | $a_{3}$ | $a_{4}$ | $a_{5}$ | $a_{6}$ | $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ | $a_{12}$ |
| $a_{3}$ | $a_{4}$ | $a_{5}$ | $a_{6}$ | $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ | $a_{12}$ | $a_{13}$ |
| $a_{4}$ | $a_{5}$ | $a_{6}$ | $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ | $a_{12}$ | $a_{13}$ | $a_{14}$ |
| $a_{5}$ | $a_{6}$ | $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ | $a_{12}$ | $a_{13}$ | $a_{14}$ | $a_{15}$ |
| $a_{6}$ | $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ | $a_{12}$ | $a_{13}$ | $a_{14}$ | $a_{15}$ | $a_{16}$ |
| $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ | $a_{12}$ | $a_{13}$ | $a_{14}$ | $a_{15}$ | $a_{16}$ | $a_{17}$ |
Let $S$ the sum of the numbers in the array. If we sum by rows we obtain negative sums in each row, so $S<0$; however, it we sum by columns we obtain positive sums in each column, so $S>0$, a contradiction. This implies that the sequence cannot have more than 16 terms. One idea to find a suitable sequence with 16 terms is considering cycles of 7 numbers. For instance, one can try
$$
-a,-a, b,-a,-a,-a, b,-a,-a, b,-a,-a,-a, b,-a,-a .
$$
The sum of every seven consecutive numbers is $-5 a+2 b$ and the sum of every eleven consecutive numbers is $-8 a+3 b$, so $-5 a+2 b>0$ and $-8 a+3 b<0$, that is,
$$
\frac{5 a}{2}<b<\frac{8 a}{3} \Longleftrightarrow 15 a<6 b<16 a
$$
Then we can choose, say, $a=7$ and $105<6 b<112 \Longleftrightarrow b=18$. A valid sequence is then
$$
-7,-7,18,-7,-7,-7,18,-7,-7,18,-7,-7,-7,18,-7,-7
$$
|
{
"resource_path": "APMO/segmented/en-apmo1992_sol.jsonl",
"problem_match": "# Problem 5",
"solution_match": "# Solution\n\n"
}
|
afbefb89-afc4-50d1-ab7a-33f76685ff2e
| 604,481
|
Let $A B C D$ be a quadrilateral such that all sides have equal length and angle $\angle A B C$ is 60 degrees. Let $\ell$ be a line passing through $D$ and not intersecting the quadrilateral (except at $D)$. Let $E$ and $F$ be the points of intersection of $\ell$ with $A B$ and $B C$ respectively. Let $M$ be the point of intersection of $C E$ and $A F$.
Prove that $C A^{2}=C M \times C E$.
|
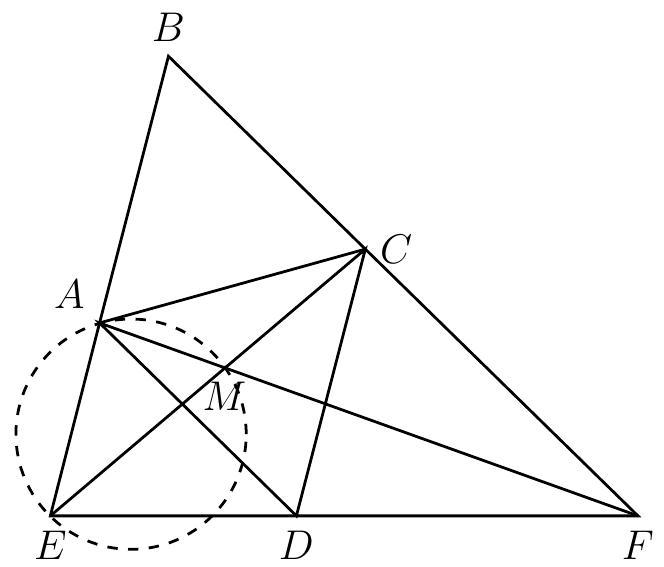
Triangles $A E D$ and $C D F$ are similar, because $A D \| C F$ and $A E \| C D$. Thus, since $A B C$ and $A C D$ are equilateral triangles,
$$
\frac{A E}{C D}=\frac{A D}{C F} \Longleftrightarrow \frac{A E}{A C}=\frac{A C}{C F}
$$
The last equality combined with
$$
\angle E A C=180^{\circ}-\angle B A C=120^{\circ}=\angle A C F
$$
shows that triangles $E A C$ and $A C F$ are also similar. Therefore $\angle C A M=\angle C A F=\angle A E C$, which implies that line $A C$ is tangent to the circumcircle of $A M E$. By the power of a point, $C A^{2}=C M \cdot C E$, and we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a quadrilateral such that all sides have equal length and angle $\angle A B C$ is 60 degrees. Let $\ell$ be a line passing through $D$ and not intersecting the quadrilateral (except at $D)$. Let $E$ and $F$ be the points of intersection of $\ell$ with $A B$ and $B C$ respectively. Let $M$ be the point of intersection of $C E$ and $A F$.
Prove that $C A^{2}=C M \times C E$.
|

Triangles $A E D$ and $C D F$ are similar, because $A D \| C F$ and $A E \| C D$. Thus, since $A B C$ and $A C D$ are equilateral triangles,
$$
\frac{A E}{C D}=\frac{A D}{C F} \Longleftrightarrow \frac{A E}{A C}=\frac{A C}{C F}
$$
The last equality combined with
$$
\angle E A C=180^{\circ}-\angle B A C=120^{\circ}=\angle A C F
$$
shows that triangles $E A C$ and $A C F$ are also similar. Therefore $\angle C A M=\angle C A F=\angle A E C$, which implies that line $A C$ is tangent to the circumcircle of $A M E$. By the power of a point, $C A^{2}=C M \cdot C E$, and we are done.
|
{
"resource_path": "APMO/segmented/en-apmo1993_sol.jsonl",
"problem_match": "# Problem 1",
"solution_match": "# Solution\n\n"
}
|
93fdf523-4aa5-5c8a-9d13-256f9c9907cd
| 604,496
|
Find the total number of different integer values the function
$$
f(x)=[x]+[2 x]+\left[\frac{5 x}{3}\right]+[3 x]+[4 x]
$$
takes for real numbers $x$ with $0 \leq x \leq 100$.
Note: $[t]$ is the largest integer that does not exceed $t$.
Answer: 734.
|
Note that, since $[x+n]=[x]+n$ for any integer $n$,
$$
f(x+3)=[x+3]+[2(x+3)]+\left[\frac{5(x+3)}{3}\right]+[3(x+3)]+[4(x+3)]=f(x)+35,
$$
one only needs to investigate the interval $[0,3)$.
The numbers in this interval at which at least one of the real numbers $x, 2 x, \frac{5 x}{3}, 3 x, 4 x$ is an integer are
- $0,1,2$ for $x$;
- $\frac{n}{2}, 0 \leq n \leq 5$ for $2 x$;
- $\frac{3 n}{5}, 0 \leq n \leq 4$ for $\frac{5 x}{3}$;
- $\frac{n}{3}, 0 \leq n \leq 8$ for $3 x$;
- $\frac{n}{4}, 0 \leq n \leq 11$ for $4 x$.
Of these numbers there are
- 3 integers $(0,1,2)$;
- 3 irreducible fractions with 2 as denominator (the numerators are $1,3,5$ );
- 6 irreducible fractions with 3 as denominator (the numerators are $1,2,4,5,7,8$ );
- 6 irreducible fractions with 4 as denominator (the numerators are $1,3,5,7,9,11,13,15$ );
- 4 irreducible fractions with 5 as denominator (the numerators are 3,6,9,12).
Therefore $f(x)$ increases 22 times per interval. Since $100=33 \cdot 3+1$, there are $33 \cdot 22$ changes of value in $[0,99)$. Finally, there are 8 more changes in [99,100]: 99, 100, $99 \frac{1}{2}, 99 \frac{1}{3}, 99 \frac{2}{3}, 99 \frac{1}{4}$, $99 \frac{3}{4}, 99 \frac{3}{5}$.
The total is then $33 \cdot 22+8=734$.
Comment: A more careful inspection shows that the range of $f$ are the numbers congruent modulo 35 to one of
$$
0,1,2,4,5,6,7,11,12,13,14,16,17,18,19,23,24,25,26,28,29,30
$$
in the interval $[0, f(100)]=[0,1166]$. Since $1166 \equiv 11(\bmod 35)$, this comprises 33 cycles plus the 8 numbers in the previous list.
|
734
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the total number of different integer values the function
$$
f(x)=[x]+[2 x]+\left[\frac{5 x}{3}\right]+[3 x]+[4 x]
$$
takes for real numbers $x$ with $0 \leq x \leq 100$.
Note: $[t]$ is the largest integer that does not exceed $t$.
Answer: 734.
|
Note that, since $[x+n]=[x]+n$ for any integer $n$,
$$
f(x+3)=[x+3]+[2(x+3)]+\left[\frac{5(x+3)}{3}\right]+[3(x+3)]+[4(x+3)]=f(x)+35,
$$
one only needs to investigate the interval $[0,3)$.
The numbers in this interval at which at least one of the real numbers $x, 2 x, \frac{5 x}{3}, 3 x, 4 x$ is an integer are
- $0,1,2$ for $x$;
- $\frac{n}{2}, 0 \leq n \leq 5$ for $2 x$;
- $\frac{3 n}{5}, 0 \leq n \leq 4$ for $\frac{5 x}{3}$;
- $\frac{n}{3}, 0 \leq n \leq 8$ for $3 x$;
- $\frac{n}{4}, 0 \leq n \leq 11$ for $4 x$.
Of these numbers there are
- 3 integers $(0,1,2)$;
- 3 irreducible fractions with 2 as denominator (the numerators are $1,3,5$ );
- 6 irreducible fractions with 3 as denominator (the numerators are $1,2,4,5,7,8$ );
- 6 irreducible fractions with 4 as denominator (the numerators are $1,3,5,7,9,11,13,15$ );
- 4 irreducible fractions with 5 as denominator (the numerators are 3,6,9,12).
Therefore $f(x)$ increases 22 times per interval. Since $100=33 \cdot 3+1$, there are $33 \cdot 22$ changes of value in $[0,99)$. Finally, there are 8 more changes in [99,100]: 99, 100, $99 \frac{1}{2}, 99 \frac{1}{3}, 99 \frac{2}{3}, 99 \frac{1}{4}$, $99 \frac{3}{4}, 99 \frac{3}{5}$.
The total is then $33 \cdot 22+8=734$.
Comment: A more careful inspection shows that the range of $f$ are the numbers congruent modulo 35 to one of
$$
0,1,2,4,5,6,7,11,12,13,14,16,17,18,19,23,24,25,26,28,29,30
$$
in the interval $[0, f(100)]=[0,1166]$. Since $1166 \equiv 11(\bmod 35)$, this comprises 33 cycles plus the 8 numbers in the previous list.
|
{
"resource_path": "APMO/segmented/en-apmo1993_sol.jsonl",
"problem_match": "# Problem 2",
"solution_match": "# Solution\n\n"
}
|
bd5d8315-f23a-5686-b090-d21bea91e8e5
| 604,509
|
Let
$$
f(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+\cdots+a_{0} \quad \text { and } \quad g(x)=c_{n+1} x^{n+1}+c_{n} x^{n}+\cdots+c_{0}
$$
be non-zero polynomials with real coefficients such that $g(x)=(x+r) f(x)$ for some real number $r$. If $a=\max \left(\left|a_{n}\right|, \ldots,\left|a_{0}\right|\right)$ and $c=\max \left(\left|c_{n+1}\right|, \ldots,\left|c_{0}\right|\right)$, prove that $\frac{a}{c} \leq n+1$.
|
Expanding $(x+r) f(x)$, we find that $c_{n+1}=a_{n}, c_{k}=a_{k-1}+r a_{k}$ for $k=1,2, \ldots, n$, and $c_{0}=r a_{0}$. Consider three cases:
- $r=0$. Then $c_{0}=0$ and $c_{k}=a_{k-1}$ for $k=1,2, \ldots, n$, and $a=c \Longrightarrow \frac{a}{c}=1 \leq n+1$.
- $|r| \geq 1$. Then
$$
\begin{gathered}
\left|a_{0}\right|=\left|\frac{c_{0}}{r}\right| \leq c \\
\left|a_{1}\right|=\left|\frac{c_{1}-a_{0}}{r}\right| \leq\left|c_{1}\right|+\left|a_{0}\right| \leq 2 c
\end{gathered}
$$
and inductively if $\left|a_{k}\right| \leq(k+1) c$
$$
\left|a_{k+1}\right|=\left|\frac{c_{k+1}-a_{k}}{r}\right| \leq\left|c_{k+1}\right|+\left|a_{k}\right| \leq c+(k+1) c=(k+2) c
$$
Therefore, $\left|a_{k}\right| \leq(k+1) c \leq(n+1) c$ for all $k$, and $a \leq(n+1) c \Longleftrightarrow \frac{a}{c} \leq n+1$.
- $0<|r|<1$. Now work backwards: $\left|a_{n}\right|=\left|c_{n+1}\right| \leq c$,
$$
\left|a_{n-1}\right|=\left|c_{n}-r a_{n}\right| \leq\left|c_{n}\right|+\left|r a_{n}\right|<c+c=2 c,
$$
and inductively if $\left|a_{n-k}\right| \leq(k+1) c$
$$
\left|a_{n-k-1}\right|=\left|c_{n-k}-r a_{n-k}\right| \leq\left|c_{n-k}\right|+\left|r a_{n-k}\right|<c+(k+1) c=(k+2) c .
$$
Therefore, $\left|a_{n-k}\right| \leq(k+1) c \leq(n+1) c$ for all $k$, and $a \leq(n+1) c$ again.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let
$$
f(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+\cdots+a_{0} \quad \text { and } \quad g(x)=c_{n+1} x^{n+1}+c_{n} x^{n}+\cdots+c_{0}
$$
be non-zero polynomials with real coefficients such that $g(x)=(x+r) f(x)$ for some real number $r$. If $a=\max \left(\left|a_{n}\right|, \ldots,\left|a_{0}\right|\right)$ and $c=\max \left(\left|c_{n+1}\right|, \ldots,\left|c_{0}\right|\right)$, prove that $\frac{a}{c} \leq n+1$.
|
Expanding $(x+r) f(x)$, we find that $c_{n+1}=a_{n}, c_{k}=a_{k-1}+r a_{k}$ for $k=1,2, \ldots, n$, and $c_{0}=r a_{0}$. Consider three cases:
- $r=0$. Then $c_{0}=0$ and $c_{k}=a_{k-1}$ for $k=1,2, \ldots, n$, and $a=c \Longrightarrow \frac{a}{c}=1 \leq n+1$.
- $|r| \geq 1$. Then
$$
\begin{gathered}
\left|a_{0}\right|=\left|\frac{c_{0}}{r}\right| \leq c \\
\left|a_{1}\right|=\left|\frac{c_{1}-a_{0}}{r}\right| \leq\left|c_{1}\right|+\left|a_{0}\right| \leq 2 c
\end{gathered}
$$
and inductively if $\left|a_{k}\right| \leq(k+1) c$
$$
\left|a_{k+1}\right|=\left|\frac{c_{k+1}-a_{k}}{r}\right| \leq\left|c_{k+1}\right|+\left|a_{k}\right| \leq c+(k+1) c=(k+2) c
$$
Therefore, $\left|a_{k}\right| \leq(k+1) c \leq(n+1) c$ for all $k$, and $a \leq(n+1) c \Longleftrightarrow \frac{a}{c} \leq n+1$.
- $0<|r|<1$. Now work backwards: $\left|a_{n}\right|=\left|c_{n+1}\right| \leq c$,
$$
\left|a_{n-1}\right|=\left|c_{n}-r a_{n}\right| \leq\left|c_{n}\right|+\left|r a_{n}\right|<c+c=2 c,
$$
and inductively if $\left|a_{n-k}\right| \leq(k+1) c$
$$
\left|a_{n-k-1}\right|=\left|c_{n-k}-r a_{n-k}\right| \leq\left|c_{n-k}\right|+\left|r a_{n-k}\right|<c+(k+1) c=(k+2) c .
$$
Therefore, $\left|a_{n-k}\right| \leq(k+1) c \leq(n+1) c$ for all $k$, and $a \leq(n+1) c$ again.
|
{
"resource_path": "APMO/segmented/en-apmo1993_sol.jsonl",
"problem_match": "# Problem 3",
"solution_match": "# Solution\n\n"
}
|
620b5678-bb8e-5e62-b80e-3aa4b8fd846e
| 604,520
|
Determine all positive integers $n$ for which the equation
$$
x^{n}+(2+x)^{n}+(2-x)^{n}=0
$$
has an integer as a solution.
## Answer: $n=1$.
|
If $n$ is even, $x^{n}+(2+x)^{n}+(2-x)^{n}>0$, so $n$ is odd.
For $n=1$, the equation reduces to $x+(2+x)+(2-x)=0$, which has the unique solution $x=-4$.
For $n>1$, notice that $x$ is even, because $x, 2-x$, and $2+x$ have all the same parity. Let $x=2 y$, so the equation reduces to
$$
y^{n}+(1+y)^{n}+(1-y)^{n}=0 .
$$
Looking at this equation modulo 2 yields that $y+(1+y)+(1-y)=y+2$ is even, so $y$ is even. Using the factorization
$$
a^{n}+b^{n}=(a+b)\left(a^{n-1}-a^{n-2} b+\cdots+b^{n-1}\right) \quad \text { for } n \text { odd, }
$$
which has a sum of $n$ terms as the second factor, the equation is now equivalent to
$$
y^{n}+(1+y+1-y)\left((1+y)^{n-1}-(1+y)^{n-2}(1-y)+\cdots+(1-y)^{n-1}\right)=0
$$
or
$$
y^{n}=-2\left((1+y)^{n-1}-(1+y)^{n-2}(1-y)+\cdots+(1-y)^{n-1}\right) .
$$
Each of the $n$ terms in the second factor is odd, and $n$ is odd, so the second factor is odd. Therefore, $y^{n}$ has only one factor 2 , which is a contradiction to the fact that, $y$ being even, $y^{n}$ has at least $n>1$ factors 2 . Hence there are no solutions if $n>1$.
|
n=1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Determine all positive integers $n$ for which the equation
$$
x^{n}+(2+x)^{n}+(2-x)^{n}=0
$$
has an integer as a solution.
## Answer: $n=1$.
|
If $n$ is even, $x^{n}+(2+x)^{n}+(2-x)^{n}>0$, so $n$ is odd.
For $n=1$, the equation reduces to $x+(2+x)+(2-x)=0$, which has the unique solution $x=-4$.
For $n>1$, notice that $x$ is even, because $x, 2-x$, and $2+x$ have all the same parity. Let $x=2 y$, so the equation reduces to
$$
y^{n}+(1+y)^{n}+(1-y)^{n}=0 .
$$
Looking at this equation modulo 2 yields that $y+(1+y)+(1-y)=y+2$ is even, so $y$ is even. Using the factorization
$$
a^{n}+b^{n}=(a+b)\left(a^{n-1}-a^{n-2} b+\cdots+b^{n-1}\right) \quad \text { for } n \text { odd, }
$$
which has a sum of $n$ terms as the second factor, the equation is now equivalent to
$$
y^{n}+(1+y+1-y)\left((1+y)^{n-1}-(1+y)^{n-2}(1-y)+\cdots+(1-y)^{n-1}\right)=0
$$
or
$$
y^{n}=-2\left((1+y)^{n-1}-(1+y)^{n-2}(1-y)+\cdots+(1-y)^{n-1}\right) .
$$
Each of the $n$ terms in the second factor is odd, and $n$ is odd, so the second factor is odd. Therefore, $y^{n}$ has only one factor 2 , which is a contradiction to the fact that, $y$ being even, $y^{n}$ has at least $n>1$ factors 2 . Hence there are no solutions if $n>1$.
|
{
"resource_path": "APMO/segmented/en-apmo1993_sol.jsonl",
"problem_match": "# Problem 4",
"solution_match": "# Solution\n\n"
}
|
51da5931-dc98-5e7f-91f5-7f2175f9c9a1
| 604,531
|
Let $P_{1}, P_{2}, \ldots, P_{1993}=P_{0}$ be distinct points in the $x y$-plane with the following properties:
(i) both coordinates of $P_{i}$ are integers, for $i=1,2, \ldots, 1993$;
(ii) there is no point other than $P_{i}$ and $P_{i+1}$ on the line segment joining $P_{i}$ with $P_{i+1}$ whose coordinates are both integers, for $i=0,1, \ldots, 1992$.
Prove that for some $i, 0 \leq i \leq 1992$, there exists a point $Q$ with coordinates $\left(q_{x}, q_{y}\right)$ on the line segment joining $P_{i}$ with $P_{i+1}$ such that both $2 q_{x}$ and $2 q_{y}$ are odd integers.
|
Call a point $(x, y) \in \mathbb{Z}^{2}$ even or odd according to the parity of $x+y$. Since there are an odd number of points, there are two points $P_{i}=(a, b)$ and $P_{i+1}=(c, d), 0 \leq i \leq 1992$ with the same parity. This implies that $a+b+c+d$ is even. We claim that the midpoint of $P_{i} P_{i+1}$ is the desired point $Q$.
In fact, since $a+b+c+d=(a+c)+(b+d)$ is even, $a$ and $c$ have the same parity if and only if $b$ and $d$ also have the same parity. If both happen then the midpoint of $P_{i} P_{i+1}, Q=\left(\frac{a+c}{2}, \frac{b+d}{2}\right)$, has integer coordinates, which violates condition (ii). Then $a$ and $c$, as well as $b$ and $d$, have different parities, and $2 q_{x}=a+c$ and $2 q_{y}=b+d$ are both odd integers.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $P_{1}, P_{2}, \ldots, P_{1993}=P_{0}$ be distinct points in the $x y$-plane with the following properties:
(i) both coordinates of $P_{i}$ are integers, for $i=1,2, \ldots, 1993$;
(ii) there is no point other than $P_{i}$ and $P_{i+1}$ on the line segment joining $P_{i}$ with $P_{i+1}$ whose coordinates are both integers, for $i=0,1, \ldots, 1992$.
Prove that for some $i, 0 \leq i \leq 1992$, there exists a point $Q$ with coordinates $\left(q_{x}, q_{y}\right)$ on the line segment joining $P_{i}$ with $P_{i+1}$ such that both $2 q_{x}$ and $2 q_{y}$ are odd integers.
|
Call a point $(x, y) \in \mathbb{Z}^{2}$ even or odd according to the parity of $x+y$. Since there are an odd number of points, there are two points $P_{i}=(a, b)$ and $P_{i+1}=(c, d), 0 \leq i \leq 1992$ with the same parity. This implies that $a+b+c+d$ is even. We claim that the midpoint of $P_{i} P_{i+1}$ is the desired point $Q$.
In fact, since $a+b+c+d=(a+c)+(b+d)$ is even, $a$ and $c$ have the same parity if and only if $b$ and $d$ also have the same parity. If both happen then the midpoint of $P_{i} P_{i+1}, Q=\left(\frac{a+c}{2}, \frac{b+d}{2}\right)$, has integer coordinates, which violates condition (ii). Then $a$ and $c$, as well as $b$ and $d$, have different parities, and $2 q_{x}=a+c$ and $2 q_{y}=b+d$ are both odd integers.
|
{
"resource_path": "APMO/segmented/en-apmo1993_sol.jsonl",
"problem_match": "# Problem 5",
"solution_match": "# Solution\n\n"
}
|
7aa3067d-2293-5b49-8533-29510f81af65
| 604,546
|
Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be a function such that
(i) For all $x, y \in \mathbb{R}$,
$$
f(x)+f(y)+1 \geq f(x+y) \geq f(x)+f(y)
$$
(ii) For all $x \in[0,1), f(0) \geq f(x)$,
(iii) $-f(-1)=f(1)=1$.
Find all such functions $f$.
Answer: $f(x)=\lfloor x\rfloor$, the largest integer that does not exceed $x$, is the only function.
|
Plug $y \rightarrow 1$ in (i):
$$
f(x)+f(1)+1 \geq f(x+1) \geq f(x)+f(1) \Longleftrightarrow f(x)+1 \leq f(x+1) \leq f(x)+2
$$
Now plug $y \rightarrow-1$ and $x \rightarrow x+1$ in (i):
$$
f(x+1)+f(-1)+1 \geq f(x) \geq f(x+1)+f(-1) \Longleftrightarrow f(x) \leq f(x+1) \leq f(x)+1
$$
Hence $f(x+1)=f(x)+1$ and we only need to define $f(x)$ on $[0,1)$. Note that $f(1)=$ $f(0)+1 \Longrightarrow f(0)=0$.
Condition (ii) states that $f(x) \leq 0$ in $[0,1)$.
Now plug $y \rightarrow 1-x$ in (i):
$$
f(x)+f(1-x)+1 \leq f(x+(1-x)) \leq f(x)+f(1-x) \Longrightarrow f(x)+f(1-x) \geq 0
$$
If $x \in(0,1)$ then $1-x \in(0,1)$ as well, so $f(x) \leq 0$ and $f(1-x) \leq 0$, which implies $f(x)+f(1-x) \leq 0$. Thus, $f(x)=f(1-x)=0$ for $x \in(0,1)$. This combined with $f(0)=0$ and $f(x+1)=f(x)+1$ proves that $f(x)=\lfloor x\rfloor$, which satisfies the problem conditions, as since
$x+y=\lfloor x\rfloor+\lfloor y\rfloor+\{x\}+\{y\}$ and $0 \leq\{x\}+\{y\}<2 \Longrightarrow\lfloor x\rfloor+\lfloor y\rfloor \leq x+y<\lfloor x\rfloor+\lfloor y\rfloor+2$ implies
$$
\lfloor x\rfloor+\lfloor y\rfloor+1 \geq\lfloor x+y\rfloor \geq\lfloor x\rfloor+\lfloor y\rfloor .
$$
|
f(x)=\lfloor x\rfloor
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be a function such that
(i) For all $x, y \in \mathbb{R}$,
$$
f(x)+f(y)+1 \geq f(x+y) \geq f(x)+f(y)
$$
(ii) For all $x \in[0,1), f(0) \geq f(x)$,
(iii) $-f(-1)=f(1)=1$.
Find all such functions $f$.
Answer: $f(x)=\lfloor x\rfloor$, the largest integer that does not exceed $x$, is the only function.
|
Plug $y \rightarrow 1$ in (i):
$$
f(x)+f(1)+1 \geq f(x+1) \geq f(x)+f(1) \Longleftrightarrow f(x)+1 \leq f(x+1) \leq f(x)+2
$$
Now plug $y \rightarrow-1$ and $x \rightarrow x+1$ in (i):
$$
f(x+1)+f(-1)+1 \geq f(x) \geq f(x+1)+f(-1) \Longleftrightarrow f(x) \leq f(x+1) \leq f(x)+1
$$
Hence $f(x+1)=f(x)+1$ and we only need to define $f(x)$ on $[0,1)$. Note that $f(1)=$ $f(0)+1 \Longrightarrow f(0)=0$.
Condition (ii) states that $f(x) \leq 0$ in $[0,1)$.
Now plug $y \rightarrow 1-x$ in (i):
$$
f(x)+f(1-x)+1 \leq f(x+(1-x)) \leq f(x)+f(1-x) \Longrightarrow f(x)+f(1-x) \geq 0
$$
If $x \in(0,1)$ then $1-x \in(0,1)$ as well, so $f(x) \leq 0$ and $f(1-x) \leq 0$, which implies $f(x)+f(1-x) \leq 0$. Thus, $f(x)=f(1-x)=0$ for $x \in(0,1)$. This combined with $f(0)=0$ and $f(x+1)=f(x)+1$ proves that $f(x)=\lfloor x\rfloor$, which satisfies the problem conditions, as since
$x+y=\lfloor x\rfloor+\lfloor y\rfloor+\{x\}+\{y\}$ and $0 \leq\{x\}+\{y\}<2 \Longrightarrow\lfloor x\rfloor+\lfloor y\rfloor \leq x+y<\lfloor x\rfloor+\lfloor y\rfloor+2$ implies
$$
\lfloor x\rfloor+\lfloor y\rfloor+1 \geq\lfloor x+y\rfloor \geq\lfloor x\rfloor+\lfloor y\rfloor .
$$
|
{
"resource_path": "APMO/segmented/en-apmo1994_sol.jsonl",
"problem_match": "# Problem 1",
"solution_match": "# Solution\n\n"
}
|
9b88506d-f827-57a8-9e89-f6da2f669f01
| 604,557
|
Given a nondegenerate triangle $A B C$, with circumcentre $O$, orthocentre $H$, and circumradius $R$, prove that $|O H|<3 R$.
|
Embed $A B C$ in the complex plane, with $A, B$ and $C$ in the circle $|z|=R$, so $O$ is the origin. Represent each point by its lowercase letter. It is well known that $h=a+b+c$, so
$$
O H=|a+b+c| \leq|a|+|b|+|c|=3 R .
$$
The equality cannot occur because $a, b$, and $c$ are not collinear, so $O H<3 R$.
|
O H<3 R
|
Yes
|
Yes
|
proof
|
Geometry
|
Given a nondegenerate triangle $A B C$, with circumcentre $O$, orthocentre $H$, and circumradius $R$, prove that $|O H|<3 R$.
|
Embed $A B C$ in the complex plane, with $A, B$ and $C$ in the circle $|z|=R$, so $O$ is the origin. Represent each point by its lowercase letter. It is well known that $h=a+b+c$, so
$$
O H=|a+b+c| \leq|a|+|b|+|c|=3 R .
$$
The equality cannot occur because $a, b$, and $c$ are not collinear, so $O H<3 R$.
|
{
"resource_path": "APMO/segmented/en-apmo1994_sol.jsonl",
"problem_match": "# Problem 2",
"solution_match": "# Solution 1"
}
|
392d101e-6071-52b8-9672-760a0d3498f8
| 604,567
|
Given a nondegenerate triangle $A B C$, with circumcentre $O$, orthocentre $H$, and circumradius $R$, prove that $|O H|<3 R$.
|
Suppose with loss of generality that $\angle A<90^{\circ}$. Let $B D$ be an altitude. Then
$$
A H=\frac{A D}{\cos \left(90^{\circ}-C\right)}=\frac{A B \cos A}{\sin C}=2 R \cos A
$$
By the triangle inequality,
$$
O H<A O+A H=R+2 R \cos A<3 R
$$
Comment: With a bit more work, if $a, b, c$ are the sidelengths of $A B C$, one can show that
$$
O H^{2}=9 R^{2}-a^{2}-b^{2}-c^{2} .
$$
In fact, using vectors in a coordinate system with $O$ as origin, by the Euler line
$$
\overrightarrow{O H}=3 \overrightarrow{O G}=3 \cdot \frac{\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}}{3}=\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}
$$
so
$$
O H^{2}=\overrightarrow{O H} \cdot \overrightarrow{O H}=(\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}) \cdot(\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C})
$$
Expanding and using the fact that $\overrightarrow{O X} \cdot \overrightarrow{O X}=O X^{2}=R^{2}$ for $X \in\{A, B, C\}$, as well as
$\overrightarrow{O A} \cdot \overrightarrow{O B}=O A \cdot O B \cdot \cos \angle A O B=R^{2} \cos 2 C=R^{2}\left(1-2 \sin ^{2} C\right)=R^{2}\left(1-2\left(\frac{c}{2 R}\right)^{2}\right)=R^{2}-\frac{c^{2}}{2}$, we find that
$$
\begin{aligned}
O H^{2} & =\overrightarrow{O A} \cdot \overrightarrow{O A}+\overrightarrow{O B} \cdot \overrightarrow{O B}+\overrightarrow{O C} \cdot \overrightarrow{O C}+2 \overrightarrow{O A} \cdot \overrightarrow{O B}+2 \overrightarrow{O A} \cdot \overrightarrow{O C}+2 \overrightarrow{O B} \cdot \overrightarrow{O C} \\
& =3 R^{2}+\left(2 R^{2}-c^{2}\right)+\left(2 R^{2}-b^{2}\right)+\left(2 R^{2}-a^{2}\right) \\
& =9 R^{2}-a^{2}-b^{2}-c^{2}
\end{aligned}
$$
as required.
This proves that $O H^{2}<9 R^{2} \Longrightarrow O H<3 R$, and since $a, b, c$ can be arbitrarily small (fix the circumcircle and choose $A, B, C$ arbitrarily close in this circle), the bound is sharp.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Given a nondegenerate triangle $A B C$, with circumcentre $O$, orthocentre $H$, and circumradius $R$, prove that $|O H|<3 R$.
|
Suppose with loss of generality that $\angle A<90^{\circ}$. Let $B D$ be an altitude. Then
$$
A H=\frac{A D}{\cos \left(90^{\circ}-C\right)}=\frac{A B \cos A}{\sin C}=2 R \cos A
$$
By the triangle inequality,
$$
O H<A O+A H=R+2 R \cos A<3 R
$$
Comment: With a bit more work, if $a, b, c$ are the sidelengths of $A B C$, one can show that
$$
O H^{2}=9 R^{2}-a^{2}-b^{2}-c^{2} .
$$
In fact, using vectors in a coordinate system with $O$ as origin, by the Euler line
$$
\overrightarrow{O H}=3 \overrightarrow{O G}=3 \cdot \frac{\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}}{3}=\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}
$$
so
$$
O H^{2}=\overrightarrow{O H} \cdot \overrightarrow{O H}=(\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}) \cdot(\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C})
$$
Expanding and using the fact that $\overrightarrow{O X} \cdot \overrightarrow{O X}=O X^{2}=R^{2}$ for $X \in\{A, B, C\}$, as well as
$\overrightarrow{O A} \cdot \overrightarrow{O B}=O A \cdot O B \cdot \cos \angle A O B=R^{2} \cos 2 C=R^{2}\left(1-2 \sin ^{2} C\right)=R^{2}\left(1-2\left(\frac{c}{2 R}\right)^{2}\right)=R^{2}-\frac{c^{2}}{2}$, we find that
$$
\begin{aligned}
O H^{2} & =\overrightarrow{O A} \cdot \overrightarrow{O A}+\overrightarrow{O B} \cdot \overrightarrow{O B}+\overrightarrow{O C} \cdot \overrightarrow{O C}+2 \overrightarrow{O A} \cdot \overrightarrow{O B}+2 \overrightarrow{O A} \cdot \overrightarrow{O C}+2 \overrightarrow{O B} \cdot \overrightarrow{O C} \\
& =3 R^{2}+\left(2 R^{2}-c^{2}\right)+\left(2 R^{2}-b^{2}\right)+\left(2 R^{2}-a^{2}\right) \\
& =9 R^{2}-a^{2}-b^{2}-c^{2}
\end{aligned}
$$
as required.
This proves that $O H^{2}<9 R^{2} \Longrightarrow O H<3 R$, and since $a, b, c$ can be arbitrarily small (fix the circumcircle and choose $A, B, C$ arbitrarily close in this circle), the bound is sharp.
|
{
"resource_path": "APMO/segmented/en-apmo1994_sol.jsonl",
"problem_match": "# Problem 2",
"solution_match": "# Solution 2"
}
|
392d101e-6071-52b8-9672-760a0d3498f8
| 604,567
|
Let $n$ be an integer of the form $a^{2}+b^{2}$, where $a$ and $b$ are relatively prime integers and such that if $p$ is a prime, $p \leq \sqrt{n}$, then $p$ divides $a b$. Determine all such $n$.
Answer: $n=2,5,13$.
|
A prime $p$ divides $a b$ if and only if divides either $a$ or $b$. If $n=a^{2}+b^{2}$ is a composite then it has a prime divisor $p \leq \sqrt{n}$, and if $p$ divides $a$ it divides $b$ and vice-versa, which is not possible because $a$ and $b$ are coprime. Therefore $n$ is a prime.
Suppose without loss of generality that $a \geq b$ and consider $a-b$. Note that $a^{2}+b^{2}=(a-b)^{2}+2 a b$.
- If $a=b$ then $a=b=1$ because $a$ and $b$ are coprime. $n=2$ is a solution.
- If $a-b=1$ then $a$ and $b$ are coprime and $a^{2}+b^{2}=(a-b)^{2}+2 a b=2 a b+1=2 b(b+1)+1=$ $2 b^{2}+2 b+1$. So any prime factor of any number smaller than $\sqrt{2 b^{2}+2 b+1}$ is a divisor of $a b=b(b+1)$.
One can check that $b=1$ and $b=2$ yields the solutions $n=1^{2}+2^{2}=5$ (the only prime $p$ is 2 ) and $n=2^{2}+3^{2}=13$ (the only primes $p$ are 2 and 3 ). Suppose that $b>2$.
Consider, for instance, the prime factors of $b-1 \leq \sqrt{2 b^{2}+2 b+1}$, which is coprime with $b$. Any prime must then divide $a=b+1$. Then it divides $(b+1)-(b-1)=2$, that is, $b-1$ can only have 2 as a prime factor, that is, $b-1$ is a power of 2 , and since $b-1 \geq 2$, $b$ is odd.
Since $2 b^{2}+2 b+1-(b+2)^{2}=b^{2}-2 b-3=(b-3)(b+1) \geq 0$, we can also consider any prime divisor of $b+2$. Since $b$ is odd, $b$ and $b+2$ are also coprime, so any prime divisor of $b+2$ must divide $a=b+1$. But $b+1$ and $b+2$ are also coprime, so there can be no such primes. This is a contradiction, and $b \geq 3$ does not yield any solutions.
- If $a-b>1$, consider a prime divisor $p$ of $a-b=\sqrt{a^{2}-2 a b+b^{2}}<\sqrt{a^{2}+b^{2}}$. Since $p$ divides one of $a$ and $b, p$ divides both numbers (just add or subtract $a-b$ accordingly.) This is a contradiction.
Hence the only solutions are $n=2,5,13$.
|
n=2,5,13
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $n$ be an integer of the form $a^{2}+b^{2}$, where $a$ and $b$ are relatively prime integers and such that if $p$ is a prime, $p \leq \sqrt{n}$, then $p$ divides $a b$. Determine all such $n$.
Answer: $n=2,5,13$.
|
A prime $p$ divides $a b$ if and only if divides either $a$ or $b$. If $n=a^{2}+b^{2}$ is a composite then it has a prime divisor $p \leq \sqrt{n}$, and if $p$ divides $a$ it divides $b$ and vice-versa, which is not possible because $a$ and $b$ are coprime. Therefore $n$ is a prime.
Suppose without loss of generality that $a \geq b$ and consider $a-b$. Note that $a^{2}+b^{2}=(a-b)^{2}+2 a b$.
- If $a=b$ then $a=b=1$ because $a$ and $b$ are coprime. $n=2$ is a solution.
- If $a-b=1$ then $a$ and $b$ are coprime and $a^{2}+b^{2}=(a-b)^{2}+2 a b=2 a b+1=2 b(b+1)+1=$ $2 b^{2}+2 b+1$. So any prime factor of any number smaller than $\sqrt{2 b^{2}+2 b+1}$ is a divisor of $a b=b(b+1)$.
One can check that $b=1$ and $b=2$ yields the solutions $n=1^{2}+2^{2}=5$ (the only prime $p$ is 2 ) and $n=2^{2}+3^{2}=13$ (the only primes $p$ are 2 and 3 ). Suppose that $b>2$.
Consider, for instance, the prime factors of $b-1 \leq \sqrt{2 b^{2}+2 b+1}$, which is coprime with $b$. Any prime must then divide $a=b+1$. Then it divides $(b+1)-(b-1)=2$, that is, $b-1$ can only have 2 as a prime factor, that is, $b-1$ is a power of 2 , and since $b-1 \geq 2$, $b$ is odd.
Since $2 b^{2}+2 b+1-(b+2)^{2}=b^{2}-2 b-3=(b-3)(b+1) \geq 0$, we can also consider any prime divisor of $b+2$. Since $b$ is odd, $b$ and $b+2$ are also coprime, so any prime divisor of $b+2$ must divide $a=b+1$. But $b+1$ and $b+2$ are also coprime, so there can be no such primes. This is a contradiction, and $b \geq 3$ does not yield any solutions.
- If $a-b>1$, consider a prime divisor $p$ of $a-b=\sqrt{a^{2}-2 a b+b^{2}}<\sqrt{a^{2}+b^{2}}$. Since $p$ divides one of $a$ and $b, p$ divides both numbers (just add or subtract $a-b$ accordingly.) This is a contradiction.
Hence the only solutions are $n=2,5,13$.
|
{
"resource_path": "APMO/segmented/en-apmo1994_sol.jsonl",
"problem_match": "# Problem 3",
"solution_match": "# Solution\n\n"
}
|
0726ccb1-20f7-560b-94c6-95b76c5a5289
| 604,592
|
Is there an infinite set of points in the plane such that no three points are collinear, and the distance between any two points is rational?
Answer: Yes.
|
The answer is yes and we present the following construction: the idea is considering points in the unit circle of the form $P_{n}=(\cos (2 n \theta), \sin (2 n \theta))$ for an appropriate $\theta$. Then the distance $P_{m} P_{n}$ is the length of the chord with central angle $(2 m-2 n) \theta \bmod \pi$, that is, $2|\sin ((m-n) \theta)|$. Our task is then finding $\theta$ such that (i) $\sin (k \theta)$ is rational for all $k \in \mathbb{Z}$; (ii) points $P_{n}$ are all distinct. We claim that $\theta \in(0, \pi / 2)$ such that $\cos \theta=\frac{3}{5}$ and therefore $\sin \theta=\frac{4}{5}$ does the job. Proof of (i): We know that $\sin ((n+1) \theta)+\sin ((n-1) \theta)=2 \sin (n \theta) \cos \theta$, so if $\sin ((n-1) \theta$ and $\sin (n \theta)$ are both rational then $\sin ((n+1) \theta)$ also is. Since $\sin (0 \theta)=0$ and $\sin \theta$ are rational, an induction shows that $\sin (n \theta)$ is rational for $n \in \mathbb{Z}_{>0}$; the result is also true if $n$ is negative because $\sin$ is an odd function.
Proof of (ii): $P_{m}=P_{n} \Longleftrightarrow 2 n \theta=2 m \theta+2 k \pi$ for some $k \in \mathbb{Z}$, which implies $\sin ((n-m) \theta)=$ $\sin (k \pi)=0$. We show that $\sin (k \theta) \neq 0$ for all $k \neq 0$.
We prove a stronger result: let $\sin (k \theta)=\frac{a_{k}}{5^{k}}$. Then
$$
\begin{aligned}
\sin ((k+1) \theta)+\sin ((k-1) \theta)=2 \sin (k \theta) \cos \theta & \Longleftrightarrow \frac{a_{k+1}}{5^{k+1}}+\frac{a_{k-1}}{5^{k-1}}=2 \cdot \frac{a_{k}}{5^{k}} \cdot \frac{3}{5} \\
& \Longleftrightarrow a_{k+1}=6 a_{k}-25 a_{k-1}
\end{aligned}
$$
Since $a_{0}=0$ and $a_{1}=4, a_{k}$ is an integer for $k \geq 0$, and $a_{k+1} \equiv a_{k}(\bmod 5)$ for $k \geq 1$ (note that $a_{-1}=-\frac{4}{25}$ is not an integer!). Thus $a_{k} \equiv 4(\bmod 5)$ for all $k \geq 1$, and $\sin (k \theta)=\frac{a_{k}}{5^{k}}$ is an irreducible fraction with $5^{k}$ as denominator and $a_{k} \equiv 4(\bmod 5)$. This proves (ii) and we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Is there an infinite set of points in the plane such that no three points are collinear, and the distance between any two points is rational?
Answer: Yes.
|
The answer is yes and we present the following construction: the idea is considering points in the unit circle of the form $P_{n}=(\cos (2 n \theta), \sin (2 n \theta))$ for an appropriate $\theta$. Then the distance $P_{m} P_{n}$ is the length of the chord with central angle $(2 m-2 n) \theta \bmod \pi$, that is, $2|\sin ((m-n) \theta)|$. Our task is then finding $\theta$ such that (i) $\sin (k \theta)$ is rational for all $k \in \mathbb{Z}$; (ii) points $P_{n}$ are all distinct. We claim that $\theta \in(0, \pi / 2)$ such that $\cos \theta=\frac{3}{5}$ and therefore $\sin \theta=\frac{4}{5}$ does the job. Proof of (i): We know that $\sin ((n+1) \theta)+\sin ((n-1) \theta)=2 \sin (n \theta) \cos \theta$, so if $\sin ((n-1) \theta$ and $\sin (n \theta)$ are both rational then $\sin ((n+1) \theta)$ also is. Since $\sin (0 \theta)=0$ and $\sin \theta$ are rational, an induction shows that $\sin (n \theta)$ is rational for $n \in \mathbb{Z}_{>0}$; the result is also true if $n$ is negative because $\sin$ is an odd function.
Proof of (ii): $P_{m}=P_{n} \Longleftrightarrow 2 n \theta=2 m \theta+2 k \pi$ for some $k \in \mathbb{Z}$, which implies $\sin ((n-m) \theta)=$ $\sin (k \pi)=0$. We show that $\sin (k \theta) \neq 0$ for all $k \neq 0$.
We prove a stronger result: let $\sin (k \theta)=\frac{a_{k}}{5^{k}}$. Then
$$
\begin{aligned}
\sin ((k+1) \theta)+\sin ((k-1) \theta)=2 \sin (k \theta) \cos \theta & \Longleftrightarrow \frac{a_{k+1}}{5^{k+1}}+\frac{a_{k-1}}{5^{k-1}}=2 \cdot \frac{a_{k}}{5^{k}} \cdot \frac{3}{5} \\
& \Longleftrightarrow a_{k+1}=6 a_{k}-25 a_{k-1}
\end{aligned}
$$
Since $a_{0}=0$ and $a_{1}=4, a_{k}$ is an integer for $k \geq 0$, and $a_{k+1} \equiv a_{k}(\bmod 5)$ for $k \geq 1$ (note that $a_{-1}=-\frac{4}{25}$ is not an integer!). Thus $a_{k} \equiv 4(\bmod 5)$ for all $k \geq 1$, and $\sin (k \theta)=\frac{a_{k}}{5^{k}}$ is an irreducible fraction with $5^{k}$ as denominator and $a_{k} \equiv 4(\bmod 5)$. This proves (ii) and we are done.
|
{
"resource_path": "APMO/segmented/en-apmo1994_sol.jsonl",
"problem_match": "# Problem 4",
"solution_match": "# Solution 1"
}
|
1b841da3-cad4-5ef6-90dc-95513070c396
| 604,608
|
Is there an infinite set of points in the plane such that no three points are collinear, and the distance between any two points is rational?
Answer: Yes.
|
We present a different construction. Consider the (collinear) points
$$
P_{k}=\left(1, \frac{x_{k}}{y_{k}}\right),
$$
such that the distance $O P_{k}$ from the origin $O$,
$$
O P_{k}=\frac{\sqrt{x_{k}^{2}+y_{k}^{2}}}{y_{k}}
$$
is rational, and $x_{k}$ and $y_{k}$ are integers. Clearly, $P_{i} P_{j}=\left|\frac{x_{i}}{y_{i}}-\frac{x_{j}}{y_{j}}\right|$ is rational.
Perform an inversion with center $O$ and unit radius. It maps the line $x=1$, which contains all points $P_{k}$, to a circle (minus the origin). Let $Q_{k}$ be the image of $P_{k}$ under this inversion. Then
$$
Q_{i} Q_{j}=\frac{1^{2} P_{i} P_{j}}{O P_{i} \cdot O P_{j}}
$$
is rational and we are done if we choose $x_{k}$ and $y_{k}$ accordingly. But this is not hard, as we can choose the legs of a Pythagorean triple, say
$$
x_{k}=k^{2}-1, \quad y_{k}=2 k
$$
This implies $O P_{k}=\frac{k^{2}+1}{2 k}$, and then
$$
Q_{i} Q_{j}=\frac{\left|\frac{i^{2}-1}{i}-\frac{j^{2}-1}{j}\right|}{\frac{i^{2}+1}{2 i} \cdot \frac{j^{2}+1}{2 j}}=\frac{|4(i-j)(i j+1)|}{\left(i^{2}+1\right)\left(j^{2}+1\right)}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Is there an infinite set of points in the plane such that no three points are collinear, and the distance between any two points is rational?
Answer: Yes.
|
We present a different construction. Consider the (collinear) points
$$
P_{k}=\left(1, \frac{x_{k}}{y_{k}}\right),
$$
such that the distance $O P_{k}$ from the origin $O$,
$$
O P_{k}=\frac{\sqrt{x_{k}^{2}+y_{k}^{2}}}{y_{k}}
$$
is rational, and $x_{k}$ and $y_{k}$ are integers. Clearly, $P_{i} P_{j}=\left|\frac{x_{i}}{y_{i}}-\frac{x_{j}}{y_{j}}\right|$ is rational.
Perform an inversion with center $O$ and unit radius. It maps the line $x=1$, which contains all points $P_{k}$, to a circle (minus the origin). Let $Q_{k}$ be the image of $P_{k}$ under this inversion. Then
$$
Q_{i} Q_{j}=\frac{1^{2} P_{i} P_{j}}{O P_{i} \cdot O P_{j}}
$$
is rational and we are done if we choose $x_{k}$ and $y_{k}$ accordingly. But this is not hard, as we can choose the legs of a Pythagorean triple, say
$$
x_{k}=k^{2}-1, \quad y_{k}=2 k
$$
This implies $O P_{k}=\frac{k^{2}+1}{2 k}$, and then
$$
Q_{i} Q_{j}=\frac{\left|\frac{i^{2}-1}{i}-\frac{j^{2}-1}{j}\right|}{\frac{i^{2}+1}{2 i} \cdot \frac{j^{2}+1}{2 j}}=\frac{|4(i-j)(i j+1)|}{\left(i^{2}+1\right)\left(j^{2}+1\right)}
$$
|
{
"resource_path": "APMO/segmented/en-apmo1994_sol.jsonl",
"problem_match": "# Problem 4",
"solution_match": "# Solution 2"
}
|
1b841da3-cad4-5ef6-90dc-95513070c396
| 604,608
|
You are given three lists $A, B$, and $C$. List $A$ contains the numbers of the form $10^{k}$ in base 10, with $k$ any integer greater than or equal to 1 . Lists $B$ and $C$ contain the same numbers translated into base 2 and 5 respectively:
| $A$ | $B$ | $C$ |
| :--- | :--- | :--- |
| 10 | 1010 | 20 |
| 100 | 1100100 | 400 |
| 1000 | 1111101000 | 13000 |
| $\vdots$ | $\vdots$ | $\vdots$ |
Prove that for every integer $n>1$, there is exactly one number in exactly one of the lists $B$ or $C$ that has exactly $n$ digits.
|
Let $b_{k}$ and $c_{k}$ be the number of digits in the $k$ th term in lists $B$ and $C$, respectively. Then
$$
2^{b_{k}-1} \leq 10^{k}<2^{b_{k}} \Longleftrightarrow \log _{2} 10^{k}<b_{k} \leq \log _{2} 10^{k}+1 \Longleftrightarrow b_{k}=\left\lfloor k \cdot \log _{2} 10\right\rfloor+1
$$
and, similarly
$$
c_{k}=\left\lfloor k \cdot \log _{5} 10\right\rfloor+1
$$
Beatty's theorem states that if $\alpha$ and $\beta$ are irrational positive numbers such that
$$
\frac{1}{\alpha}+\frac{1}{\beta}=1
$$
then the sequences $\lfloor k \alpha\rfloor$ and $\lfloor k \beta\rfloor, k=1,2, \ldots$, partition the positive integers.
Then, since
$$
\frac{1}{\log _{2} 10}+\frac{1}{\log _{5} 10}=\log _{10} 2+\log _{10} 5=\log _{10}(2 \cdot 5)=1
$$
the sequences $b_{k}-1$ and $c_{k}-1$ partition the positive integers, and therefore each integer greater than 1 appears in $b_{k}$ or $c_{k}$ exactly once. We are done.
Comment: For the sake of completeness, a proof of Beatty's theorem follows.
Let $x_{n}=\alpha n$ and $y_{n}=\beta n, n \geq 1$ integer. Note that, since $\alpha m=\beta n$ implies that $\frac{\alpha}{\beta}$ is rational but
$$
\frac{\alpha}{\beta}=\alpha \cdot \frac{1}{\beta}=\alpha\left(1-\frac{1}{\alpha}\right)=\alpha-1
$$
is irrational, the sequences have no common terms, and all terms in both sequences are irrational.
The theorem is equivalent to proving that exactly one term of either $x_{n}$ of $y_{n}$ lies in the interval $(N, N+1)$ for each $N$ positive integer. For that purpose we count the number of terms of the union of the two sequences in the interval $(0, N)$ : since $n \alpha<N \Longleftrightarrow n<\frac{N}{\alpha}$, there are $\left\lfloor\frac{N}{\alpha}\right\rfloor$ terms of $x_{n}$ in the interval and, similarly, $\left\lfloor\frac{N}{\beta}\right\rfloor$ terms of $y_{n}$ in the same interval. Since the sequences are disjoint, the total of numbers is
$$
T(N)=\left\lfloor\frac{N}{\alpha}\right\rfloor+\left\lfloor\frac{N}{\beta}\right\rfloor
$$
However, $x-1<\lfloor x\rfloor<x$ for nonintegers $x$, so
$$
\begin{aligned}
\frac{N}{\alpha}-1+\frac{N}{\beta}-1<T(N)<\frac{N}{\alpha}+\frac{N}{\beta} & \Longleftrightarrow N\left(\frac{1}{\alpha}+\frac{1}{\beta}\right)-2<T(N)<N\left(\frac{1}{\alpha}+\frac{1}{\beta}\right) \\
& \Longleftrightarrow N-2<T(N)<N,
\end{aligned}
$$
that is, $T(N)=N-1$.
Therefore the number of terms in $(N, N+1)$ is $T(N+1)-T(N)=N-(N-1)=1$, and the result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
You are given three lists $A, B$, and $C$. List $A$ contains the numbers of the form $10^{k}$ in base 10, with $k$ any integer greater than or equal to 1 . Lists $B$ and $C$ contain the same numbers translated into base 2 and 5 respectively:
| $A$ | $B$ | $C$ |
| :--- | :--- | :--- |
| 10 | 1010 | 20 |
| 100 | 1100100 | 400 |
| 1000 | 1111101000 | 13000 |
| $\vdots$ | $\vdots$ | $\vdots$ |
Prove that for every integer $n>1$, there is exactly one number in exactly one of the lists $B$ or $C$ that has exactly $n$ digits.
|
Let $b_{k}$ and $c_{k}$ be the number of digits in the $k$ th term in lists $B$ and $C$, respectively. Then
$$
2^{b_{k}-1} \leq 10^{k}<2^{b_{k}} \Longleftrightarrow \log _{2} 10^{k}<b_{k} \leq \log _{2} 10^{k}+1 \Longleftrightarrow b_{k}=\left\lfloor k \cdot \log _{2} 10\right\rfloor+1
$$
and, similarly
$$
c_{k}=\left\lfloor k \cdot \log _{5} 10\right\rfloor+1
$$
Beatty's theorem states that if $\alpha$ and $\beta$ are irrational positive numbers such that
$$
\frac{1}{\alpha}+\frac{1}{\beta}=1
$$
then the sequences $\lfloor k \alpha\rfloor$ and $\lfloor k \beta\rfloor, k=1,2, \ldots$, partition the positive integers.
Then, since
$$
\frac{1}{\log _{2} 10}+\frac{1}{\log _{5} 10}=\log _{10} 2+\log _{10} 5=\log _{10}(2 \cdot 5)=1
$$
the sequences $b_{k}-1$ and $c_{k}-1$ partition the positive integers, and therefore each integer greater than 1 appears in $b_{k}$ or $c_{k}$ exactly once. We are done.
Comment: For the sake of completeness, a proof of Beatty's theorem follows.
Let $x_{n}=\alpha n$ and $y_{n}=\beta n, n \geq 1$ integer. Note that, since $\alpha m=\beta n$ implies that $\frac{\alpha}{\beta}$ is rational but
$$
\frac{\alpha}{\beta}=\alpha \cdot \frac{1}{\beta}=\alpha\left(1-\frac{1}{\alpha}\right)=\alpha-1
$$
is irrational, the sequences have no common terms, and all terms in both sequences are irrational.
The theorem is equivalent to proving that exactly one term of either $x_{n}$ of $y_{n}$ lies in the interval $(N, N+1)$ for each $N$ positive integer. For that purpose we count the number of terms of the union of the two sequences in the interval $(0, N)$ : since $n \alpha<N \Longleftrightarrow n<\frac{N}{\alpha}$, there are $\left\lfloor\frac{N}{\alpha}\right\rfloor$ terms of $x_{n}$ in the interval and, similarly, $\left\lfloor\frac{N}{\beta}\right\rfloor$ terms of $y_{n}$ in the same interval. Since the sequences are disjoint, the total of numbers is
$$
T(N)=\left\lfloor\frac{N}{\alpha}\right\rfloor+\left\lfloor\frac{N}{\beta}\right\rfloor
$$
However, $x-1<\lfloor x\rfloor<x$ for nonintegers $x$, so
$$
\begin{aligned}
\frac{N}{\alpha}-1+\frac{N}{\beta}-1<T(N)<\frac{N}{\alpha}+\frac{N}{\beta} & \Longleftrightarrow N\left(\frac{1}{\alpha}+\frac{1}{\beta}\right)-2<T(N)<N\left(\frac{1}{\alpha}+\frac{1}{\beta}\right) \\
& \Longleftrightarrow N-2<T(N)<N,
\end{aligned}
$$
that is, $T(N)=N-1$.
Therefore the number of terms in $(N, N+1)$ is $T(N+1)-T(N)=N-(N-1)=1$, and the result follows.
|
{
"resource_path": "APMO/segmented/en-apmo1994_sol.jsonl",
"problem_match": "# Problem 5",
"solution_match": "# Solution\n\n"
}
|
2c3fb340-39e9-52e3-a2a8-1aeebdcc1da4
| 604,631
|
Find the smallest positive integer $n$ with the following property : There does not exist an arithmetic progression of 1993 terms of real numbers containing exactly $n$ integers.
|
and Marking Scheme:
We first note that the integer terms of any arithmetic progression are "equally spaced", because if the $i$ th term $a_{i}$ and the $(i+j)$ th term $a_{i+j}$ of an arithmetic progression are both integers, then so is the $(i+2 j)$ th term $a_{i+2 j}=a_{i+j}+\left(a_{i+j}-a_{i}\right)$.
1 POINT for realizing that the integers must be "equally spaced".
Thus, by scaling and translation, we can assume that the integer terms of the arithmetic progression are $1,2, \cdots, n$ and we need only to consider arithmetic progression of the form
$$
1,1+\frac{1}{k}, 1+\frac{2}{k}, \cdots, 1+\frac{k-1}{k}, 2,2+\frac{1}{k}, \cdots, n-1, \cdots, n-1+\frac{k-1}{k}, n
$$
This has $k n-k+1$ terms of which exactly $n$ are integers. Moreover we can add up to $k-1$ terms on either end and get another arithmetic progression without changing the number of integer terms.
2 POINTS for noticing that the maximal sequence has an equal number of terms on either side of the integers appearing in the sequence (this includes the 1 POINT above). In other words, 2 POINTS for the scaled and translated form of the progression including the $k-1$ terms on either side.
Thus there are arithmetic progressions with $n$ integers whose length is any integer lying in the interval $[k n-k+1, k n+k-1]$, where $k$ is any positive integer. Thus we want to find the smallest $n>0$ so that, if $k$ is the largest integer satisfying $k n+k-1 \leq 1998$, then $(k+1) n-(k+1)+1 \geq 2000$.
4 POINTS for clarifying the nature of the number $n$ in this way, which includes counting the terms of the maximal and minimal sequences containing $n$ integers and bounding them accordingly (this includes the 2 POINTS above).
That is, putting $k=\lfloor 1999 /(n+1)\rfloor$, we want the smallest integer $n$ so that
$$
\left\lfloor\frac{1999}{n+1}\right\rfloor(n-1)+n \geq 2000
$$
This inequality does not hold if
$$
\frac{1999}{n+1} \cdot(n-1)+n<2000
$$
2 POINTS for setting up an inequality for $n$.
This simplifies to $n^{2}<3999$, that is, $n \leq 63$. Now we check integers from $n=64$ on:
$$
\begin{aligned}
& \text { for } n=64,\left\lfloor\frac{1999}{65}\right\rfloor \cdot 63+64=30 \cdot 63+64=1954<2000 ; \\
& \text { for } n=65,\left\lfloor\frac{1999}{66}\right\rfloor \cdot 64+65=30 \cdot 64+65=1985<2000 ; \\
& \text { for } n=66,\left\lfloor\frac{1999}{67}\right\rfloor \cdot 65+66=29 \cdot 65+66=1951<2000 ; \\
& \text { for } n=67,\left\lfloor\left\lfloor\frac{1999}{68}\right\rfloor \cdot 66+67=29 \cdot 66+67=1981<2000 ;\right. \\
& \text { for } n=68,\left\lfloor\frac{1999}{69}\right\rfloor \cdot 67+68=28 \cdot 67+68=1944<2000 ; \\
& \text { for } n=69,\left\lfloor\frac{1999}{70}\right\rfloor \cdot 68+69=28 \cdot 68+69=1973<2000 ; \\
& \text { for } n=70,\left\lfloor\frac{1999}{71}\right\rfloor \cdot 69+70=28 \cdot 69+70=2002 \geq 2000 .
\end{aligned}
$$
Thus the answer is $n=70$.
1.POINT for checking these rumbers and finding that $n=70$.
|
70
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the smallest positive integer $n$ with the following property : There does not exist an arithmetic progression of 1993 terms of real numbers containing exactly $n$ integers.
|
and Marking Scheme:
We first note that the integer terms of any arithmetic progression are "equally spaced", because if the $i$ th term $a_{i}$ and the $(i+j)$ th term $a_{i+j}$ of an arithmetic progression are both integers, then so is the $(i+2 j)$ th term $a_{i+2 j}=a_{i+j}+\left(a_{i+j}-a_{i}\right)$.
1 POINT for realizing that the integers must be "equally spaced".
Thus, by scaling and translation, we can assume that the integer terms of the arithmetic progression are $1,2, \cdots, n$ and we need only to consider arithmetic progression of the form
$$
1,1+\frac{1}{k}, 1+\frac{2}{k}, \cdots, 1+\frac{k-1}{k}, 2,2+\frac{1}{k}, \cdots, n-1, \cdots, n-1+\frac{k-1}{k}, n
$$
This has $k n-k+1$ terms of which exactly $n$ are integers. Moreover we can add up to $k-1$ terms on either end and get another arithmetic progression without changing the number of integer terms.
2 POINTS for noticing that the maximal sequence has an equal number of terms on either side of the integers appearing in the sequence (this includes the 1 POINT above). In other words, 2 POINTS for the scaled and translated form of the progression including the $k-1$ terms on either side.
Thus there are arithmetic progressions with $n$ integers whose length is any integer lying in the interval $[k n-k+1, k n+k-1]$, where $k$ is any positive integer. Thus we want to find the smallest $n>0$ so that, if $k$ is the largest integer satisfying $k n+k-1 \leq 1998$, then $(k+1) n-(k+1)+1 \geq 2000$.
4 POINTS for clarifying the nature of the number $n$ in this way, which includes counting the terms of the maximal and minimal sequences containing $n$ integers and bounding them accordingly (this includes the 2 POINTS above).
That is, putting $k=\lfloor 1999 /(n+1)\rfloor$, we want the smallest integer $n$ so that
$$
\left\lfloor\frac{1999}{n+1}\right\rfloor(n-1)+n \geq 2000
$$
This inequality does not hold if
$$
\frac{1999}{n+1} \cdot(n-1)+n<2000
$$
2 POINTS for setting up an inequality for $n$.
This simplifies to $n^{2}<3999$, that is, $n \leq 63$. Now we check integers from $n=64$ on:
$$
\begin{aligned}
& \text { for } n=64,\left\lfloor\frac{1999}{65}\right\rfloor \cdot 63+64=30 \cdot 63+64=1954<2000 ; \\
& \text { for } n=65,\left\lfloor\frac{1999}{66}\right\rfloor \cdot 64+65=30 \cdot 64+65=1985<2000 ; \\
& \text { for } n=66,\left\lfloor\frac{1999}{67}\right\rfloor \cdot 65+66=29 \cdot 65+66=1951<2000 ; \\
& \text { for } n=67,\left\lfloor\left\lfloor\frac{1999}{68}\right\rfloor \cdot 66+67=29 \cdot 66+67=1981<2000 ;\right. \\
& \text { for } n=68,\left\lfloor\frac{1999}{69}\right\rfloor \cdot 67+68=28 \cdot 67+68=1944<2000 ; \\
& \text { for } n=69,\left\lfloor\frac{1999}{70}\right\rfloor \cdot 68+69=28 \cdot 68+69=1973<2000 ; \\
& \text { for } n=70,\left\lfloor\frac{1999}{71}\right\rfloor \cdot 69+70=28 \cdot 69+70=2002 \geq 2000 .
\end{aligned}
$$
Thus the answer is $n=70$.
1.POINT for checking these rumbers and finding that $n=70$.
|
{
"resource_path": "APMO/segmented/en-apmo1999_sol.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution "
}
|
2b064b65-5764-50a4-aaaf-18dcc2829667
| 604,646
|
Let $a_{1}, a_{2}, \cdots$ be a sequence of real numbers satisfying $a_{i+j} \leq a_{i}+a_{j}$ for all $i, j=1,2, \cdots$. Prove that
$$
a_{1}+\frac{a_{2}}{2}+\frac{a_{3}}{3}+\cdots+\frac{a_{n}}{n} \geq a_{n}
$$
for each positive integer $n$.
|
and Marking Scheme:
Letting $b_{i}=a_{i} / i,(i=1,2, \cdots)$, we prove that
$$
b_{1}+\cdots+b_{n} \geq a_{n} \quad(n=1,2, \cdots)
$$
by induction on $n$. For $n=1, b_{1}=a_{1} \geq a_{1}$, and the induction starts. Assume that
$$
b_{1}+\cdots+b_{k} \geq a_{k}
$$
for all $k=1,2, \cdots, n-1$. It suffices to prove that $b_{1}+\cdots+b_{n} \geq a_{n}$ or equivalently that
$$
\begin{aligned}
& n b_{1}+\cdots+n b_{n-1} \geq(n-1) a_{n} . \\
& 3 \text { POINTS for separating } a_{n} \text { from } b_{1}, \cdots, b_{n-1} \text {. } \\
& n b_{1}+\cdots+n b_{n-1}=(n-1) b_{1}+(n-2) b_{2}+\cdots+b_{n-1}+b_{1}+2 b_{2}+\cdots+(n-1) b_{n-1} \\
& =b_{1}+\left(b_{1}+b_{2}\right)+\cdots+\left(b_{1}+b_{2}+\cdots+b_{n-1}\right)+\left(a_{1}+a_{2}+\cdots+a_{n-1}\right) \\
& \geq 2\left(a_{1}+a_{2}+\cdots+a_{n-1}\right)=\sum_{i=1}^{n-1}\left(a_{i}+a_{n-i}\right) \geq(n-1) a_{n} .
\end{aligned}
$$
3 POINTS for the first inequaliny and 1 POINT for the rest.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a_{1}, a_{2}, \cdots$ be a sequence of real numbers satisfying $a_{i+j} \leq a_{i}+a_{j}$ for all $i, j=1,2, \cdots$. Prove that
$$
a_{1}+\frac{a_{2}}{2}+\frac{a_{3}}{3}+\cdots+\frac{a_{n}}{n} \geq a_{n}
$$
for each positive integer $n$.
|
and Marking Scheme:
Letting $b_{i}=a_{i} / i,(i=1,2, \cdots)$, we prove that
$$
b_{1}+\cdots+b_{n} \geq a_{n} \quad(n=1,2, \cdots)
$$
by induction on $n$. For $n=1, b_{1}=a_{1} \geq a_{1}$, and the induction starts. Assume that
$$
b_{1}+\cdots+b_{k} \geq a_{k}
$$
for all $k=1,2, \cdots, n-1$. It suffices to prove that $b_{1}+\cdots+b_{n} \geq a_{n}$ or equivalently that
$$
\begin{aligned}
& n b_{1}+\cdots+n b_{n-1} \geq(n-1) a_{n} . \\
& 3 \text { POINTS for separating } a_{n} \text { from } b_{1}, \cdots, b_{n-1} \text {. } \\
& n b_{1}+\cdots+n b_{n-1}=(n-1) b_{1}+(n-2) b_{2}+\cdots+b_{n-1}+b_{1}+2 b_{2}+\cdots+(n-1) b_{n-1} \\
& =b_{1}+\left(b_{1}+b_{2}\right)+\cdots+\left(b_{1}+b_{2}+\cdots+b_{n-1}\right)+\left(a_{1}+a_{2}+\cdots+a_{n-1}\right) \\
& \geq 2\left(a_{1}+a_{2}+\cdots+a_{n-1}\right)=\sum_{i=1}^{n-1}\left(a_{i}+a_{n-i}\right) \geq(n-1) a_{n} .
\end{aligned}
$$
3 POINTS for the first inequaliny and 1 POINT for the rest.
|
{
"resource_path": "APMO/segmented/en-apmo1999_sol.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "# Solution "
}
|
c5defa5c-148f-53da-87e8-0326891c55f5
| 604,662
|
Let $\Gamma_{1}$ and $\Gamma_{2}$ be two circles intersecting at $P$ and $Q$. The common tangent, closer to $P$, of $\Gamma_{1}$ and $\Gamma_{2}$ touches $\Gamma_{1}$ at $A$ and $\Gamma_{2}$ at $B$. The tangent of $\Gamma_{1}$ at $P$ meets $\Gamma_{2}$ at $C$, which is different from $P$ and the extension of $A P$ meets $B C$ at $R$. Prove that the circumcircle of triangle $P Q R$ is tangent to $B P$ and $B R$.
|
and Marking Scheme:
Let $\alpha=\angle P A B, \beta=\angle A B P$ y $\gamma=\angle Q A P$. Then, since $P C$ is tangent to $\Gamma_{1}$, we have $\angle Q P C=$ $\angle Q B C=\gamma$. Thus $A, B, R, Q$ are concyclic.
3 POINTS for proving that $A, B, R, Q$ are concyclic.
Since $A B$ is a common tangent to $\Gamma_{1}$ and $\Gamma_{2}$ then $\angle A Q P=\alpha$ and $\angle P Q B=\angle P C B=\beta$. Therefore, since $A, B, R, Q$ are concyclic, $\angle A R B=\angle A Q B=\alpha+\beta$ and $\angle B Q R=\alpha$. Thus $\angle P Q R=\angle P Q B+$ $\angle B Q R=\alpha+\beta$.
$$
2 \text { POINTS for proving that } \angle P Q R=\angle P R B=\alpha+\beta
$$
Since $\angle B P R$ is an exterior angle of triangle $A B P, \angle B P R=\alpha+\beta$. We have
$$
\angle P Q R=\angle B P R=\angle B R P
$$
1 POINT for proving $\angle B P R=\alpha+\beta$.
So circumcircle of $P Q R$ is tangent to $B P$ and $B R$.
1 POINT for concluding.
Remark. 2POINTS can be given for proving that $\angle P R B=\angle R P B$ and 1 more POINT for attempting to prove (unsuccessfully) that $\angle P R B=\angle R P B=\angle P Q R$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\Gamma_{1}$ and $\Gamma_{2}$ be two circles intersecting at $P$ and $Q$. The common tangent, closer to $P$, of $\Gamma_{1}$ and $\Gamma_{2}$ touches $\Gamma_{1}$ at $A$ and $\Gamma_{2}$ at $B$. The tangent of $\Gamma_{1}$ at $P$ meets $\Gamma_{2}$ at $C$, which is different from $P$ and the extension of $A P$ meets $B C$ at $R$. Prove that the circumcircle of triangle $P Q R$ is tangent to $B P$ and $B R$.
|
and Marking Scheme:
Let $\alpha=\angle P A B, \beta=\angle A B P$ y $\gamma=\angle Q A P$. Then, since $P C$ is tangent to $\Gamma_{1}$, we have $\angle Q P C=$ $\angle Q B C=\gamma$. Thus $A, B, R, Q$ are concyclic.
3 POINTS for proving that $A, B, R, Q$ are concyclic.
Since $A B$ is a common tangent to $\Gamma_{1}$ and $\Gamma_{2}$ then $\angle A Q P=\alpha$ and $\angle P Q B=\angle P C B=\beta$. Therefore, since $A, B, R, Q$ are concyclic, $\angle A R B=\angle A Q B=\alpha+\beta$ and $\angle B Q R=\alpha$. Thus $\angle P Q R=\angle P Q B+$ $\angle B Q R=\alpha+\beta$.
$$
2 \text { POINTS for proving that } \angle P Q R=\angle P R B=\alpha+\beta
$$
Since $\angle B P R$ is an exterior angle of triangle $A B P, \angle B P R=\alpha+\beta$. We have
$$
\angle P Q R=\angle B P R=\angle B R P
$$
1 POINT for proving $\angle B P R=\alpha+\beta$.
So circumcircle of $P Q R$ is tangent to $B P$ and $B R$.
1 POINT for concluding.
Remark. 2POINTS can be given for proving that $\angle P R B=\angle R P B$ and 1 more POINT for attempting to prove (unsuccessfully) that $\angle P R B=\angle R P B=\angle P Q R$.
|
{
"resource_path": "APMO/segmented/en-apmo1999_sol.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "# Solution "
}
|
5a5af135-15a1-5ad2-9952-8863669c59e7
| 604,674
|
Determine all pairs $(a, b)$ of integers with the property that the numbers $a^{2}+4 b$ and $b^{2}+4 a$ are both perfect squares.
|
and Marking Scheme:
Without loss of gencrality, assume that $|b| \leq|a|$. If $b=0$, then $a$ must be a perfect square. So ( $a=k^{2}, b=0$ ) for each $k \in Z$ is a solution.
Now we consider the case $b \neq 0$. Because $a^{2}+4 b$ is a perfect square, the quadratic equation
$$
x^{2}+a x-b=0
$$
has two non-zero integral roots $x_{1}, x_{2}$.
2 POINTS for noticing that this equation has integral roots.
Then $x_{1}+x_{2}=-a$ and $x_{1} x_{2}=-b$, and from this it follows that
$$
\frac{1}{\left|x_{1}\right|}+\frac{1}{\left|x_{2}\right|} \geq\left|\frac{1}{x_{1}}+\frac{1}{x_{2}}\right|=\frac{|a|}{|b|} \geq 1
$$
Hence there is at least one root, say $x_{1}$, such that $\left|x_{1}\right| \leq 2$.
3 POINTS for finding that $\left|x_{1}\right| \leq 2$.
There are the following possibilities.
(1) $x_{1}=2$. Substituting $x_{1}=2$ into ( $*$ ) we get $b=2 a+4$. So we have $b^{2}+4 a=(2 a+4)^{2}+4 a=$ $4 a^{2}+20 a+16=(2 a+5)^{2}-9$. It is casy to see that the solution in non-negative integers of the equation $x^{2}-9=y^{2}$ is $(3,0)$. Hence $2 a+5= \pm 3$. From this we obtain $a=-4, b=-4$ and $a=-1, b=2$. The latter should be rejected because of the assumption $|a| \geq|b|$.
(2) $x_{1}=-2$. Substituting $x_{1}=-2$ into (*) we get $b=4-2 a$. Hence $b^{2}+4 a=4 a^{2}-12 a+16=$ $(2 a-3)^{2}+7$. It is easy to show that the solution in non-negative integers of the equation $x^{2}+7=y^{2}$ is $(3,4)$. Hence $2 a-3= \pm 3$. From this we obtain $a=3, b=-2$.
(3) $x_{1}=1$. Substituting $x_{1}=1$ into $(*)$ we get $b=a+1$. Hence $b^{2}+4 a=a^{2}+6 a+1=(a+3)^{2}-8$. It is easy to show that the solution in non-negative integers of the equation $x^{2}-8=y^{2}$ is $(3,1)$. Hence $a+3= \pm 3$. From this we obtain $a=-6, b=-5$.
(4) $x_{1}=-1$. Substituting $x_{1}=-1$ into (*) we get $b=1-a$. Then $a^{2}+4 b=(a-2)^{2}, b^{2}+4 a=(a+1)^{2}$. Consequently, $a=k, b=1-k(k \in Z)$ is a solution.
Testing these solutions and by symmetry we obtain the following solutions
$$
(-4,-4),(-5,-6),(-6,-5),\left(0, k^{2}\right),\left(k^{2}, 0\right),(k, 1-k)
$$
where $k$ is an arbitrary integer. (Observe that the solution $(3,-2)$ obtained in the second possibility is included in the last solution as a special case.)
1 POINT for writing up the correct answer.
|
(-4,-4),(-5,-6),(-6,-5),(0, k^{2}),(k^{2}, 0),(k, 1-k)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Determine all pairs $(a, b)$ of integers with the property that the numbers $a^{2}+4 b$ and $b^{2}+4 a$ are both perfect squares.
|
and Marking Scheme:
Without loss of gencrality, assume that $|b| \leq|a|$. If $b=0$, then $a$ must be a perfect square. So ( $a=k^{2}, b=0$ ) for each $k \in Z$ is a solution.
Now we consider the case $b \neq 0$. Because $a^{2}+4 b$ is a perfect square, the quadratic equation
$$
x^{2}+a x-b=0
$$
has two non-zero integral roots $x_{1}, x_{2}$.
2 POINTS for noticing that this equation has integral roots.
Then $x_{1}+x_{2}=-a$ and $x_{1} x_{2}=-b$, and from this it follows that
$$
\frac{1}{\left|x_{1}\right|}+\frac{1}{\left|x_{2}\right|} \geq\left|\frac{1}{x_{1}}+\frac{1}{x_{2}}\right|=\frac{|a|}{|b|} \geq 1
$$
Hence there is at least one root, say $x_{1}$, such that $\left|x_{1}\right| \leq 2$.
3 POINTS for finding that $\left|x_{1}\right| \leq 2$.
There are the following possibilities.
(1) $x_{1}=2$. Substituting $x_{1}=2$ into ( $*$ ) we get $b=2 a+4$. So we have $b^{2}+4 a=(2 a+4)^{2}+4 a=$ $4 a^{2}+20 a+16=(2 a+5)^{2}-9$. It is casy to see that the solution in non-negative integers of the equation $x^{2}-9=y^{2}$ is $(3,0)$. Hence $2 a+5= \pm 3$. From this we obtain $a=-4, b=-4$ and $a=-1, b=2$. The latter should be rejected because of the assumption $|a| \geq|b|$.
(2) $x_{1}=-2$. Substituting $x_{1}=-2$ into (*) we get $b=4-2 a$. Hence $b^{2}+4 a=4 a^{2}-12 a+16=$ $(2 a-3)^{2}+7$. It is easy to show that the solution in non-negative integers of the equation $x^{2}+7=y^{2}$ is $(3,4)$. Hence $2 a-3= \pm 3$. From this we obtain $a=3, b=-2$.
(3) $x_{1}=1$. Substituting $x_{1}=1$ into $(*)$ we get $b=a+1$. Hence $b^{2}+4 a=a^{2}+6 a+1=(a+3)^{2}-8$. It is easy to show that the solution in non-negative integers of the equation $x^{2}-8=y^{2}$ is $(3,1)$. Hence $a+3= \pm 3$. From this we obtain $a=-6, b=-5$.
(4) $x_{1}=-1$. Substituting $x_{1}=-1$ into (*) we get $b=1-a$. Then $a^{2}+4 b=(a-2)^{2}, b^{2}+4 a=(a+1)^{2}$. Consequently, $a=k, b=1-k(k \in Z)$ is a solution.
Testing these solutions and by symmetry we obtain the following solutions
$$
(-4,-4),(-5,-6),(-6,-5),\left(0, k^{2}\right),\left(k^{2}, 0\right),(k, 1-k)
$$
where $k$ is an arbitrary integer. (Observe that the solution $(3,-2)$ obtained in the second possibility is included in the last solution as a special case.)
1 POINT for writing up the correct answer.
|
{
"resource_path": "APMO/segmented/en-apmo1999_sol.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "# First Solution "
}
|
7c4d4e1a-65b2-5da0-9f56-84892db721c8
| 604,688
|
Determine all pairs $(a, b)$ of integers with the property that the numbers $a^{2}+4 b$ and $b^{2}+4 a$ are both perfect squares.
|
and Marking Scheme:
Without loss of generality assume that $|b| \leq|a|$. Then $a^{2}+4 b \leq a^{2}+4|a|<a^{2}+4|a|+4=(|a|+2)^{2}$. Given that $a^{2}+4 b$ is a perfect square and since $a^{2}+4 b$ y $a^{2}$ have same parity then $a^{2}+4 b \neq(|a|+1)^{2}$, so
$$
a^{2}+4 b \leq a^{2}
$$
2 POINTS for proving (1).
Let us consider three cases.
Case 1. $a^{2}+4 b=a^{2}$. Then $b=0$ and $a$ must be a perfect square. So $a=k^{2}, b=0(k \in Z)$ is a solution.
Case 2. $a^{2}+4 b=(|a|-2)^{2}$. Then $b=1-|a|$, therefore $b^{2}+4 a=a^{2}-2|a|+4 a+1$ must be a perfect square.
If $a>0$ then $b^{2}+4 a=(a+1)^{2}$ is a perfect square for each $a \in Z$. Consequently $a=k$ and $b=1-k$ ( $k \in Z^{+}$) is a solution.
If $a=0$ then $b=1$, but from (1) $b$ must be non-positive.
If $a<0$ then $b^{2}+4 a=m^{2}-6 m+1$ must be a perfect square, where $m=-a>0$. For $m \geq 8$
$$
(m-3)^{2}>m^{2}-6 m+1>(m-4)^{2}
$$
therefore $m<8$. If $m=1,2,3,4,5$ then $m^{2}-6 m+1<0$. If $m=6, m^{2}-6 m+1=1$ is a perfect square thus $a=-6$ and $b=-5$ is a solution. If $m=7, m^{2}-6 m+1=8$ is not a perfect square.
2 POINTS for case 1 and case 2.
Case 3. $a^{2}+4 b \leq(|a|-4)^{2}$. Since $|b| \leq|a|$ then $b \geq-|a|$, thus $a^{2}-4|a| \leq a^{2}+4 b \leq(|a|-4)^{2}$. It follows that $|a| \leq 4$. We have following posibilities:
## 1 POINT for finding that $|a| \leq 4$ in this case.
(a) $|a|=4$. Then $16+4 b=0$ or $b=-4$. Thus $b^{2}+4 a=16 \pm 16$ must be a perfect square. So $a=-4$ y $b=-4$.
(b) $|a|=3$. In this case $a^{2}+4 b=9+4 b \leq 1$, then $9+4 b=0$ or $9+4 b=1$. The equation $9+4 b=0$ does not have integer solutions. The solution of the second equation is $b=-2$. Then $b^{2}+4 a=4 \pm 12$ must be a perfect square, thus $a=3$.
(c) $|a|=2 \cdot a^{2}+4 b=4+4 b \leq 4$. Since $4+4 b$ is cven and must be a perfect square then $4+4 b=4$ or $4+4 b=0$. Therefore $b=0$ or $b=-1$. If $b=0, b^{2}+4 a= \pm 8$ is not a perfect square. If $b=-1$ then $b^{2}+4 a=1 \pm 8$ is a perfect square if $a=2$. Thus $a=2$ and $b=-1$ is a solution.
(d) $|a|=1$. Then $a^{2}+4 b=4 b+1 \leq 9$. Since $4 b+1$ must be an odd perfect square then $4 b+1=1$ or $4 b+1=9$. So $b=0$ or $b=2$. If $b=0, b^{2}+4 a= \pm 4$, then $a=1$. If $b=2$ then $a=-1$, but this is not possible because $|b| \leq|a|$. Thus $a=1$ y $b=0$ is a solution in this case.
(c) $|a|=0$. Since $|b| \leq|a|$ then $b=0$.
1 POINT for concluding case 3.
Testing these solutions and by symmetry we obtain the following solutions:
$$
\left(k^{2}, 0\right),\left(0, k^{2}\right),(k, 1-k),(-6,-5),(-5,-6),(-4,-4)
$$
where $k$ is an arbitrary integer. Note that if $(k, 1-k)$ is a solution with $k>0$, then taking $t=1-k$, $k=1-t$, so $(1-t, t)$ is solution. Thus by symetry $(k, 1-k)$ is a solution for any integer.
1 POINT for writing up the correct answer.
Remark: I POINT can be given for checking that $(k, 1-k)$ is a solution. However NO POINT is given for finding any other particular solution.
|
(k^{2}, 0), (0, k^{2}), (k, 1-k), (-6, -5), (-5, -6), (-4, -4)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Determine all pairs $(a, b)$ of integers with the property that the numbers $a^{2}+4 b$ and $b^{2}+4 a$ are both perfect squares.
|
and Marking Scheme:
Without loss of generality assume that $|b| \leq|a|$. Then $a^{2}+4 b \leq a^{2}+4|a|<a^{2}+4|a|+4=(|a|+2)^{2}$. Given that $a^{2}+4 b$ is a perfect square and since $a^{2}+4 b$ y $a^{2}$ have same parity then $a^{2}+4 b \neq(|a|+1)^{2}$, so
$$
a^{2}+4 b \leq a^{2}
$$
2 POINTS for proving (1).
Let us consider three cases.
Case 1. $a^{2}+4 b=a^{2}$. Then $b=0$ and $a$ must be a perfect square. So $a=k^{2}, b=0(k \in Z)$ is a solution.
Case 2. $a^{2}+4 b=(|a|-2)^{2}$. Then $b=1-|a|$, therefore $b^{2}+4 a=a^{2}-2|a|+4 a+1$ must be a perfect square.
If $a>0$ then $b^{2}+4 a=(a+1)^{2}$ is a perfect square for each $a \in Z$. Consequently $a=k$ and $b=1-k$ ( $k \in Z^{+}$) is a solution.
If $a=0$ then $b=1$, but from (1) $b$ must be non-positive.
If $a<0$ then $b^{2}+4 a=m^{2}-6 m+1$ must be a perfect square, where $m=-a>0$. For $m \geq 8$
$$
(m-3)^{2}>m^{2}-6 m+1>(m-4)^{2}
$$
therefore $m<8$. If $m=1,2,3,4,5$ then $m^{2}-6 m+1<0$. If $m=6, m^{2}-6 m+1=1$ is a perfect square thus $a=-6$ and $b=-5$ is a solution. If $m=7, m^{2}-6 m+1=8$ is not a perfect square.
2 POINTS for case 1 and case 2.
Case 3. $a^{2}+4 b \leq(|a|-4)^{2}$. Since $|b| \leq|a|$ then $b \geq-|a|$, thus $a^{2}-4|a| \leq a^{2}+4 b \leq(|a|-4)^{2}$. It follows that $|a| \leq 4$. We have following posibilities:
## 1 POINT for finding that $|a| \leq 4$ in this case.
(a) $|a|=4$. Then $16+4 b=0$ or $b=-4$. Thus $b^{2}+4 a=16 \pm 16$ must be a perfect square. So $a=-4$ y $b=-4$.
(b) $|a|=3$. In this case $a^{2}+4 b=9+4 b \leq 1$, then $9+4 b=0$ or $9+4 b=1$. The equation $9+4 b=0$ does not have integer solutions. The solution of the second equation is $b=-2$. Then $b^{2}+4 a=4 \pm 12$ must be a perfect square, thus $a=3$.
(c) $|a|=2 \cdot a^{2}+4 b=4+4 b \leq 4$. Since $4+4 b$ is cven and must be a perfect square then $4+4 b=4$ or $4+4 b=0$. Therefore $b=0$ or $b=-1$. If $b=0, b^{2}+4 a= \pm 8$ is not a perfect square. If $b=-1$ then $b^{2}+4 a=1 \pm 8$ is a perfect square if $a=2$. Thus $a=2$ and $b=-1$ is a solution.
(d) $|a|=1$. Then $a^{2}+4 b=4 b+1 \leq 9$. Since $4 b+1$ must be an odd perfect square then $4 b+1=1$ or $4 b+1=9$. So $b=0$ or $b=2$. If $b=0, b^{2}+4 a= \pm 4$, then $a=1$. If $b=2$ then $a=-1$, but this is not possible because $|b| \leq|a|$. Thus $a=1$ y $b=0$ is a solution in this case.
(c) $|a|=0$. Since $|b| \leq|a|$ then $b=0$.
1 POINT for concluding case 3.
Testing these solutions and by symmetry we obtain the following solutions:
$$
\left(k^{2}, 0\right),\left(0, k^{2}\right),(k, 1-k),(-6,-5),(-5,-6),(-4,-4)
$$
where $k$ is an arbitrary integer. Note that if $(k, 1-k)$ is a solution with $k>0$, then taking $t=1-k$, $k=1-t$, so $(1-t, t)$ is solution. Thus by symetry $(k, 1-k)$ is a solution for any integer.
1 POINT for writing up the correct answer.
Remark: I POINT can be given for checking that $(k, 1-k)$ is a solution. However NO POINT is given for finding any other particular solution.
|
{
"resource_path": "APMO/segmented/en-apmo1999_sol.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "# Second Solution "
}
|
7c4d4e1a-65b2-5da0-9f56-84892db721c8
| 604,688
|
Let $S$ be a set of $2 n+1$ points in the plane such that no three are collinear and no four concyclic. A circle will be called good if it has 3 points of $S$ on its circumference, $n-1$ points in its interior and $n-1$ in its exterior. Prove that the number of good circles has the same parity as $n$.
|
and Marking Scheme:
Lemma 1. Let $P$ and $Q$ be two points of $S$. The number of good circles that contain $P$ and $Q$ on their circumference is odd.
## Proof of Lemma 1.
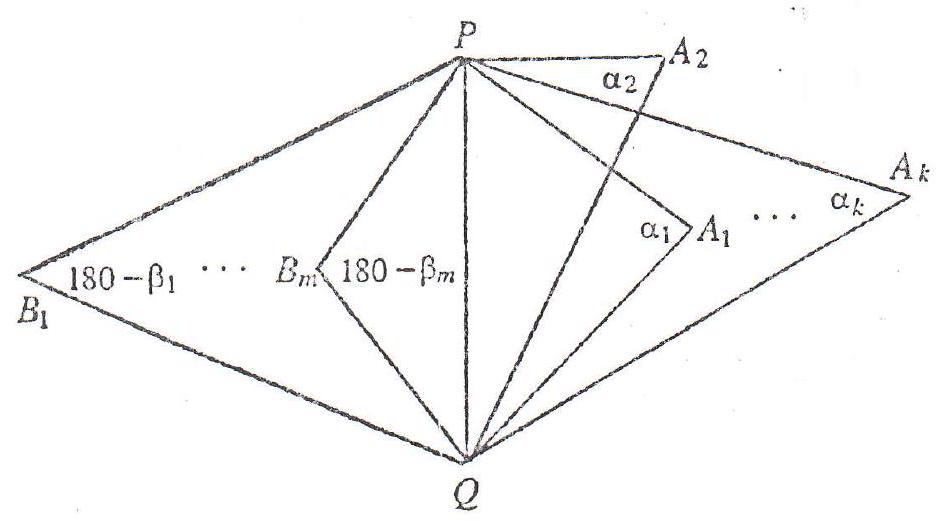
Let $N$ be the number of good circles that pass through $P$ and $Q$. Number the points on one side of the line $P Q$ by $A_{1}, A_{2}, \ldots, A_{k}$ and those on the other side by $B_{1}, B_{2}, \ldots, B_{m}$ in such a way that if $\angle P A_{i} Q=\alpha_{i}, \angle P B_{j} Q=180-\beta_{j}$ then $\alpha_{1}>\alpha_{2}>\ldots>\alpha_{k}$ and $\beta_{1}>\beta_{2}>\ldots>\beta_{m}$.
Note that the angles $\alpha_{1}, \alpha_{2}, \ldots, \alpha_{k}, \beta_{1}, \beta_{2}, \ldots, \beta_{m}$ are all distinct since there are no four points in $S$ that are concyclic.
Observe that the circle that passes through $P, Q$ and $A_{i}$ has $A_{j}$ in its interior when $\alpha_{j}>\alpha_{i}$ that is, when $i>j$; and it contains $B_{j}$ in its interior when $\alpha_{i}+180-\beta_{j}>180$, that is, when $\alpha_{i}>\beta_{j}$. Similar conditions apply to the circle that contains $P, Q$ and $B_{j}$.
1 POINT for characterizing the points that lie inside a given circle ins terms of these angles, or for similar considerations.
Order the angles $\alpha_{1}, \alpha_{2}, \ldots, \alpha_{k}, \beta_{1}, \beta_{2}, \ldots, \beta_{m}$ from the greatest to least. Now transform $S$ as follows. Consider a $\beta_{j}$ that bas an $\alpha_{i}$ immediately to its left in such an ordering ( $\ldots>\alpha_{i}>\beta_{j} \ldots$ ). Consider a new set $S^{\prime}$ that contains the same points as $S$ except for $A_{i}$ and $B_{j}$. These two points will be replaced by $A_{i}^{\prime}$ and $B_{j}^{\prime}$ that satisfy $\angle P A_{i}^{\prime} Q=\beta_{j}=\alpha_{i}^{\prime}$ and $\angle P B_{j}^{\prime} Q=180-\alpha_{i}^{\prime \prime}=180-\beta_{j}^{\prime}$. Thus $\beta_{j}$ and $\alpha_{i}$ have been interchanged and the ordering of the $\alpha$ 's and $\beta$ 's has only changed with respect to the relative order of $\alpha_{i}$ and $\beta_{j}$; we continue to have
$$
\alpha_{1}>\alpha_{2}>\ldots>\alpha_{i-1}>\alpha_{i}^{\prime}>\alpha_{i+1}>\ldots>\alpha_{k}
$$
and
$$
\beta_{1}>\beta_{2}>\ldots>\beta_{j-1}>\beta_{j}^{\prime}>\beta_{j+1}>\ldots>\beta_{m}
$$
1 POINT for this or another useful transformation of the set $S$.
Analyze the good circles in this new set $S^{\prime}$. Clearly, a circle through $P, Q, A_{r}(r \neq i)$ or through $P, Q, B_{s}(s \neq j)$ that was good in $S$ will also be good in $S^{\prime}$, because the order of $A_{r}$ (or $B_{s}$ ) relative to the rest of the points has not changed, and therefore the number of points in the interior or exterior of this circle has not changed. The only changes that could have taken place are:
a) If the circle $P, Q, A_{i}$ was good in $S$, the circle $P, Q, A_{i}^{\prime}$ may not be good in $S^{\prime}$.
b) If the circle $P, Q, B_{j}$ was good in $S$, the circle $P, Q, B_{j}^{\prime}$ may not be good in $S^{\prime}$.
c) If the circle $P, Q, A_{i}$ was not good in $S$, the circle $P, Q, A_{i}^{\prime}$ may be good in $S^{\prime}$.
d) If the circle $P, Q, B_{j}$ was not good in $S$, the circle $P, Q, B_{j}^{\prime}$ may be good in $S^{\prime}$.
1 POINT for realizing that the transformation can only change the "goodness" of these circles. But observe that the circle $P, Q, A_{i}$ contains the points $A_{1}, A_{2}, \ldots, A_{i-1}, B_{j}, B_{j+1}, \ldots, B_{m}$ and does not contain the points $A_{i+1}, A_{i+2}, \ldots, A_{k}, B_{1}, B_{2}, \ldots, B_{j-1}$ in its interior. Then this circle is good if and only if $i+m-j=k-i+j-1$, which we rewrite as $j-i=\frac{1}{2}(m-k+1)$. On the other hand, the circle $P, Q, B_{j}$ contains the points $B_{j+1}, B_{j+2}, \ldots, B_{m}, A_{1}, A_{2}, \ldots, A_{i}$ and does not contain the points $B_{1}, B_{2}, \ldots, B_{j-1}, A_{i+1}, A_{i+2}, \ldots, A_{k}$ in its interior. Hence this circle is good if and only if $m-j+i=j-1+k-i$, which we rewrite as $j-i=\frac{1}{2}(m-k+1)$.
Therefore, the circle $P, Q, A_{i}$ is good if and only if the circle $P, Q, B_{j}$ is good. Similarly, the circle $P, Q, A_{i}^{\prime}$ is good if and only if the circle $P, Q, B_{j}^{\prime}$ is good. That is to say, transforming $S$ into $S^{\prime}$ we lose either 0 or 2 good circles of $S$ and we gain either 0 or 2 good circles in $S^{\prime}$.
1 POINT for realizing that the "goodness" of these circles is changed in pairs.
Continuing in this way, we may continue to transform $S$ until we obtain a new set $S_{0}$ such that the angles $\alpha_{1}^{\prime}, \alpha_{2}^{\prime}, \ldots, \alpha_{k}^{\prime}, \beta_{1}^{\prime}, \beta_{2}^{\prime}, \ldots, \beta_{m}^{\prime}$ satisfy
$$
\beta_{1}^{\prime}>\beta_{2}^{\prime}>\ldots>\beta_{n}^{\prime}>\alpha_{1}^{\prime}>\alpha_{2}^{\prime}>\ldots>\alpha_{k}^{\prime}
$$
and such that the number of good circles in $S_{0}$ has the same parity as $N$. We claim that $S_{0}$ has exactly one good circle. In this configuration, the circle $P, Q, A_{i}$ does not contain any $B_{j}$ and the circle $P, Q, B_{r}$ does not contain any $A_{s}$ (for all $\left.i, j\right)$, because $\alpha_{a}+\left(180-\beta_{b}\right)<180$ for all $a, b$. Hence, the only possible good circles are $P, Q, B_{m-n+1}$ (which contains the $n-1$ points $B_{m-n+2}, B_{m-n+3}, \ldots, B_{m}$ ), if $m-n+1>0$, and the circle $P, Q, A_{n}$ (which contains the $n-1$ points $A_{1}, A_{2}, \ldots, A_{n}$ ), if $n \leq k$. But, since $m+k=2 n-1$, which we rewrite as $m-n+1=n-k$, exactly one of the inequalitites $m-n+1>0$ and $n \leq k$ is satisfied. It follows that one of the points $B_{m-n+1}$ and $A_{n}$ corresponds to a good circle and the other does not. Hence, $S_{0}$ has exactly one good circle, and $N$ is odd.
1 POINT for showing that this configuration has exactly one good circle.
Now consider the $\binom{2 n+1}{2}$ pairs of points in $S$. Let $a_{2 k+1}$ be the number of pairs of points through which exactly $2 k+1$ good circles pass. Then
$$
a_{1}+a_{3}+a_{5}+\ldots=\binom{2 n+1}{2}
$$
But then the number of good circles in $S$ is
$$
\begin{aligned}
\frac{1}{3}\left(a_{1}+3 a_{3}+5 a_{5}+7 a_{7}+\ldots\right) & \equiv a_{1}+3 a_{3}+5 a_{5}+7 a_{7}+\ldots \\
& \equiv a_{1}+a_{3}+a_{5}+a_{7}+\ldots \\
& \equiv\binom{2 n+1}{2} \\
& \equiv n(2 n+1) \\
& \equiv n(\bmod 2) .
\end{aligned}
$$
Here we have taken into account that each good circle is counted 3 times in the expression $a_{1}+3 a_{3}+$ $5 a_{5}+7 a_{7}+\ldots$ The desired result follows.
2 POINTS for this computation.
## Alteraative Proof of Lemma 1.
Let, $A_{1}, A_{2}, \ldots, A_{2 n-1}$ be the $2 n-1$ given points other than $P$ and $Q$.
Invert the plane with respect to point $P$. Let $O, B_{1}, B_{2}, \ldots, B_{2 n-1}$ be the images of points $Q, A_{1}, A_{2}, \ldots, A_{2 n-1}$, respectively, under this inversion. Call point $B_{i}$ "good" if the line $O B_{i}$ splits the points $B_{1}, B_{2} \ldots, B_{i-1}, B_{i+1}, \ldots, B_{2 n-1}$ evenly, leaving $n-1$ of them to each side of it. (Notice that no other $B_{j}$ can lie on the line $O B_{i}$, or else the points $P, Q, A_{i}$ and $A_{j}$ would be concyclic.) Then it is clear that the circle through $P, Q$ and $A_{i}$ is good if and only if point $B_{i}$ is good. Therefore, it suffices to prove that the number of good points is odd.
1 POINT for inverting and realizing the equivalence between good circles and good points. Notice that the good points depend only on the relative positions of rays $O B_{1}, O B_{2}, \ldots, O B_{2 n-1}$, and not on the exact positions of points $B_{1}, B_{2}, \ldots, B_{2 n-1}$. Therefore we may assume, for simplicity, that $B_{1}, B_{2}, \ldots, B_{2 n-1}$ lie on the unit circle $\Gamma$ with center $O$.
1 POINT for this or a similar simplification.
Let $C_{1}, C_{2}, \ldots, C_{2 n-1}$ be the points diametrically opposite to $B_{1}, B_{2}, \ldots, B_{2 n-1}$ in $\Gamma$. As remarked earlier, no $C_{i}$ can coincide with one of the $B_{j}$ 's. We will call the $B_{i}$ 's "white points", and the $C_{i}$ 's "black points". We will refer to these $4 n-2$ points as the "colored points".
Now we prove that the number of good points is odd, which will complete the proof of the lemma. We proceed by induction on $n$. If $n=1$, the result is trivial. Now assume that the result is true for $n=k$, and consider $2 k+1$ white points $B_{1}, B_{2}, \ldots, B_{2 k+1}$ on the circle $\Gamma$ (no two of which are diametrically opposite), and their diametrically opposite black points $C_{1}, C_{2}, \ldots, C_{2 k+1}$. Call this configuration of points "configuration 1 ". It is clear that we must have two consecutive colored points on $\Gamma$ which have different colors, say $B_{i}$ and $C_{j}$. Now remove points $B_{i}, B_{j}, C_{i}$ and $C_{j}$ from $\Gamma$, to obtain "configuration 2 ", a configuration with $2 k-1$ points of each color.
1 POINT for this or a similar transformation of the set.
It is easy to verify the following two claims:
1. Point $B_{i}$ is good in configuration 1 if and only if point $B_{j}$ is good in configuration 1.
2. Let $k \neq i, j$. Then point $B_{k}$ is good in configuration 1 if and only if it is good in configuration 2.
It follows that, by removing points $B_{i}, B_{j}, C_{i}$ and $C_{j}$, the number of good points can either stay the same, or decreases by two. In any case, its parity remains unchanged. Since we know, by the induction hypothesis, that the number of good points in configuration 2 is odd, it follows that the number of good points in configuration 1 is also odd. This completes the proof.
## Another Approach to Lemma 1.
One can give another inductive proof of lemma. 1, which combines the ideas of the two proofs that we have given. The idea is to start as in the first proof, with the characterization of the points inside a given circle.
1 POINT
Then we transform the set $S$ by removing the points $A_{i}$ and $B_{j}$ instead of replacing then by $A_{i}^{p}$ and $B_{j}^{\prime}$.
1 POINT
It can be shown that every one of the romaining circles going through $P$ and $Q$, contained exactly one of $A_{i}$ and $B_{j}$. Therefore, the only good circles we could have gained or lost are $P, Q, A_{i}$ and $P, Q, B_{j}$.
2 POINTS
Finally, we show that either both or none of these circles were good, so the parity of the number of good circles isn't changed by this transformation.
1 POINT
Remark: 2 POINTS can be given if the result has been fully proved for a particular case with $n>1$. (If more than one particular case has been analyzed completly, only 2 POINTS.) These points are awarded only if no progress has been made in the general solution of the problem.
|
proof
|
Yes
|
Incomplete
|
proof
|
Combinatorics
|
Let $S$ be a set of $2 n+1$ points in the plane such that no three are collinear and no four concyclic. A circle will be called good if it has 3 points of $S$ on its circumference, $n-1$ points in its interior and $n-1$ in its exterior. Prove that the number of good circles has the same parity as $n$.
|
and Marking Scheme:
Lemma 1. Let $P$ and $Q$ be two points of $S$. The number of good circles that contain $P$ and $Q$ on their circumference is odd.
## Proof of Lemma 1.

Let $N$ be the number of good circles that pass through $P$ and $Q$. Number the points on one side of the line $P Q$ by $A_{1}, A_{2}, \ldots, A_{k}$ and those on the other side by $B_{1}, B_{2}, \ldots, B_{m}$ in such a way that if $\angle P A_{i} Q=\alpha_{i}, \angle P B_{j} Q=180-\beta_{j}$ then $\alpha_{1}>\alpha_{2}>\ldots>\alpha_{k}$ and $\beta_{1}>\beta_{2}>\ldots>\beta_{m}$.
Note that the angles $\alpha_{1}, \alpha_{2}, \ldots, \alpha_{k}, \beta_{1}, \beta_{2}, \ldots, \beta_{m}$ are all distinct since there are no four points in $S$ that are concyclic.
Observe that the circle that passes through $P, Q$ and $A_{i}$ has $A_{j}$ in its interior when $\alpha_{j}>\alpha_{i}$ that is, when $i>j$; and it contains $B_{j}$ in its interior when $\alpha_{i}+180-\beta_{j}>180$, that is, when $\alpha_{i}>\beta_{j}$. Similar conditions apply to the circle that contains $P, Q$ and $B_{j}$.
1 POINT for characterizing the points that lie inside a given circle ins terms of these angles, or for similar considerations.
Order the angles $\alpha_{1}, \alpha_{2}, \ldots, \alpha_{k}, \beta_{1}, \beta_{2}, \ldots, \beta_{m}$ from the greatest to least. Now transform $S$ as follows. Consider a $\beta_{j}$ that bas an $\alpha_{i}$ immediately to its left in such an ordering ( $\ldots>\alpha_{i}>\beta_{j} \ldots$ ). Consider a new set $S^{\prime}$ that contains the same points as $S$ except for $A_{i}$ and $B_{j}$. These two points will be replaced by $A_{i}^{\prime}$ and $B_{j}^{\prime}$ that satisfy $\angle P A_{i}^{\prime} Q=\beta_{j}=\alpha_{i}^{\prime}$ and $\angle P B_{j}^{\prime} Q=180-\alpha_{i}^{\prime \prime}=180-\beta_{j}^{\prime}$. Thus $\beta_{j}$ and $\alpha_{i}$ have been interchanged and the ordering of the $\alpha$ 's and $\beta$ 's has only changed with respect to the relative order of $\alpha_{i}$ and $\beta_{j}$; we continue to have
$$
\alpha_{1}>\alpha_{2}>\ldots>\alpha_{i-1}>\alpha_{i}^{\prime}>\alpha_{i+1}>\ldots>\alpha_{k}
$$
and
$$
\beta_{1}>\beta_{2}>\ldots>\beta_{j-1}>\beta_{j}^{\prime}>\beta_{j+1}>\ldots>\beta_{m}
$$
1 POINT for this or another useful transformation of the set $S$.
Analyze the good circles in this new set $S^{\prime}$. Clearly, a circle through $P, Q, A_{r}(r \neq i)$ or through $P, Q, B_{s}(s \neq j)$ that was good in $S$ will also be good in $S^{\prime}$, because the order of $A_{r}$ (or $B_{s}$ ) relative to the rest of the points has not changed, and therefore the number of points in the interior or exterior of this circle has not changed. The only changes that could have taken place are:
a) If the circle $P, Q, A_{i}$ was good in $S$, the circle $P, Q, A_{i}^{\prime}$ may not be good in $S^{\prime}$.
b) If the circle $P, Q, B_{j}$ was good in $S$, the circle $P, Q, B_{j}^{\prime}$ may not be good in $S^{\prime}$.
c) If the circle $P, Q, A_{i}$ was not good in $S$, the circle $P, Q, A_{i}^{\prime}$ may be good in $S^{\prime}$.
d) If the circle $P, Q, B_{j}$ was not good in $S$, the circle $P, Q, B_{j}^{\prime}$ may be good in $S^{\prime}$.
1 POINT for realizing that the transformation can only change the "goodness" of these circles. But observe that the circle $P, Q, A_{i}$ contains the points $A_{1}, A_{2}, \ldots, A_{i-1}, B_{j}, B_{j+1}, \ldots, B_{m}$ and does not contain the points $A_{i+1}, A_{i+2}, \ldots, A_{k}, B_{1}, B_{2}, \ldots, B_{j-1}$ in its interior. Then this circle is good if and only if $i+m-j=k-i+j-1$, which we rewrite as $j-i=\frac{1}{2}(m-k+1)$. On the other hand, the circle $P, Q, B_{j}$ contains the points $B_{j+1}, B_{j+2}, \ldots, B_{m}, A_{1}, A_{2}, \ldots, A_{i}$ and does not contain the points $B_{1}, B_{2}, \ldots, B_{j-1}, A_{i+1}, A_{i+2}, \ldots, A_{k}$ in its interior. Hence this circle is good if and only if $m-j+i=j-1+k-i$, which we rewrite as $j-i=\frac{1}{2}(m-k+1)$.
Therefore, the circle $P, Q, A_{i}$ is good if and only if the circle $P, Q, B_{j}$ is good. Similarly, the circle $P, Q, A_{i}^{\prime}$ is good if and only if the circle $P, Q, B_{j}^{\prime}$ is good. That is to say, transforming $S$ into $S^{\prime}$ we lose either 0 or 2 good circles of $S$ and we gain either 0 or 2 good circles in $S^{\prime}$.
1 POINT for realizing that the "goodness" of these circles is changed in pairs.
Continuing in this way, we may continue to transform $S$ until we obtain a new set $S_{0}$ such that the angles $\alpha_{1}^{\prime}, \alpha_{2}^{\prime}, \ldots, \alpha_{k}^{\prime}, \beta_{1}^{\prime}, \beta_{2}^{\prime}, \ldots, \beta_{m}^{\prime}$ satisfy
$$
\beta_{1}^{\prime}>\beta_{2}^{\prime}>\ldots>\beta_{n}^{\prime}>\alpha_{1}^{\prime}>\alpha_{2}^{\prime}>\ldots>\alpha_{k}^{\prime}
$$
and such that the number of good circles in $S_{0}$ has the same parity as $N$. We claim that $S_{0}$ has exactly one good circle. In this configuration, the circle $P, Q, A_{i}$ does not contain any $B_{j}$ and the circle $P, Q, B_{r}$ does not contain any $A_{s}$ (for all $\left.i, j\right)$, because $\alpha_{a}+\left(180-\beta_{b}\right)<180$ for all $a, b$. Hence, the only possible good circles are $P, Q, B_{m-n+1}$ (which contains the $n-1$ points $B_{m-n+2}, B_{m-n+3}, \ldots, B_{m}$ ), if $m-n+1>0$, and the circle $P, Q, A_{n}$ (which contains the $n-1$ points $A_{1}, A_{2}, \ldots, A_{n}$ ), if $n \leq k$. But, since $m+k=2 n-1$, which we rewrite as $m-n+1=n-k$, exactly one of the inequalitites $m-n+1>0$ and $n \leq k$ is satisfied. It follows that one of the points $B_{m-n+1}$ and $A_{n}$ corresponds to a good circle and the other does not. Hence, $S_{0}$ has exactly one good circle, and $N$ is odd.
1 POINT for showing that this configuration has exactly one good circle.
Now consider the $\binom{2 n+1}{2}$ pairs of points in $S$. Let $a_{2 k+1}$ be the number of pairs of points through which exactly $2 k+1$ good circles pass. Then
$$
a_{1}+a_{3}+a_{5}+\ldots=\binom{2 n+1}{2}
$$
But then the number of good circles in $S$ is
$$
\begin{aligned}
\frac{1}{3}\left(a_{1}+3 a_{3}+5 a_{5}+7 a_{7}+\ldots\right) & \equiv a_{1}+3 a_{3}+5 a_{5}+7 a_{7}+\ldots \\
& \equiv a_{1}+a_{3}+a_{5}+a_{7}+\ldots \\
& \equiv\binom{2 n+1}{2} \\
& \equiv n(2 n+1) \\
& \equiv n(\bmod 2) .
\end{aligned}
$$
Here we have taken into account that each good circle is counted 3 times in the expression $a_{1}+3 a_{3}+$ $5 a_{5}+7 a_{7}+\ldots$ The desired result follows.
2 POINTS for this computation.
## Alteraative Proof of Lemma 1.
Let, $A_{1}, A_{2}, \ldots, A_{2 n-1}$ be the $2 n-1$ given points other than $P$ and $Q$.
Invert the plane with respect to point $P$. Let $O, B_{1}, B_{2}, \ldots, B_{2 n-1}$ be the images of points $Q, A_{1}, A_{2}, \ldots, A_{2 n-1}$, respectively, under this inversion. Call point $B_{i}$ "good" if the line $O B_{i}$ splits the points $B_{1}, B_{2} \ldots, B_{i-1}, B_{i+1}, \ldots, B_{2 n-1}$ evenly, leaving $n-1$ of them to each side of it. (Notice that no other $B_{j}$ can lie on the line $O B_{i}$, or else the points $P, Q, A_{i}$ and $A_{j}$ would be concyclic.) Then it is clear that the circle through $P, Q$ and $A_{i}$ is good if and only if point $B_{i}$ is good. Therefore, it suffices to prove that the number of good points is odd.
1 POINT for inverting and realizing the equivalence between good circles and good points. Notice that the good points depend only on the relative positions of rays $O B_{1}, O B_{2}, \ldots, O B_{2 n-1}$, and not on the exact positions of points $B_{1}, B_{2}, \ldots, B_{2 n-1}$. Therefore we may assume, for simplicity, that $B_{1}, B_{2}, \ldots, B_{2 n-1}$ lie on the unit circle $\Gamma$ with center $O$.
1 POINT for this or a similar simplification.
Let $C_{1}, C_{2}, \ldots, C_{2 n-1}$ be the points diametrically opposite to $B_{1}, B_{2}, \ldots, B_{2 n-1}$ in $\Gamma$. As remarked earlier, no $C_{i}$ can coincide with one of the $B_{j}$ 's. We will call the $B_{i}$ 's "white points", and the $C_{i}$ 's "black points". We will refer to these $4 n-2$ points as the "colored points".
Now we prove that the number of good points is odd, which will complete the proof of the lemma. We proceed by induction on $n$. If $n=1$, the result is trivial. Now assume that the result is true for $n=k$, and consider $2 k+1$ white points $B_{1}, B_{2}, \ldots, B_{2 k+1}$ on the circle $\Gamma$ (no two of which are diametrically opposite), and their diametrically opposite black points $C_{1}, C_{2}, \ldots, C_{2 k+1}$. Call this configuration of points "configuration 1 ". It is clear that we must have two consecutive colored points on $\Gamma$ which have different colors, say $B_{i}$ and $C_{j}$. Now remove points $B_{i}, B_{j}, C_{i}$ and $C_{j}$ from $\Gamma$, to obtain "configuration 2 ", a configuration with $2 k-1$ points of each color.
1 POINT for this or a similar transformation of the set.
It is easy to verify the following two claims:
1. Point $B_{i}$ is good in configuration 1 if and only if point $B_{j}$ is good in configuration 1.
2. Let $k \neq i, j$. Then point $B_{k}$ is good in configuration 1 if and only if it is good in configuration 2.
It follows that, by removing points $B_{i}, B_{j}, C_{i}$ and $C_{j}$, the number of good points can either stay the same, or decreases by two. In any case, its parity remains unchanged. Since we know, by the induction hypothesis, that the number of good points in configuration 2 is odd, it follows that the number of good points in configuration 1 is also odd. This completes the proof.
## Another Approach to Lemma 1.
One can give another inductive proof of lemma. 1, which combines the ideas of the two proofs that we have given. The idea is to start as in the first proof, with the characterization of the points inside a given circle.
1 POINT
Then we transform the set $S$ by removing the points $A_{i}$ and $B_{j}$ instead of replacing then by $A_{i}^{p}$ and $B_{j}^{\prime}$.
1 POINT
It can be shown that every one of the romaining circles going through $P$ and $Q$, contained exactly one of $A_{i}$ and $B_{j}$. Therefore, the only good circles we could have gained or lost are $P, Q, A_{i}$ and $P, Q, B_{j}$.
2 POINTS
Finally, we show that either both or none of these circles were good, so the parity of the number of good circles isn't changed by this transformation.
1 POINT
Remark: 2 POINTS can be given if the result has been fully proved for a particular case with $n>1$. (If more than one particular case has been analyzed completly, only 2 POINTS.) These points are awarded only if no progress has been made in the general solution of the problem.
|
{
"resource_path": "APMO/segmented/en-apmo1999_sol.jsonl",
"problem_match": "\nProblem 5.",
"solution_match": "# Solution "
}
|
83ce1daf-92ca-538a-afb1-d7c81e156798
| 604,713
|
Compute the sum $S=\sum_{i=0}^{101} \frac{x_{i}^{3}}{1-3 x_{i}+3 x_{i}^{2}}$ for $x_{i}=\frac{i}{101}$.
Answer: $S=51$.
|
Since $x_{101-i}=\frac{101-i}{101}=1-\frac{i}{101}=1-x_{i}$ and
$$
1-3 x_{i}+3 x_{i}^{2}=\left(1-3 x_{i}+3 x_{i}^{2}-x_{i}^{3}\right)+x_{i}^{3}=\left(1-x_{i}\right)^{3}+x_{i}^{3}=x_{101-i}^{3}+x_{i}^{3},
$$
we have, by replacing $i$ by $101-i$ in the second sum,
$$
2 S=S+S=\sum_{i=0}^{101} \frac{x_{i}^{3}}{x_{101-i}^{3}+x_{i}^{3}}+\sum_{i=0}^{101} \frac{x_{101-i}^{3}}{x_{i}^{3}+x_{101-i}^{3}}=\sum_{i=0}^{101} \frac{x_{i}^{3}+x_{101-i}^{3}}{x_{101-i}^{3}+x_{i}^{3}}=102,
$$
so $S=51$.
|
51
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Compute the sum $S=\sum_{i=0}^{101} \frac{x_{i}^{3}}{1-3 x_{i}+3 x_{i}^{2}}$ for $x_{i}=\frac{i}{101}$.
Answer: $S=51$.
|
Since $x_{101-i}=\frac{101-i}{101}=1-\frac{i}{101}=1-x_{i}$ and
$$
1-3 x_{i}+3 x_{i}^{2}=\left(1-3 x_{i}+3 x_{i}^{2}-x_{i}^{3}\right)+x_{i}^{3}=\left(1-x_{i}\right)^{3}+x_{i}^{3}=x_{101-i}^{3}+x_{i}^{3},
$$
we have, by replacing $i$ by $101-i$ in the second sum,
$$
2 S=S+S=\sum_{i=0}^{101} \frac{x_{i}^{3}}{x_{101-i}^{3}+x_{i}^{3}}+\sum_{i=0}^{101} \frac{x_{101-i}^{3}}{x_{i}^{3}+x_{101-i}^{3}}=\sum_{i=0}^{101} \frac{x_{i}^{3}+x_{101-i}^{3}}{x_{101-i}^{3}+x_{i}^{3}}=102,
$$
so $S=51$.
|
{
"resource_path": "APMO/segmented/en-apmo2000_sol.jsonl",
"problem_match": "# Problem 1",
"solution_match": "# Solution\n\n"
}
|
9b4fe559-cb6b-5f2d-b86c-bacaacc657cb
| 604,724
|
Given the following arrangement of circles:
Each of the numbers $1,2, \ldots, 9$ is to be written into one of these circles, so that each circle contains exactly one of these numbers and
(i) the sums of the four numbers on each side of the triangle are equal;
(ii) the sums of squares of the four numbers on each side of the triangle are equal.
Find all ways in which this can be done.
Answer: The only solutions are
and the ones generated by permuting the vertices, adjusting sides and exchanging the two middle numbers on each side.
|
Let $a, b$, and $c$ be the numbers in the vertices of the triangular arrangement. Let $s$ be the sum of the numbers on each side and $t$ be the sum of the squares of the numbers on each side. Summing the numbers (or their squares) on the three sides repeats each once the numbers on the vertices (or their squares):
$$
\begin{gathered}
3 s=a+b+c+(1+2+\cdots+9)=a+b+c+45 \\
3 t=a^{2}+b^{2}+c^{2}+\left(1^{2}+2^{2}+\cdots+9^{2}\right)=a^{2}+b^{2}+c^{2}+285
\end{gathered}
$$
At any rate, $a+b+c$ and $a^{2}+b^{2}+c^{2}$ are both multiples of 3 . Since $x^{2} \equiv 0,1(\bmod 3)$, either $a, b, c$ are all multiples of 3 or none is a multiple of 3 . If two of them are $1,2 \bmod 3$ then $a+b+c \equiv 0(\bmod 3)$ implies that the other should be a multiple of 3 , which is not possible. Thus $a, b, c$ are all congruent modulo 3 , that is,
$$
\{a, b, c\}=\{3,6,9\}, \quad\{1,4,7\}, \quad \text { or } \quad\{2,5,8\}
$$
Case 1: $\{a, b, c\}=\{3,6,9\}$. Then $3 t=3^{2}+6^{2}+9^{2}+285 \Longleftrightarrow t=137$.
In this case $x^{2}+y^{2}+3^{2}+9^{2}=137 \Longleftrightarrow x^{2}+y^{2}=47$. However, 47 cannot be written as the sum of two squares. One can check manually, or realize that $47 \equiv 3(\bmod 4)$, and since $x^{2}, y^{2} \equiv 0,1(\bmod 4), x^{2}+y^{2} \equiv 0,1,2(\bmod 4)$ cannot be 47.
Hence there are no solutions in this case.
Case 2: $\{a, b, c\}=\{1,4,7\}$. Then $3 t=1^{2}+4^{2}+7^{2}+285 \Longleftrightarrow t=117$.
In this case $x^{2}+y^{2}+1^{2}+7^{2}=117 \Longleftrightarrow x^{2}+y^{2}=67 \equiv 3(\bmod 4)$, and as in the previous case there are no solutions.
Case 3: $\{a, b, c\}=\{2,5,8\}$. Then $3 t=2^{2}+5^{2}+8^{2}+285 \Longleftrightarrow t=126$.
Then
$$
\left\{\begin{array} { c }
{ x ^ { 2 } + y ^ { 2 } + 2 ^ { 2 } + 8 ^ { 2 } = 1 2 6 } \\
{ t ^ { 2 } + u ^ { 2 } + 2 ^ { 2 } + 5 ^ { 2 } = 1 2 6 } \\
{ m ^ { 2 } + n ^ { 2 } + 5 ^ { 2 } + 8 ^ { 2 } = 1 2 6 }
\end{array} \Longleftrightarrow \left\{\begin{array}{c}
x^{2}+y^{2}=58 \\
t^{2}+u^{2}=97 \\
m^{2}+n^{2}=37
\end{array}\right.\right.
$$
The only solutions to $t^{2}+u^{2}=97$ and $m^{2}+n^{2}=37$ are $\{t, u\}=\{4,9\}$ and $\{m, n\}=\{1,6\}$, respectively (again, one can check manually.) Then $\{x, y\}=\{3,7\}$, and the solutions are
and the ones generated by permuting the vertices, adjusting sides and exchanging the two middle numbers on each side. There are $3!\cdot 2^{3}=48$ such solutions.
|
48
|
Incomplete
|
Yes
|
math-word-problem
|
Combinatorics
|
Given the following arrangement of circles:

Each of the numbers $1,2, \ldots, 9$ is to be written into one of these circles, so that each circle contains exactly one of these numbers and
(i) the sums of the four numbers on each side of the triangle are equal;
(ii) the sums of squares of the four numbers on each side of the triangle are equal.
Find all ways in which this can be done.
Answer: The only solutions are

and the ones generated by permuting the vertices, adjusting sides and exchanging the two middle numbers on each side.
|
Let $a, b$, and $c$ be the numbers in the vertices of the triangular arrangement. Let $s$ be the sum of the numbers on each side and $t$ be the sum of the squares of the numbers on each side. Summing the numbers (or their squares) on the three sides repeats each once the numbers on the vertices (or their squares):
$$
\begin{gathered}
3 s=a+b+c+(1+2+\cdots+9)=a+b+c+45 \\
3 t=a^{2}+b^{2}+c^{2}+\left(1^{2}+2^{2}+\cdots+9^{2}\right)=a^{2}+b^{2}+c^{2}+285
\end{gathered}
$$
At any rate, $a+b+c$ and $a^{2}+b^{2}+c^{2}$ are both multiples of 3 . Since $x^{2} \equiv 0,1(\bmod 3)$, either $a, b, c$ are all multiples of 3 or none is a multiple of 3 . If two of them are $1,2 \bmod 3$ then $a+b+c \equiv 0(\bmod 3)$ implies that the other should be a multiple of 3 , which is not possible. Thus $a, b, c$ are all congruent modulo 3 , that is,
$$
\{a, b, c\}=\{3,6,9\}, \quad\{1,4,7\}, \quad \text { or } \quad\{2,5,8\}
$$
Case 1: $\{a, b, c\}=\{3,6,9\}$. Then $3 t=3^{2}+6^{2}+9^{2}+285 \Longleftrightarrow t=137$.

In this case $x^{2}+y^{2}+3^{2}+9^{2}=137 \Longleftrightarrow x^{2}+y^{2}=47$. However, 47 cannot be written as the sum of two squares. One can check manually, or realize that $47 \equiv 3(\bmod 4)$, and since $x^{2}, y^{2} \equiv 0,1(\bmod 4), x^{2}+y^{2} \equiv 0,1,2(\bmod 4)$ cannot be 47.
Hence there are no solutions in this case.
Case 2: $\{a, b, c\}=\{1,4,7\}$. Then $3 t=1^{2}+4^{2}+7^{2}+285 \Longleftrightarrow t=117$.

In this case $x^{2}+y^{2}+1^{2}+7^{2}=117 \Longleftrightarrow x^{2}+y^{2}=67 \equiv 3(\bmod 4)$, and as in the previous case there are no solutions.
Case 3: $\{a, b, c\}=\{2,5,8\}$. Then $3 t=2^{2}+5^{2}+8^{2}+285 \Longleftrightarrow t=126$.

Then
$$
\left\{\begin{array} { c }
{ x ^ { 2 } + y ^ { 2 } + 2 ^ { 2 } + 8 ^ { 2 } = 1 2 6 } \\
{ t ^ { 2 } + u ^ { 2 } + 2 ^ { 2 } + 5 ^ { 2 } = 1 2 6 } \\
{ m ^ { 2 } + n ^ { 2 } + 5 ^ { 2 } + 8 ^ { 2 } = 1 2 6 }
\end{array} \Longleftrightarrow \left\{\begin{array}{c}
x^{2}+y^{2}=58 \\
t^{2}+u^{2}=97 \\
m^{2}+n^{2}=37
\end{array}\right.\right.
$$
The only solutions to $t^{2}+u^{2}=97$ and $m^{2}+n^{2}=37$ are $\{t, u\}=\{4,9\}$ and $\{m, n\}=\{1,6\}$, respectively (again, one can check manually.) Then $\{x, y\}=\{3,7\}$, and the solutions are

and the ones generated by permuting the vertices, adjusting sides and exchanging the two middle numbers on each side. There are $3!\cdot 2^{3}=48$ such solutions.
|
{
"resource_path": "APMO/segmented/en-apmo2000_sol.jsonl",
"problem_match": "# Problem 2",
"solution_match": "# Solution\n\n"
}
|
1391f7f1-73e3-52d7-a1ca-b21c12531313
| 604,739
|
Let $A B C$ be a triangle. Let $M$ and $N$ be the points in which the median and angle bisector, respectively, at $A$ meet the side $B C$. Let $Q$ and $P$ be the points in which the perpendicular at $N$ to $N A$ meets $M A$ and $B A$, respectively, and $O$ be the point in which the perpendicular at $P$ to $B A$ meets $A N$ produced. Prove that $Q O$ is perpendicular to $B C$.
|
Let $A N$ meet the circumcircle of $A B C$ at point $K$, the midpoint of arc $B C$ that does not contain $A$.
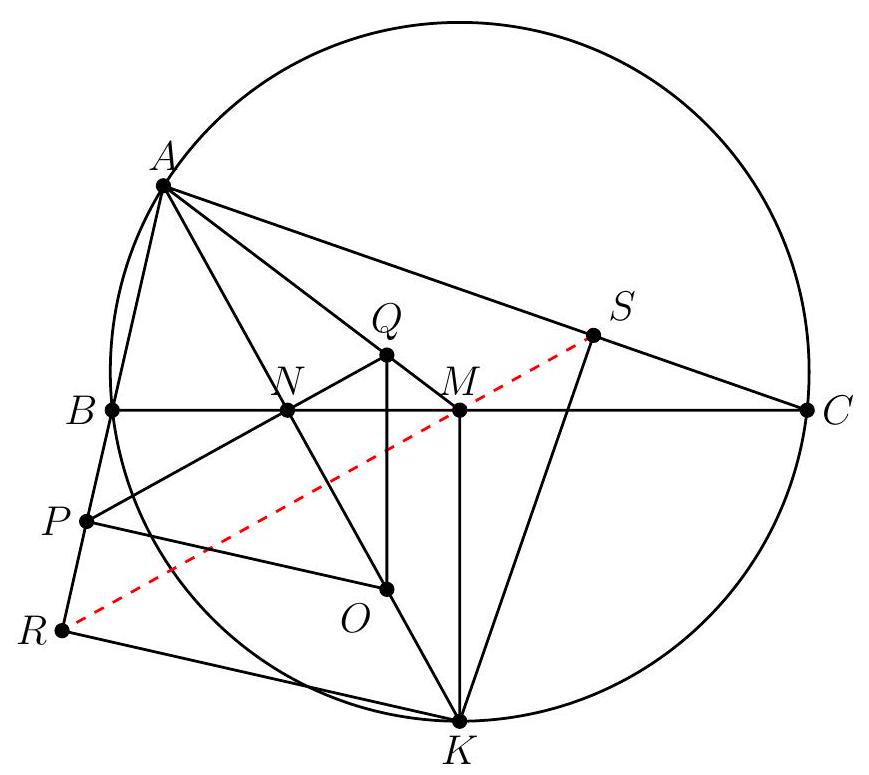
The orthogonal projection of $K$ onto side $B C$ is $M$. Let $R$ and $S$ be the orthogonal projections of $K$ onto lines $A B$ and $A C$, respectively. Points $R, M$, and $S$ lie in the Simson line of $K$ with respect to $A B C$. Since $K$ is in the bisector of $\angle B A C, A R K S$ is a kite, and the Simson line $R M S$ is perpendicular to $A N$, and therefore parallel to $P Q$.
Now consider the homothety with center $A$ that takes $O$ to $K$. Since $O P \perp A B$ and $K R \perp A B$, $O P$ and $K R$ are parallel, which means that $P$ is taken to $R$. Finally, line $P Q$ is parallel to line $R S$, so line $P Q$ is taken to line $R S$ by the homothety. Then $Q$ is taken to $M$, and since $O$ is taken to $K$, line $O Q$ is taken to line $M K$. We are done now: this means that $O Q$ is parallel to $M K$, which is perpendicular to $B C$ (it is its perpendicular bisector, as $M B=M C$ and $K B=K C$.)
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle. Let $M$ and $N$ be the points in which the median and angle bisector, respectively, at $A$ meet the side $B C$. Let $Q$ and $P$ be the points in which the perpendicular at $N$ to $N A$ meets $M A$ and $B A$, respectively, and $O$ be the point in which the perpendicular at $P$ to $B A$ meets $A N$ produced. Prove that $Q O$ is perpendicular to $B C$.
|
Let $A N$ meet the circumcircle of $A B C$ at point $K$, the midpoint of arc $B C$ that does not contain $A$.

The orthogonal projection of $K$ onto side $B C$ is $M$. Let $R$ and $S$ be the orthogonal projections of $K$ onto lines $A B$ and $A C$, respectively. Points $R, M$, and $S$ lie in the Simson line of $K$ with respect to $A B C$. Since $K$ is in the bisector of $\angle B A C, A R K S$ is a kite, and the Simson line $R M S$ is perpendicular to $A N$, and therefore parallel to $P Q$.
Now consider the homothety with center $A$ that takes $O$ to $K$. Since $O P \perp A B$ and $K R \perp A B$, $O P$ and $K R$ are parallel, which means that $P$ is taken to $R$. Finally, line $P Q$ is parallel to line $R S$, so line $P Q$ is taken to line $R S$ by the homothety. Then $Q$ is taken to $M$, and since $O$ is taken to $K$, line $O Q$ is taken to line $M K$. We are done now: this means that $O Q$ is parallel to $M K$, which is perpendicular to $B C$ (it is its perpendicular bisector, as $M B=M C$ and $K B=K C$.)
|
{
"resource_path": "APMO/segmented/en-apmo2000_sol.jsonl",
"problem_match": "# Problem 3",
"solution_match": "# Solution 1"
}
|
8fe249f3-03d2-50eb-80d7-503be84cddfd
| 295,099
|
Let $A B C$ be a triangle. Let $M$ and $N$ be the points in which the median and angle bisector, respectively, at $A$ meet the side $B C$. Let $Q$ and $P$ be the points in which the perpendicular at $N$ to $N A$ meets $M A$ and $B A$, respectively, and $O$ be the point in which the perpendicular at $P$ to $B A$ meets $A N$ produced. Prove that $Q O$ is perpendicular to $B C$.
|
Consider a cartesian plane with $A=(0,0)$ as the origin and the bisector $A N$ as $x$-axis. Thus $A B$ has equation $y=m x$ and $A C$ has equation $y=-m x$. Let $B=(b, m b)$ and $C=(c,-m c)$. By symmetry, the problem is immediate if $A B=A C$, that is, if $b=c$. Suppose that $b \neq c$ from now on. Line $B C$ has slope $\frac{m b-(-m c)}{b-c}=\frac{m(b+c)}{b-c}$. Let $N=(n, 0)$.
Point $M$ is the midpoint $\left(\frac{b+c}{2}, \frac{m b-m c}{2}\right)$ of $B C$, so $A M$ has slope $\frac{m(b-c)}{b+c}$.
The line through $N$ that is perpendicular to the $x$-axis $A N$ is $x=n$. Therefore
$$
P=(n, m n) \quad \text { and } \quad Q=\left(n, \frac{m(b-c) n}{b+c}\right) .
$$
In the right triangle $A P O$, with altitude $A N, A N \cdot A O=A P^{2}$. Thus
$$
n \cdot A O=(0-n)^{2}+(0-m n)^{2} \Longleftrightarrow A O=n\left(m^{2}+1\right) \Longrightarrow O=\left(n\left(m^{2}+1\right), 0\right)
$$
Finally, the slope of $O Q$ is
$$
\frac{\frac{m(b-c) n}{b+c}-0}{n-n\left(m^{2}+1\right)}=-\frac{b-c}{(b+c) m}
$$
Since the product of the slopes of $O Q$ and $B C$ is
$$
-\frac{b-c}{(b+c) m} \cdot \frac{m(b+c)}{b-c}=-1
$$
$O Q$ and $B C$ are perpendicular, and we are done.
Comment: The second solution shows that $N$ can be any point in the bisector of $\angle A$. In fact, if we move $N$ in the bisector and construct $O, P$ and $Q$ accordingly, then all lines $O Q$ obtained are parallel: just consider a homothety with center $A$ and variable ratios.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle. Let $M$ and $N$ be the points in which the median and angle bisector, respectively, at $A$ meet the side $B C$. Let $Q$ and $P$ be the points in which the perpendicular at $N$ to $N A$ meets $M A$ and $B A$, respectively, and $O$ be the point in which the perpendicular at $P$ to $B A$ meets $A N$ produced. Prove that $Q O$ is perpendicular to $B C$.
|
Consider a cartesian plane with $A=(0,0)$ as the origin and the bisector $A N$ as $x$-axis. Thus $A B$ has equation $y=m x$ and $A C$ has equation $y=-m x$. Let $B=(b, m b)$ and $C=(c,-m c)$. By symmetry, the problem is immediate if $A B=A C$, that is, if $b=c$. Suppose that $b \neq c$ from now on. Line $B C$ has slope $\frac{m b-(-m c)}{b-c}=\frac{m(b+c)}{b-c}$. Let $N=(n, 0)$.
Point $M$ is the midpoint $\left(\frac{b+c}{2}, \frac{m b-m c}{2}\right)$ of $B C$, so $A M$ has slope $\frac{m(b-c)}{b+c}$.
The line through $N$ that is perpendicular to the $x$-axis $A N$ is $x=n$. Therefore
$$
P=(n, m n) \quad \text { and } \quad Q=\left(n, \frac{m(b-c) n}{b+c}\right) .
$$
In the right triangle $A P O$, with altitude $A N, A N \cdot A O=A P^{2}$. Thus
$$
n \cdot A O=(0-n)^{2}+(0-m n)^{2} \Longleftrightarrow A O=n\left(m^{2}+1\right) \Longrightarrow O=\left(n\left(m^{2}+1\right), 0\right)
$$
Finally, the slope of $O Q$ is
$$
\frac{\frac{m(b-c) n}{b+c}-0}{n-n\left(m^{2}+1\right)}=-\frac{b-c}{(b+c) m}
$$
Since the product of the slopes of $O Q$ and $B C$ is
$$
-\frac{b-c}{(b+c) m} \cdot \frac{m(b+c)}{b-c}=-1
$$
$O Q$ and $B C$ are perpendicular, and we are done.
Comment: The second solution shows that $N$ can be any point in the bisector of $\angle A$. In fact, if we move $N$ in the bisector and construct $O, P$ and $Q$ accordingly, then all lines $O Q$ obtained are parallel: just consider a homothety with center $A$ and variable ratios.
|
{
"resource_path": "APMO/segmented/en-apmo2000_sol.jsonl",
"problem_match": "# Problem 3",
"solution_match": "# Solution 2"
}
|
8fe249f3-03d2-50eb-80d7-503be84cddfd
| 295,099
|
Let $n, k$ be given positive integers with $n>k$. Prove that
$$
\frac{1}{n+1} \cdot \frac{n^{n}}{k^{k}(n-k)^{n-k}}<\frac{n!}{k!(n-k)!}<\frac{n^{n}}{k^{k}(n-k)^{n-k}} .
$$
|
The inequality is equivalent to
$$
\frac{n^{n}}{n+1}<\binom{n}{k} k^{k}(n-k)^{n-k}<n^{n}
$$
which suggests investigating the binomial expansion of
$$
n^{n}=((n-k)+k)^{n}=\sum_{i=0}^{n}\binom{n}{i}(n-k)^{n-i} k^{i}
$$
The $(k+1)$ th term $T_{k+1}$ of the expansion is $\binom{n}{k} k^{k}(n-k)^{n-k}$, and all terms in the expansion are positive, which implies the right inequality.
Now, for $1 \leq i \leq n$,
$$
\frac{T_{i+1}}{T_{i}}=\frac{\binom{n}{i}(n-k)^{n-i} k^{i}}{\binom{n}{i-1}(n-k)^{n-i+1} k^{i-1}}=\frac{(n-i+1) k}{i(n-k)}
$$
and
$$
\frac{T_{i+1}}{T_{i}}>1 \Longleftrightarrow(n-i+1) k>i(n-k) \Longleftrightarrow i<k+\frac{k}{n} \Longleftrightarrow i \leq k
$$
This means that
$$
T_{1}<T_{2}<\cdots<T_{k+1}>T_{k+2}>\cdots>T_{n+1}
$$
that is, $T_{k+1}=\binom{n}{k} k^{k}(n-k)^{n-k}$ is the largest term in the expansion. The maximum term is greater that the average, which is the sum $n^{n}$ divided by the quantity $n+1$, therefore
$$
\binom{n}{k} k^{k}(n-k)^{n-k}>\frac{n^{n}}{n+1}
$$
as required.
Comment: If we divide further by $n^{n}$ one finds
$$
\frac{1}{n+1}<\binom{n}{k}\left(\frac{k}{n}\right)^{k}\left(1-\frac{k}{n}\right)^{n-k}<1
$$
The middle term is the probability $P(X=k)$ of $k$ successes in a binomial distribution with $n$ trials and success probability $p=\frac{k}{n}$. The right inequality is immediate from the fact that $P(X=k)$ is not the only possible event in this distribution, and the left inequality comes from the fact that the mode of the binomial distribution are given by $\lfloor(n+1) p\rfloor=\left\lfloor(n+1) \frac{k}{n}\right\rfloor=k$ and $\lceil(n+1) p-1\rceil=k$. However, the proof of this fact is identical to the above solution.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n, k$ be given positive integers with $n>k$. Prove that
$$
\frac{1}{n+1} \cdot \frac{n^{n}}{k^{k}(n-k)^{n-k}}<\frac{n!}{k!(n-k)!}<\frac{n^{n}}{k^{k}(n-k)^{n-k}} .
$$
|
The inequality is equivalent to
$$
\frac{n^{n}}{n+1}<\binom{n}{k} k^{k}(n-k)^{n-k}<n^{n}
$$
which suggests investigating the binomial expansion of
$$
n^{n}=((n-k)+k)^{n}=\sum_{i=0}^{n}\binom{n}{i}(n-k)^{n-i} k^{i}
$$
The $(k+1)$ th term $T_{k+1}$ of the expansion is $\binom{n}{k} k^{k}(n-k)^{n-k}$, and all terms in the expansion are positive, which implies the right inequality.
Now, for $1 \leq i \leq n$,
$$
\frac{T_{i+1}}{T_{i}}=\frac{\binom{n}{i}(n-k)^{n-i} k^{i}}{\binom{n}{i-1}(n-k)^{n-i+1} k^{i-1}}=\frac{(n-i+1) k}{i(n-k)}
$$
and
$$
\frac{T_{i+1}}{T_{i}}>1 \Longleftrightarrow(n-i+1) k>i(n-k) \Longleftrightarrow i<k+\frac{k}{n} \Longleftrightarrow i \leq k
$$
This means that
$$
T_{1}<T_{2}<\cdots<T_{k+1}>T_{k+2}>\cdots>T_{n+1}
$$
that is, $T_{k+1}=\binom{n}{k} k^{k}(n-k)^{n-k}$ is the largest term in the expansion. The maximum term is greater that the average, which is the sum $n^{n}$ divided by the quantity $n+1$, therefore
$$
\binom{n}{k} k^{k}(n-k)^{n-k}>\frac{n^{n}}{n+1}
$$
as required.
Comment: If we divide further by $n^{n}$ one finds
$$
\frac{1}{n+1}<\binom{n}{k}\left(\frac{k}{n}\right)^{k}\left(1-\frac{k}{n}\right)^{n-k}<1
$$
The middle term is the probability $P(X=k)$ of $k$ successes in a binomial distribution with $n$ trials and success probability $p=\frac{k}{n}$. The right inequality is immediate from the fact that $P(X=k)$ is not the only possible event in this distribution, and the left inequality comes from the fact that the mode of the binomial distribution are given by $\lfloor(n+1) p\rfloor=\left\lfloor(n+1) \frac{k}{n}\right\rfloor=k$ and $\lceil(n+1) p-1\rceil=k$. However, the proof of this fact is identical to the above solution.
|
{
"resource_path": "APMO/segmented/en-apmo2000_sol.jsonl",
"problem_match": "# Problem 4",
"solution_match": "# Solution\n\n"
}
|
8f67957e-a757-5eb8-81fd-23175a1dd233
| 604,792
|
Given a permutation $\left(a_{0}, a_{1}, \ldots, a_{n}\right)$ of the sequence $0,1, \ldots, n$. A transposition of $a_{i}$ with $a_{j}$ is called legal if $a_{i}=0$ for $i>0$, and $a_{i-1}+1=a_{j}$. The permutation $\left(a_{0}, a_{1}, \ldots, a_{n}\right)$ is called regular if after a number of legal transpositions it becomes $(1,2, \ldots, n, 0)$. For which numbers $n$ is the permutation $(1, n, n-1, \ldots, 3,2,0)$ regular?
Answer: $n=2$ and $n=2^{k}-1, k$ positive integer.
|
A legal transposition consists of looking at the number immediately before 0 and exchanging 0 and its successor; therefore, we can perform at most one legal transposition to any permutation, and a legal transposition is not possible only and if only 0 is preceded by $n$.
If $n=1$ or $n=2$ there is nothing to do, so $n=1=2^{1}-1$ and $n=2$ are solutions. Suppose that $n>3$ in the following.
Call a pass a maximal sequence of legal transpositions that move 0 to the left. We first illustrate what happens in the case $n=15$, which is large enough to visualize what is going on. The first pass is
$$
\begin{aligned}
& (1,15,14,13,12,11,10,9,8,7,6,5,4,3,2,0) \\
& (1,15,14,13,12,11,10,9,8,7,6,5,4,0,2,3) \\
& (1,15,14,13,12,11,10,9,8,7,6,0,4,5,2,3) \\
& (1,15,14,13,12,11,10,9,8,0,6,7,4,5,2,3) \\
& (1,15,14,13,12,11,10,0,8,9,6,7,4,5,2,3) \\
& (1,15,14,13,12,0,10,11,8,9,6,7,4,5,2,3) \\
& (1,15,14,0,12,13,10,11,8,9,6,7,4,5,2,3) \\
& (1,0,14,15,12,13,10,11,8,9,6,7,4,5,2,3)
\end{aligned}
$$
After exchanging 0 and 2, the second pass is
$$
\begin{aligned}
& (1,2,14,15,12,13,10,11,8,9,6,7,4,5,0,3) \\
& (1,2,14,15,12,13, \mathbf{1 0}, 11,8,9,0,7,4,5,6,3) \\
& (1,2, \mathbf{1 4}, 15,12,13,0,11,8,9,10,7,4,5,6,3) \\
& (1,2,0,15,12,13,14,11,8,9,10,7,4,5,6,3)
\end{aligned}
$$
After exchanging 0 and 3 , the third pass is
$$
\begin{aligned}
& (1,2,3,15,12,13,14,11,8,9,10,7,4,5,6,0) \\
& (1,2,3,15,12,13,14,11,8,9,10,0,4,5,6,7) \\
& (1,2,3,15,12,13,14,0,8,9,10,11,4,5,6,7) \\
& (1,2,3,0,12,13,14,15,8,9,10,11,4,5,6,7)
\end{aligned}
$$
After exchanging 0 and 4, the fourth pass is
$$
\begin{aligned}
& (1,2,3,4,12,13,14,15,8,9,10,11,0,5,6,7) \\
& (1,2,3,4,0,13,14,15,8,9,10,11,12,5,6,7)
\end{aligned}
$$
And then one can successively perform the operations to eventually find
$$
(1,2,3,4,5,6,7,0,8,9,10,11,12,13,14,15)
$$
after which 0 will move one unit to the right with each transposition, and $n=15$ is a solution. The general case follows.
Case 1: $n>2$ even: After the first pass, in which 0 is transposed successively with $3,5, \ldots, n-1$, after which 0 is right after $n$, and no other legal transposition can be performed. So $n$ is not a solution in this case.
Case 2: $n=2^{k}-1$ : Denote $N=n+1, R=2^{r},[a: b]=(a, a+1, a+2, \ldots, b)$, and concatenation by a comma. Let $P_{r}$ be the permutation
$$
[1: R-1],(0),[N-R: N-1],[N-2 R: N-R-1], \ldots,[2 R: 3 R-1],[R: 2 R-1]
$$
$P_{r}$ is formed by the blocks $[1: R-1],(0)$, and other $2^{k-r}-1$ blocks of size $R=2^{r}$ with consecutive numbers, beginning with $t R$ and finishing with $(t+1) R-1$, in decreasing order of $t$. Also define $P_{0}$ as the initial permutation.
Then it can be verified that $P_{r+1}$ is obtained from $P_{r}$ after a number of legal transpositions: it can be easily verified that $P_{0}$ leads to $P_{1}$, as 0 is transposed successively with $3,5, \ldots, n-1$, shifting cyclically all numbers with even indices; this is $P_{1}$.
Starting from $P_{r}, r>0$, 0 is successively transposed with $R, 3 R, \ldots, N-R$. The numbers $0, N-R, N-3 R, \ldots, 3 R, R$ are cyclically shifted. This means that $R$ precedes 0 , and the blocks become
$$
\begin{gathered}
{[1: R],(0),[N-R+1: N-1],[N-2 R: N-R],[N-3 R+1: N-2 R-1], \ldots,} \\
{[3 R+1: 4 R-1],[2 R: 3 R],[R+1: 2 R-1]}
\end{gathered}
$$
Note that the first block and the ones on even positions greater than 2 have one more number and the other blocks have one less number.
Now $0, N-R+1, N-3 R+1, \ldots, 3 R+1, R+1$ are shifted. Note that, for every $i$ th block, $i$ odd greater than 1 , the first number is cyclically shifted, and the blocks become
$$
\begin{gathered}
{[1: R+1],(0),[N-R+2: N-1],[N-2 R: N-R+1],[N-3 R+2: N-2 R-1], \ldots,} \\
{[3 R+1: 4 R-1],[2 R: 3 R+1],[R+2: 2 R-1]}
\end{gathered}
$$
The same phenomenom happened: the first block and the ones on even positions greater than 2 have one more number and the other blocks have one less number. This pattern continues: $0, N-R+u, N-3 R+u, \ldots, R+u$ are shifted, $u=0,1,2, \ldots, R-1$, the first block and the ones on even positions greater than 2 have one more number and the other blocks have one less number, until they vanish. We finish with
$$
[1: 2 R-1],(0),[N-2 R: N-1], \ldots,[2 R: 4 R-1]
$$
which is precisely $P_{r+1}$.
Since $P_{k}=[1: N-1],(0), n=2^{k}-1$ is a solution.
Case 3: $n$ is odd, but is not of the form $2^{k}-1$. Write $n+1$ as $n+1=2^{a}(2 b+1), b \geq 1$, and define $P_{0}, \ldots, P_{a}$ as in the previous case. Since $2^{a}$ divides $N=n+1$, the same rules apply, and we obtain $P_{a}$ :
$$
\left[1: 2^{a}-1\right],(0),\left[N-2^{a}: N-1\right],\left[N-2^{a+1}: N-2^{a}-1\right], \ldots,\left[2^{a+1}: 3 \cdot 2^{a}-1\right],\left[2^{a}: 2^{a+1}-1\right]
$$
But then 0 is transposed with $2^{a}, 3 \cdot 2^{a}, \ldots,(2 b-1) \cdot 2^{a}=N-2^{a+1}$, after which 0 is put immediately after $N-1=n$, and cannot be transposed again. Therefore, $n$ is not a solution. All cases were studied, and so we are done.
Comment: The general problem of finding the number of regular permutations for any $n$ seems to be difficult. A computer finds the first few values
$$
1,2,5,14,47,189,891,4815,29547
$$
which is not catalogued at oeis.org.
|
n=2 \text{ and } n=2^{k}-1, k \text{ positive integer}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Given a permutation $\left(a_{0}, a_{1}, \ldots, a_{n}\right)$ of the sequence $0,1, \ldots, n$. A transposition of $a_{i}$ with $a_{j}$ is called legal if $a_{i}=0$ for $i>0$, and $a_{i-1}+1=a_{j}$. The permutation $\left(a_{0}, a_{1}, \ldots, a_{n}\right)$ is called regular if after a number of legal transpositions it becomes $(1,2, \ldots, n, 0)$. For which numbers $n$ is the permutation $(1, n, n-1, \ldots, 3,2,0)$ regular?
Answer: $n=2$ and $n=2^{k}-1, k$ positive integer.
|
A legal transposition consists of looking at the number immediately before 0 and exchanging 0 and its successor; therefore, we can perform at most one legal transposition to any permutation, and a legal transposition is not possible only and if only 0 is preceded by $n$.
If $n=1$ or $n=2$ there is nothing to do, so $n=1=2^{1}-1$ and $n=2$ are solutions. Suppose that $n>3$ in the following.
Call a pass a maximal sequence of legal transpositions that move 0 to the left. We first illustrate what happens in the case $n=15$, which is large enough to visualize what is going on. The first pass is
$$
\begin{aligned}
& (1,15,14,13,12,11,10,9,8,7,6,5,4,3,2,0) \\
& (1,15,14,13,12,11,10,9,8,7,6,5,4,0,2,3) \\
& (1,15,14,13,12,11,10,9,8,7,6,0,4,5,2,3) \\
& (1,15,14,13,12,11,10,9,8,0,6,7,4,5,2,3) \\
& (1,15,14,13,12,11,10,0,8,9,6,7,4,5,2,3) \\
& (1,15,14,13,12,0,10,11,8,9,6,7,4,5,2,3) \\
& (1,15,14,0,12,13,10,11,8,9,6,7,4,5,2,3) \\
& (1,0,14,15,12,13,10,11,8,9,6,7,4,5,2,3)
\end{aligned}
$$
After exchanging 0 and 2, the second pass is
$$
\begin{aligned}
& (1,2,14,15,12,13,10,11,8,9,6,7,4,5,0,3) \\
& (1,2,14,15,12,13, \mathbf{1 0}, 11,8,9,0,7,4,5,6,3) \\
& (1,2, \mathbf{1 4}, 15,12,13,0,11,8,9,10,7,4,5,6,3) \\
& (1,2,0,15,12,13,14,11,8,9,10,7,4,5,6,3)
\end{aligned}
$$
After exchanging 0 and 3 , the third pass is
$$
\begin{aligned}
& (1,2,3,15,12,13,14,11,8,9,10,7,4,5,6,0) \\
& (1,2,3,15,12,13,14,11,8,9,10,0,4,5,6,7) \\
& (1,2,3,15,12,13,14,0,8,9,10,11,4,5,6,7) \\
& (1,2,3,0,12,13,14,15,8,9,10,11,4,5,6,7)
\end{aligned}
$$
After exchanging 0 and 4, the fourth pass is
$$
\begin{aligned}
& (1,2,3,4,12,13,14,15,8,9,10,11,0,5,6,7) \\
& (1,2,3,4,0,13,14,15,8,9,10,11,12,5,6,7)
\end{aligned}
$$
And then one can successively perform the operations to eventually find
$$
(1,2,3,4,5,6,7,0,8,9,10,11,12,13,14,15)
$$
after which 0 will move one unit to the right with each transposition, and $n=15$ is a solution. The general case follows.
Case 1: $n>2$ even: After the first pass, in which 0 is transposed successively with $3,5, \ldots, n-1$, after which 0 is right after $n$, and no other legal transposition can be performed. So $n$ is not a solution in this case.
Case 2: $n=2^{k}-1$ : Denote $N=n+1, R=2^{r},[a: b]=(a, a+1, a+2, \ldots, b)$, and concatenation by a comma. Let $P_{r}$ be the permutation
$$
[1: R-1],(0),[N-R: N-1],[N-2 R: N-R-1], \ldots,[2 R: 3 R-1],[R: 2 R-1]
$$
$P_{r}$ is formed by the blocks $[1: R-1],(0)$, and other $2^{k-r}-1$ blocks of size $R=2^{r}$ with consecutive numbers, beginning with $t R$ and finishing with $(t+1) R-1$, in decreasing order of $t$. Also define $P_{0}$ as the initial permutation.
Then it can be verified that $P_{r+1}$ is obtained from $P_{r}$ after a number of legal transpositions: it can be easily verified that $P_{0}$ leads to $P_{1}$, as 0 is transposed successively with $3,5, \ldots, n-1$, shifting cyclically all numbers with even indices; this is $P_{1}$.
Starting from $P_{r}, r>0$, 0 is successively transposed with $R, 3 R, \ldots, N-R$. The numbers $0, N-R, N-3 R, \ldots, 3 R, R$ are cyclically shifted. This means that $R$ precedes 0 , and the blocks become
$$
\begin{gathered}
{[1: R],(0),[N-R+1: N-1],[N-2 R: N-R],[N-3 R+1: N-2 R-1], \ldots,} \\
{[3 R+1: 4 R-1],[2 R: 3 R],[R+1: 2 R-1]}
\end{gathered}
$$
Note that the first block and the ones on even positions greater than 2 have one more number and the other blocks have one less number.
Now $0, N-R+1, N-3 R+1, \ldots, 3 R+1, R+1$ are shifted. Note that, for every $i$ th block, $i$ odd greater than 1 , the first number is cyclically shifted, and the blocks become
$$
\begin{gathered}
{[1: R+1],(0),[N-R+2: N-1],[N-2 R: N-R+1],[N-3 R+2: N-2 R-1], \ldots,} \\
{[3 R+1: 4 R-1],[2 R: 3 R+1],[R+2: 2 R-1]}
\end{gathered}
$$
The same phenomenom happened: the first block and the ones on even positions greater than 2 have one more number and the other blocks have one less number. This pattern continues: $0, N-R+u, N-3 R+u, \ldots, R+u$ are shifted, $u=0,1,2, \ldots, R-1$, the first block and the ones on even positions greater than 2 have one more number and the other blocks have one less number, until they vanish. We finish with
$$
[1: 2 R-1],(0),[N-2 R: N-1], \ldots,[2 R: 4 R-1]
$$
which is precisely $P_{r+1}$.
Since $P_{k}=[1: N-1],(0), n=2^{k}-1$ is a solution.
Case 3: $n$ is odd, but is not of the form $2^{k}-1$. Write $n+1$ as $n+1=2^{a}(2 b+1), b \geq 1$, and define $P_{0}, \ldots, P_{a}$ as in the previous case. Since $2^{a}$ divides $N=n+1$, the same rules apply, and we obtain $P_{a}$ :
$$
\left[1: 2^{a}-1\right],(0),\left[N-2^{a}: N-1\right],\left[N-2^{a+1}: N-2^{a}-1\right], \ldots,\left[2^{a+1}: 3 \cdot 2^{a}-1\right],\left[2^{a}: 2^{a+1}-1\right]
$$
But then 0 is transposed with $2^{a}, 3 \cdot 2^{a}, \ldots,(2 b-1) \cdot 2^{a}=N-2^{a+1}$, after which 0 is put immediately after $N-1=n$, and cannot be transposed again. Therefore, $n$ is not a solution. All cases were studied, and so we are done.
Comment: The general problem of finding the number of regular permutations for any $n$ seems to be difficult. A computer finds the first few values
$$
1,2,5,14,47,189,891,4815,29547
$$
which is not catalogued at oeis.org.
|
{
"resource_path": "APMO/segmented/en-apmo2000_sol.jsonl",
"problem_match": "# Problem 5",
"solution_match": "# Solution\n\n"
}
|
ee71701f-3b05-5cca-8120-feb60e11a885
| 604,810
|
Let $a_{1}, a_{2}, a_{3}, \ldots, a_{n}$ be a sequence of non-negative integers, where $n$ is a positive integer.
Let
$$
A_{n}=\frac{a_{1}+a_{2}+\cdots+a_{n}}{n}
$$
Prove that
$$
a_{1}!a_{2}!\ldots a_{n}!\geq\left(\left\lfloor A_{n}\right\rfloor!\right)^{n}
$$
where $\left\lfloor A_{n}\right\rfloor$ is the greatest integer less than or equal to $A_{n}$, and $a!=1 \times 2 \times \cdots \times a$ for $a \geq 1$ (and $0!=1$ ). When does equality hold?
|
Assume without loss of generality that $a_{1} \geq a_{2} \geq \cdots \geq a_{n} \geq 0$, and let $s=\left\lfloor A_{n}\right\rfloor$. Let $k$ be any (fixed) index for which $a_{k} \geq s \geq a_{k+1}$.
Our inequality is equivalent to proving that
$$
\frac{a_{1}!}{s!} \cdot \frac{a_{2}!}{s!} \cdot \ldots \cdot \frac{a_{k}!}{s!} \geq \frac{s!}{a_{k+1}!} \cdot \frac{s!}{a_{k+2}!} \cdot \ldots \cdot \frac{s!}{a_{n}!}
$$
Now for $i=1,2, \ldots, k, a_{i}!/ s!$ is the product of $a_{i}-s$ factors. For example, 9!/5! $=9 \cdot 8 \cdot 7 \cdot 6$. The left side of inequality (1) therefore is the product of $A=a_{1}+a_{2}+\cdots+a_{k}-k s$ factors, all of which are greater than $s$. Similarly, the right side of (1) is the product of $B=(n-k) s-$ $\left(a_{k+1}+a_{k+2}+\cdots+a_{n}\right)$ factors, all of which are at most $s$. Since $\sum_{i=1}^{n} a_{i}=n A_{n} \geq n s, A \geq B$. This proves the inequality. [ 5 marks to here.]
Equality in (1) holds if and only if either:
(i) $A=B=0$, that is, both sides of (1) are the empty product, which occurs if and only if $a_{1}=a_{2}=\cdots=a_{n}$; or
(ii) $a_{1}=1$ and $s=0$, that is, the only factors on either side of (1) are 1 's, which occurs if and only if $a_{i} \in\{0,1\}$ for all $i$. [2 marks for both (i) and (ii), no marks for (i) only.]
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a_{1}, a_{2}, a_{3}, \ldots, a_{n}$ be a sequence of non-negative integers, where $n$ is a positive integer.
Let
$$
A_{n}=\frac{a_{1}+a_{2}+\cdots+a_{n}}{n}
$$
Prove that
$$
a_{1}!a_{2}!\ldots a_{n}!\geq\left(\left\lfloor A_{n}\right\rfloor!\right)^{n}
$$
where $\left\lfloor A_{n}\right\rfloor$ is the greatest integer less than or equal to $A_{n}$, and $a!=1 \times 2 \times \cdots \times a$ for $a \geq 1$ (and $0!=1$ ). When does equality hold?
|
Assume without loss of generality that $a_{1} \geq a_{2} \geq \cdots \geq a_{n} \geq 0$, and let $s=\left\lfloor A_{n}\right\rfloor$. Let $k$ be any (fixed) index for which $a_{k} \geq s \geq a_{k+1}$.
Our inequality is equivalent to proving that
$$
\frac{a_{1}!}{s!} \cdot \frac{a_{2}!}{s!} \cdot \ldots \cdot \frac{a_{k}!}{s!} \geq \frac{s!}{a_{k+1}!} \cdot \frac{s!}{a_{k+2}!} \cdot \ldots \cdot \frac{s!}{a_{n}!}
$$
Now for $i=1,2, \ldots, k, a_{i}!/ s!$ is the product of $a_{i}-s$ factors. For example, 9!/5! $=9 \cdot 8 \cdot 7 \cdot 6$. The left side of inequality (1) therefore is the product of $A=a_{1}+a_{2}+\cdots+a_{k}-k s$ factors, all of which are greater than $s$. Similarly, the right side of (1) is the product of $B=(n-k) s-$ $\left(a_{k+1}+a_{k+2}+\cdots+a_{n}\right)$ factors, all of which are at most $s$. Since $\sum_{i=1}^{n} a_{i}=n A_{n} \geq n s, A \geq B$. This proves the inequality. [ 5 marks to here.]
Equality in (1) holds if and only if either:
(i) $A=B=0$, that is, both sides of (1) are the empty product, which occurs if and only if $a_{1}=a_{2}=\cdots=a_{n}$; or
(ii) $a_{1}=1$ and $s=0$, that is, the only factors on either side of (1) are 1 's, which occurs if and only if $a_{i} \in\{0,1\}$ for all $i$. [2 marks for both (i) and (ii), no marks for (i) only.]
|
{
"resource_path": "APMO/segmented/en-apmo2002_sol.jsonl",
"problem_match": "\n1. ",
"solution_match": "# Solution 1."
}
|
7d52eb5a-0c52-5bc1-a0a3-cce54fdf8e25
| 607,114
|
Let $a_{1}, a_{2}, a_{3}, \ldots, a_{n}$ be a sequence of non-negative integers, where $n$ is a positive integer.
Let
$$
A_{n}=\frac{a_{1}+a_{2}+\cdots+a_{n}}{n}
$$
Prove that
$$
a_{1}!a_{2}!\ldots a_{n}!\geq\left(\left\lfloor A_{n}\right\rfloor!\right)^{n}
$$
where $\left\lfloor A_{n}\right\rfloor$ is the greatest integer less than or equal to $A_{n}$, and $a!=1 \times 2 \times \cdots \times a$ for $a \geq 1$ (and $0!=1$ ). When does equality hold?
|
Assume without loss of generality that $0 \leq a_{1} \leq a_{2} \leq \cdots \leq a_{n}$. Let $d=a_{n}-a_{1}$ and $m=\left|\left\{i: a_{i}=a_{1}\right\}\right|$. Our proof is by induction on $d$.
We first do the case $d=a_{n}-a_{1}=0$ or 1 separately. Then $a_{1}=a_{2}=\cdots=a_{m}=a$ and $a_{m+1}=\cdots=a_{n}=a+1$ for some $1 \leq m \leq n$ and $a \geq 0$. In this case we have $\left\lfloor A_{n}\right\rfloor=a$, so the inequality to be proven is just $a_{1}!a_{2}!\ldots a_{n}!\geq(a!)^{n}$, which is obvious. Equality holds if and only if either $m=n$, that is, $a_{1}=a_{2}=\cdots=a_{n}=a$; or if $a=0$, that is, $a_{1}=\cdots=a_{m}=0$ and $a_{m+1}=\cdots=a_{n}=1$. [ 2 marks to here.]
So assume that $d=a_{n}-a_{1} \geq 2$ and that the inequality holds for all sequences with smaller values of $d$, or with the same value of $d$ and smaller values of $m$. Then the sequence
$$
a_{1}+1, a_{2}, a_{3}, \ldots, a_{n-1}, a_{n}-1
$$
though not necessarily in non-decreasing order any more, does have either a smaller value of $d$, or the same value of $d$ and a smaller value of $m$, but in any case has the same value of $A_{n}$. Thus, by induction and since $a_{n}>a_{1}+1$,
$$
\begin{aligned}
a_{1}!a_{2}!\ldots a_{n}! & =\left(a_{1}+1\right)!a_{2}!\ldots a_{n-1}!\left(a_{n}-1\right)!\cdot \frac{a_{n}}{a_{1}+1} \\
& \geq\left(\left\lfloor A_{n}\right\rfloor!\right)^{n} \cdot \frac{a_{n}}{a_{1}+1} \\
& >\left(\left\lfloor A_{n}\right\rfloor!\right)^{n}
\end{aligned}
$$
which completes the proof. Equality cannot hold in this case.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a_{1}, a_{2}, a_{3}, \ldots, a_{n}$ be a sequence of non-negative integers, where $n$ is a positive integer.
Let
$$
A_{n}=\frac{a_{1}+a_{2}+\cdots+a_{n}}{n}
$$
Prove that
$$
a_{1}!a_{2}!\ldots a_{n}!\geq\left(\left\lfloor A_{n}\right\rfloor!\right)^{n}
$$
where $\left\lfloor A_{n}\right\rfloor$ is the greatest integer less than or equal to $A_{n}$, and $a!=1 \times 2 \times \cdots \times a$ for $a \geq 1$ (and $0!=1$ ). When does equality hold?
|
Assume without loss of generality that $0 \leq a_{1} \leq a_{2} \leq \cdots \leq a_{n}$. Let $d=a_{n}-a_{1}$ and $m=\left|\left\{i: a_{i}=a_{1}\right\}\right|$. Our proof is by induction on $d$.
We first do the case $d=a_{n}-a_{1}=0$ or 1 separately. Then $a_{1}=a_{2}=\cdots=a_{m}=a$ and $a_{m+1}=\cdots=a_{n}=a+1$ for some $1 \leq m \leq n$ and $a \geq 0$. In this case we have $\left\lfloor A_{n}\right\rfloor=a$, so the inequality to be proven is just $a_{1}!a_{2}!\ldots a_{n}!\geq(a!)^{n}$, which is obvious. Equality holds if and only if either $m=n$, that is, $a_{1}=a_{2}=\cdots=a_{n}=a$; or if $a=0$, that is, $a_{1}=\cdots=a_{m}=0$ and $a_{m+1}=\cdots=a_{n}=1$. [ 2 marks to here.]
So assume that $d=a_{n}-a_{1} \geq 2$ and that the inequality holds for all sequences with smaller values of $d$, or with the same value of $d$ and smaller values of $m$. Then the sequence
$$
a_{1}+1, a_{2}, a_{3}, \ldots, a_{n-1}, a_{n}-1
$$
though not necessarily in non-decreasing order any more, does have either a smaller value of $d$, or the same value of $d$ and a smaller value of $m$, but in any case has the same value of $A_{n}$. Thus, by induction and since $a_{n}>a_{1}+1$,
$$
\begin{aligned}
a_{1}!a_{2}!\ldots a_{n}! & =\left(a_{1}+1\right)!a_{2}!\ldots a_{n-1}!\left(a_{n}-1\right)!\cdot \frac{a_{n}}{a_{1}+1} \\
& \geq\left(\left\lfloor A_{n}\right\rfloor!\right)^{n} \cdot \frac{a_{n}}{a_{1}+1} \\
& >\left(\left\lfloor A_{n}\right\rfloor!\right)^{n}
\end{aligned}
$$
which completes the proof. Equality cannot hold in this case.
|
{
"resource_path": "APMO/segmented/en-apmo2002_sol.jsonl",
"problem_match": "\n1. ",
"solution_match": "\nSolution 2."
}
|
7d52eb5a-0c52-5bc1-a0a3-cce54fdf8e25
| 607,114
|
Find all positive integers $a$ and $b$ such that
$$
\frac{a^{2}+b}{b^{2}-a} \text { and } \frac{b^{2}+a}{a^{2}-b}
$$
are both integers.
|
By the symmetry of the problem, we may suppose that $a \leq b$. Notice that $b^{2}-a \geq 0$, so that if $\frac{a^{2}+b}{b^{2}-a}$ is a positive integer, then $a^{2}+b \geq b^{2}-a$. Rearranging this inequality and factorizing, we find that $(a+b)(a-b+1) \geq 0$. Since $a, b>0$, we must have $a \geq b-1$. [3 marks to here.] We therefore have two cases:
Case 1: $a=b$. Substituting, we have
$$
\frac{a^{2}+a}{a^{2}-a}=\frac{a+1}{a-1}=1+\frac{2}{a-1},
$$
which is an integer if and only if $(a-1) \mid 2$. As $a>0$, the only possible values are $a-1=1$ or 2. Hence, $(a, b)=(2,2)$ or $(3,3)$. [1 mark.]
Case 2: $a=b-1$. Substituting, we have
$$
\frac{b^{2}+a}{a^{2}-b}=\frac{(a+1)^{2}+a}{a^{2}-(a+1)}=\frac{a^{2}+3 a+1}{a^{2}-a-1}=1+\frac{4 a+2}{a^{2}-a-1} .
$$
Once again, notice that $4 a+2>0$, and hence, for $\frac{4 a+2}{a^{2}-a-1}$ to be an integer, we must have $4 a+2 \geq a^{2}-a-1$, that is, $a^{2}-5 a-3 \leq 0$. Hence, since $a$ is an integer, we can bound $a$ by $1 \leq \bar{a} \leq 5$. Checking all the ordered pairs $(a, b)=(1,2),(2,3), \ldots,(5,6)$, we find that only $(1,2)$ and $(2,3)$ satisfy the given conditions. [3 marks.]
Thus, the ordered pairs that work are
$$
(2,2),(3,3),(1,2),(2,3),(2,1),(3,2)
$$
where the last two pairs follow by symmetry. [2 marks if these solutions are found without proof that there are no others.]
|
(2,2),(3,3),(1,2),(2,3),(2,1),(3,2)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all positive integers $a$ and $b$ such that
$$
\frac{a^{2}+b}{b^{2}-a} \text { and } \frac{b^{2}+a}{a^{2}-b}
$$
are both integers.
|
By the symmetry of the problem, we may suppose that $a \leq b$. Notice that $b^{2}-a \geq 0$, so that if $\frac{a^{2}+b}{b^{2}-a}$ is a positive integer, then $a^{2}+b \geq b^{2}-a$. Rearranging this inequality and factorizing, we find that $(a+b)(a-b+1) \geq 0$. Since $a, b>0$, we must have $a \geq b-1$. [3 marks to here.] We therefore have two cases:
Case 1: $a=b$. Substituting, we have
$$
\frac{a^{2}+a}{a^{2}-a}=\frac{a+1}{a-1}=1+\frac{2}{a-1},
$$
which is an integer if and only if $(a-1) \mid 2$. As $a>0$, the only possible values are $a-1=1$ or 2. Hence, $(a, b)=(2,2)$ or $(3,3)$. [1 mark.]
Case 2: $a=b-1$. Substituting, we have
$$
\frac{b^{2}+a}{a^{2}-b}=\frac{(a+1)^{2}+a}{a^{2}-(a+1)}=\frac{a^{2}+3 a+1}{a^{2}-a-1}=1+\frac{4 a+2}{a^{2}-a-1} .
$$
Once again, notice that $4 a+2>0$, and hence, for $\frac{4 a+2}{a^{2}-a-1}$ to be an integer, we must have $4 a+2 \geq a^{2}-a-1$, that is, $a^{2}-5 a-3 \leq 0$. Hence, since $a$ is an integer, we can bound $a$ by $1 \leq \bar{a} \leq 5$. Checking all the ordered pairs $(a, b)=(1,2),(2,3), \ldots,(5,6)$, we find that only $(1,2)$ and $(2,3)$ satisfy the given conditions. [3 marks.]
Thus, the ordered pairs that work are
$$
(2,2),(3,3),(1,2),(2,3),(2,1),(3,2)
$$
where the last two pairs follow by symmetry. [2 marks if these solutions are found without proof that there are no others.]
|
{
"resource_path": "APMO/segmented/en-apmo2002_sol.jsonl",
"problem_match": "\n2. ",
"solution_match": "\nSolution."
}
|
650b03c5-f303-531e-9148-421c94a8e535
| 607,115
|
Let $A B C$ be an equilateral triangle. Let $P$ be a point on the side $A C$ and $Q$ be a point on the side $A B$ so that both triangles $A B P$ and $A C Q$ are acute. Let $R$ be the orthocentre of triangle $A B P$ and $S$ be the orthocentre of triangle $A C Q$. Let $T$ be the point common to the segments $B P$ and $C Q$. Find all possible values of $\angle C B P$ and $\angle B C Q$ such that triangle $T R S$ is equilateral.
|
We are going to show that this can only happen when
$$
\angle C B P=\angle B C Q=15^{\circ} .
$$
Lemma. If $\angle C B P>\angle B C Q$, then $R T>S T$.
Proof. Let $A D, B E$ and $C F$ be the altitudes of triangle $A B C$ concurrent at its centre $G$. Then $P$ lies on $C E, Q$ lies on $B F$, and thus $T$ lies in triangle $B D G$.
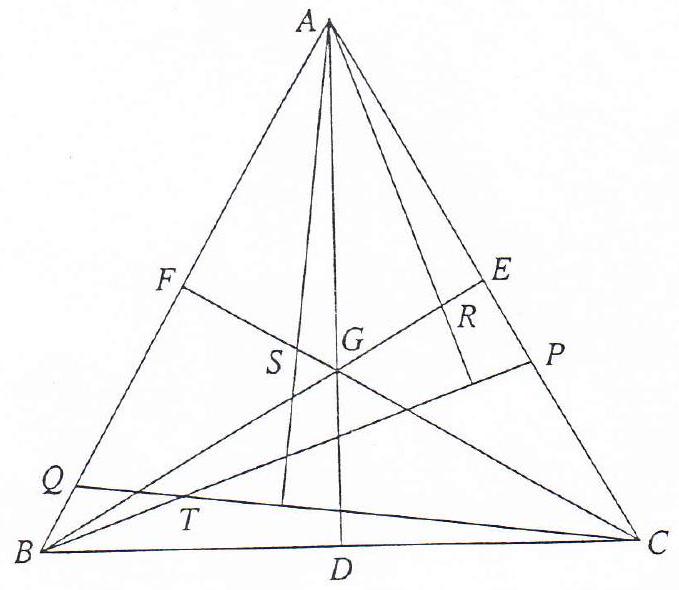
Note that -
$$
\angle F A S=\angle F C Q=30^{\circ}-\angle B C Q>30^{\circ}-\angle C B P=\angle E B P=\angle E A R
$$
Since $A F=A E$, we have $F S>E R$ so that
$$
G S=G F-F S<G E-E R=G R .
$$
Let $T_{x}$ be the projection of $T$ onto $B C$ and $T_{y}$ be the projection of $T$ onto $A D$, and similarly for $R$ and $S$. We have
$$
R_{x} T_{x}=D R_{x}+D T_{x}>\left|D S_{x}-D T_{x}\right|=S_{x} T_{x}
$$
and
$$
R_{y} T_{y}=G R_{y}+G T_{y}>G S_{y}+G T_{y}=S_{y} T_{y}
$$
It follows that $R T>S T$.
[1 mark for stating the Lemma, 3 marks for proving it.]
Thus, if $\triangle T R S$ is equilateral, we must have $\angle C B P=\angle B C Q$.
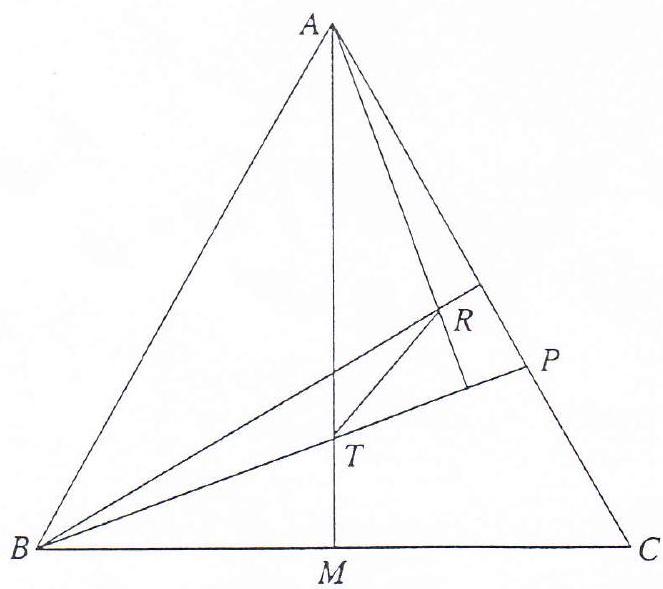
It is clear from the symmetry of the figure that $T R=T S$, so $\triangle T R S$ is equilateral if and only if $\angle R T A=30^{\circ}$. Now, as $B R$ is an altitude of the triangle $A B C, \angle R B A=30^{\circ}$. So $\triangle T R S$ is equilateral if and only if $R T B A$ is a cyclic quadrilateral. Therefore, $\triangle T R S$ is equilateral if and only if $\angle T B R=\angle T A R$. But
$$
\begin{aligned}
90^{\circ} & =\angle T B A+\angle B A R \\
& =(\angle T B R+\angle R B A)+(\angle B A T+\angle T A R) \\
& =\left(\angle T B R+30^{\circ}\right)+\left(30^{\circ}+\angle T A R\right)
\end{aligned}
$$
and so
$$
30^{\circ}=\angle T A R+\angle T B R
$$
But these angles must be equal, so $\angle T A R=\angle T B R=15^{\circ}$. Therefore $\angle C B P=\angle B C Q=15^{\circ}$. [3 marks for finishing the proof with the assumption that $\angle C B P=\angle B C Q$.]
|
\angle C B P=\angle B C Q=15^{\circ}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be an equilateral triangle. Let $P$ be a point on the side $A C$ and $Q$ be a point on the side $A B$ so that both triangles $A B P$ and $A C Q$ are acute. Let $R$ be the orthocentre of triangle $A B P$ and $S$ be the orthocentre of triangle $A C Q$. Let $T$ be the point common to the segments $B P$ and $C Q$. Find all possible values of $\angle C B P$ and $\angle B C Q$ such that triangle $T R S$ is equilateral.
|
We are going to show that this can only happen when
$$
\angle C B P=\angle B C Q=15^{\circ} .
$$
Lemma. If $\angle C B P>\angle B C Q$, then $R T>S T$.
Proof. Let $A D, B E$ and $C F$ be the altitudes of triangle $A B C$ concurrent at its centre $G$. Then $P$ lies on $C E, Q$ lies on $B F$, and thus $T$ lies in triangle $B D G$.

Note that -
$$
\angle F A S=\angle F C Q=30^{\circ}-\angle B C Q>30^{\circ}-\angle C B P=\angle E B P=\angle E A R
$$
Since $A F=A E$, we have $F S>E R$ so that
$$
G S=G F-F S<G E-E R=G R .
$$
Let $T_{x}$ be the projection of $T$ onto $B C$ and $T_{y}$ be the projection of $T$ onto $A D$, and similarly for $R$ and $S$. We have
$$
R_{x} T_{x}=D R_{x}+D T_{x}>\left|D S_{x}-D T_{x}\right|=S_{x} T_{x}
$$
and
$$
R_{y} T_{y}=G R_{y}+G T_{y}>G S_{y}+G T_{y}=S_{y} T_{y}
$$
It follows that $R T>S T$.
[1 mark for stating the Lemma, 3 marks for proving it.]
Thus, if $\triangle T R S$ is equilateral, we must have $\angle C B P=\angle B C Q$.

It is clear from the symmetry of the figure that $T R=T S$, so $\triangle T R S$ is equilateral if and only if $\angle R T A=30^{\circ}$. Now, as $B R$ is an altitude of the triangle $A B C, \angle R B A=30^{\circ}$. So $\triangle T R S$ is equilateral if and only if $R T B A$ is a cyclic quadrilateral. Therefore, $\triangle T R S$ is equilateral if and only if $\angle T B R=\angle T A R$. But
$$
\begin{aligned}
90^{\circ} & =\angle T B A+\angle B A R \\
& =(\angle T B R+\angle R B A)+(\angle B A T+\angle T A R) \\
& =\left(\angle T B R+30^{\circ}\right)+\left(30^{\circ}+\angle T A R\right)
\end{aligned}
$$
and so
$$
30^{\circ}=\angle T A R+\angle T B R
$$
But these angles must be equal, so $\angle T A R=\angle T B R=15^{\circ}$. Therefore $\angle C B P=\angle B C Q=15^{\circ}$. [3 marks for finishing the proof with the assumption that $\angle C B P=\angle B C Q$.]
|
{
"resource_path": "APMO/segmented/en-apmo2002_sol.jsonl",
"problem_match": "\n3. ",
"solution_match": "# Solution."
}
|
7da70825-10b6-50ee-b3db-416f632cec86
| 607,116
|
Let $x, y, z$ be positive numbers such that
$$
\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1
$$
Show that
$$
\sqrt{x+y z}+\sqrt{y+z x}+\sqrt{z+x y} \geq \sqrt{x y z}+\sqrt{x}+\sqrt{y}+\sqrt{z}
$$
|
$$
\begin{aligned}
\sum_{\text {cyclic }} \sqrt{x+y z} & =\sqrt{x y z} \sum_{\text {cyclic }} \sqrt{\frac{1}{x}+\frac{1}{y z}} \\
& =\sqrt{x y z} \sum_{\text {cyclic }} \sqrt{\frac{1}{x}\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)+\frac{1}{y z}} \quad[1 \text { mark. }] \\
& =\sqrt{x y z} \sum_{\text {cyclic }} \sqrt{\left(\frac{1}{x}+\frac{1}{y}\right)\left(\frac{1}{x}+\frac{1}{z}\right)} \quad[1 \text { mark.] }
\end{aligned}
$$
$$
\begin{aligned}
& =\sqrt{x y z} \sum_{\text {cyclic }} \sqrt{\left(\frac{1}{x}+\frac{1}{\sqrt{y z}}\right)^{2}+\frac{(\sqrt{y}-\sqrt{z})^{2}}{x y z}} \quad[2 \text { marks. }] \\
& \geq \sqrt{x y z} \sum_{\text {cyclic }}\left(\frac{1}{x}+\frac{1}{\sqrt{y z}}\right) \quad[1 \text { mark. }] \\
& =\sqrt{x y z}\left(1+\sum_{\text {cyclic }} \frac{1}{\sqrt{y z}}\right) \quad[1 \text { mark. }] \\
& =\sqrt{x y z}+\sum_{\text {cyclic }} \sqrt{x} \quad[1 \text { mark. }]
\end{aligned}
$$
Note. It is easy to check that equality holds if and only if $x=y=z=3$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $x, y, z$ be positive numbers such that
$$
\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1
$$
Show that
$$
\sqrt{x+y z}+\sqrt{y+z x}+\sqrt{z+x y} \geq \sqrt{x y z}+\sqrt{x}+\sqrt{y}+\sqrt{z}
$$
|
$$
\begin{aligned}
\sum_{\text {cyclic }} \sqrt{x+y z} & =\sqrt{x y z} \sum_{\text {cyclic }} \sqrt{\frac{1}{x}+\frac{1}{y z}} \\
& =\sqrt{x y z} \sum_{\text {cyclic }} \sqrt{\frac{1}{x}\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)+\frac{1}{y z}} \quad[1 \text { mark. }] \\
& =\sqrt{x y z} \sum_{\text {cyclic }} \sqrt{\left(\frac{1}{x}+\frac{1}{y}\right)\left(\frac{1}{x}+\frac{1}{z}\right)} \quad[1 \text { mark.] }
\end{aligned}
$$
$$
\begin{aligned}
& =\sqrt{x y z} \sum_{\text {cyclic }} \sqrt{\left(\frac{1}{x}+\frac{1}{\sqrt{y z}}\right)^{2}+\frac{(\sqrt{y}-\sqrt{z})^{2}}{x y z}} \quad[2 \text { marks. }] \\
& \geq \sqrt{x y z} \sum_{\text {cyclic }}\left(\frac{1}{x}+\frac{1}{\sqrt{y z}}\right) \quad[1 \text { mark. }] \\
& =\sqrt{x y z}\left(1+\sum_{\text {cyclic }} \frac{1}{\sqrt{y z}}\right) \quad[1 \text { mark. }] \\
& =\sqrt{x y z}+\sum_{\text {cyclic }} \sqrt{x} \quad[1 \text { mark. }]
\end{aligned}
$$
Note. It is easy to check that equality holds if and only if $x=y=z=3$.
|
{
"resource_path": "APMO/segmented/en-apmo2002_sol.jsonl",
"problem_match": "\n4. ",
"solution_match": "\nSolution 1."
}
|
2ce20b58-70b3-5744-a593-c218e443a610
| 607,117
|
Let $x, y, z$ be positive numbers such that
$$
\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1
$$
Show that
$$
\sqrt{x+y z}+\sqrt{y+z x}+\sqrt{z+x y} \geq \sqrt{x y z}+\sqrt{x}+\sqrt{y}+\sqrt{z}
$$
|
Squaring both sides of the given inequality, we obtain
$$
\begin{aligned}
& \sum_{\text {cyclic }} x+\sum_{\text {cyclic }} y z+2 \sum_{\text {cyclic }} \sqrt{x+y z} \sqrt{y+z x} \\
& \quad \geq x y z+2 \sqrt{x y z} \sum_{\text {cyclic }} \sqrt{x}+\sum_{\text {cyclic }} x+2 \sum_{\text {cyclic }} \sqrt{x y} \quad \text { [1 mark.] }
\end{aligned}
$$
It follows from the given condition $\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1$ that $x y z=\sum_{\text {cyclic }} x y$. Therefore, the given inequality is equivalent to
$$
\sum_{\text {cyclic }} \sqrt{x+y z} \sqrt{y+z x} \geq \sqrt{x y z} \sum_{\text {cyclic }} \sqrt{x}+\sum_{\text {cyclic }} \sqrt{x y} . \quad[2 \text { marks.] }
$$
Using the Cauchy-Schwarz inequality [or just $x^{2}+y^{2} \geq 2 x y$ ], we see that
$$
(x+y z)(y+z x) \geq\left(\sqrt{x y}+\sqrt{x y z^{2}}\right)^{2}, \quad[1 \text { mark. }]
$$
or
$$
\sqrt{x+y z} \sqrt{y+z x} \geq \sqrt{x y}+\sqrt{z} \sqrt{x y z} . \quad[1 \text { mark. }]
$$
Taking the cyclic sum of this inequality over $x, y$ and $z$, we get the desired inequality. [2 marks.]
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $x, y, z$ be positive numbers such that
$$
\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1
$$
Show that
$$
\sqrt{x+y z}+\sqrt{y+z x}+\sqrt{z+x y} \geq \sqrt{x y z}+\sqrt{x}+\sqrt{y}+\sqrt{z}
$$
|
Squaring both sides of the given inequality, we obtain
$$
\begin{aligned}
& \sum_{\text {cyclic }} x+\sum_{\text {cyclic }} y z+2 \sum_{\text {cyclic }} \sqrt{x+y z} \sqrt{y+z x} \\
& \quad \geq x y z+2 \sqrt{x y z} \sum_{\text {cyclic }} \sqrt{x}+\sum_{\text {cyclic }} x+2 \sum_{\text {cyclic }} \sqrt{x y} \quad \text { [1 mark.] }
\end{aligned}
$$
It follows from the given condition $\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1$ that $x y z=\sum_{\text {cyclic }} x y$. Therefore, the given inequality is equivalent to
$$
\sum_{\text {cyclic }} \sqrt{x+y z} \sqrt{y+z x} \geq \sqrt{x y z} \sum_{\text {cyclic }} \sqrt{x}+\sum_{\text {cyclic }} \sqrt{x y} . \quad[2 \text { marks.] }
$$
Using the Cauchy-Schwarz inequality [or just $x^{2}+y^{2} \geq 2 x y$ ], we see that
$$
(x+y z)(y+z x) \geq\left(\sqrt{x y}+\sqrt{x y z^{2}}\right)^{2}, \quad[1 \text { mark. }]
$$
or
$$
\sqrt{x+y z} \sqrt{y+z x} \geq \sqrt{x y}+\sqrt{z} \sqrt{x y z} . \quad[1 \text { mark. }]
$$
Taking the cyclic sum of this inequality over $x, y$ and $z$, we get the desired inequality. [2 marks.]
|
{
"resource_path": "APMO/segmented/en-apmo2002_sol.jsonl",
"problem_match": "\n4. ",
"solution_match": "\nSolution 2."
}
|
2ce20b58-70b3-5744-a593-c218e443a610
| 607,117
|
Let $x, y, z$ be positive numbers such that
$$
\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1
$$
Show that
$$
\sqrt{x+y z}+\sqrt{y+z x}+\sqrt{z+x y} \geq \sqrt{x y z}+\sqrt{x}+\sqrt{y}+\sqrt{z}
$$
|
This is another way of presenting the idea in the first solution.
Using the condition $\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1$ and the AM-GM inequality, we have
$$
\begin{aligned}
x+y z-\left(\sqrt{\frac{y z}{x}}+\sqrt{x}\right)^{2} & =y z\left(1-\frac{1}{x}\right)-2 \sqrt{y z} \\
& =y z\left(\frac{1}{y}+\frac{1}{z}\right)-2 \sqrt{y z}=y+z-2 \sqrt{y z} \geq 0
\end{aligned}
$$
which gives
$$
\sqrt{x+y z} \geq \sqrt{\frac{y z}{x}}+\sqrt{x} . \quad[3 \text { marks. }]
$$
Similarly, we have
$$
\sqrt{y+z x} \geq \sqrt{\frac{z x}{y}}+\sqrt{y} \text { and } \sqrt{z+x y} \geq \sqrt{\frac{x y}{z}}+\sqrt{z}
$$
Addition yields
$$
\sqrt{x+y z}+\sqrt{y+z x}+\sqrt{z+x y} \geq \sqrt{\frac{y z}{x}}+\sqrt{\frac{z x}{y}}+\sqrt{\frac{x y}{z}}+\sqrt{x}+\sqrt{y}+\sqrt{z}
$$
[2 marks.] Using the condition $\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1$ again, we have
$$
\sqrt{\frac{y z}{x}}+\sqrt{\frac{z x}{y}}+\sqrt{\frac{x y}{z}}=\sqrt{x y z}\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)=\sqrt{x y z}, \quad[1 \text { mark. }]
$$
and thus
$$
\sqrt{x+y z}+\sqrt{y+z x}+\sqrt{z+x y} \geq \sqrt{x y z}+\sqrt{x}+\sqrt{y}+\sqrt{z} . \quad[1 \text { mark. }]
$$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $x, y, z$ be positive numbers such that
$$
\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1
$$
Show that
$$
\sqrt{x+y z}+\sqrt{y+z x}+\sqrt{z+x y} \geq \sqrt{x y z}+\sqrt{x}+\sqrt{y}+\sqrt{z}
$$
|
This is another way of presenting the idea in the first solution.
Using the condition $\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1$ and the AM-GM inequality, we have
$$
\begin{aligned}
x+y z-\left(\sqrt{\frac{y z}{x}}+\sqrt{x}\right)^{2} & =y z\left(1-\frac{1}{x}\right)-2 \sqrt{y z} \\
& =y z\left(\frac{1}{y}+\frac{1}{z}\right)-2 \sqrt{y z}=y+z-2 \sqrt{y z} \geq 0
\end{aligned}
$$
which gives
$$
\sqrt{x+y z} \geq \sqrt{\frac{y z}{x}}+\sqrt{x} . \quad[3 \text { marks. }]
$$
Similarly, we have
$$
\sqrt{y+z x} \geq \sqrt{\frac{z x}{y}}+\sqrt{y} \text { and } \sqrt{z+x y} \geq \sqrt{\frac{x y}{z}}+\sqrt{z}
$$
Addition yields
$$
\sqrt{x+y z}+\sqrt{y+z x}+\sqrt{z+x y} \geq \sqrt{\frac{y z}{x}}+\sqrt{\frac{z x}{y}}+\sqrt{\frac{x y}{z}}+\sqrt{x}+\sqrt{y}+\sqrt{z}
$$
[2 marks.] Using the condition $\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1$ again, we have
$$
\sqrt{\frac{y z}{x}}+\sqrt{\frac{z x}{y}}+\sqrt{\frac{x y}{z}}=\sqrt{x y z}\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)=\sqrt{x y z}, \quad[1 \text { mark. }]
$$
and thus
$$
\sqrt{x+y z}+\sqrt{y+z x}+\sqrt{z+x y} \geq \sqrt{x y z}+\sqrt{x}+\sqrt{y}+\sqrt{z} . \quad[1 \text { mark. }]
$$
|
{
"resource_path": "APMO/segmented/en-apmo2002_sol.jsonl",
"problem_match": "\n4. ",
"solution_match": "\nSolution 3."
}
|
2ce20b58-70b3-5744-a593-c218e443a610
| 607,117
|
Let $x, y, z$ be positive numbers such that
$$
\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1
$$
Show that
$$
\sqrt{x+y z}+\sqrt{y+z x}+\sqrt{z+x y} \geq \sqrt{x y z}+\sqrt{x}+\sqrt{y}+\sqrt{z}
$$
|
This is also another way of presenting the idea in the first solution.
We make the substitution $a=\frac{1}{x}, b=\frac{1}{y}, c=\frac{1}{z}$. Then it is enough to show that
$$
\sqrt{\frac{1}{a}+\frac{1}{b c}}+\sqrt{\frac{1}{b}+\frac{1}{c a}}+\sqrt{\frac{1}{c}+\frac{1}{a b}} \geq \sqrt{\frac{1}{a b c}}+\sqrt{\frac{1}{a}}+\sqrt{\frac{1}{b}}+\sqrt{\frac{1}{c}},
$$
where $a+b+c=1$. Multiplying this inequality by $\sqrt{a b c}$, we find that it can be written
$$
\sqrt{a+b c}+\sqrt{b+c a}+\sqrt{c+a b} \geq 1+\sqrt{b c}+\sqrt{c a}+\sqrt{a b} . \quad[1 \text { mark. }]
$$
This is equivalent to
$$
\begin{aligned}
& \sqrt{a(a+b+c)+b c}+\sqrt{b(a+b+c)+c a}+\sqrt{c(a+b+c)+a b} \\
& \geq a+b+c+\sqrt{b c}+\sqrt{c a}+\sqrt{a b}, \quad[1 \text { mark. }]
\end{aligned}
$$
which in turn is equivalent to
$$
\sqrt{(a+b)(a+c)}+\sqrt{(b+c)(b+a)}+\sqrt{(c+a)(c+b)} \geq a+b+c+\sqrt{b c}+\sqrt{c a}+\sqrt{a b}
$$
[1 mark.] (This is a homogeneous version of the original inequality.) By the Cauchy-Schwarz inequality (or since $b+c \geq 2 \sqrt{b c}$ ), we have
$$
\left[(\sqrt{a})^{2}+(\sqrt{b})^{2}\right]\left[(\sqrt{a})^{2}+(\sqrt{c})^{2}\right] \geq(\sqrt{a} \sqrt{a}+\sqrt{b} \sqrt{c})^{2}
$$
or
$$
\sqrt{(a+b)(a+c)} \geq a+\sqrt{b c} . \quad[2 \text { marks. }]
$$
Taking the cyclic sum of this inequality over $a, b, c$, we get the desired inequality. [2 marks.]
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $x, y, z$ be positive numbers such that
$$
\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1
$$
Show that
$$
\sqrt{x+y z}+\sqrt{y+z x}+\sqrt{z+x y} \geq \sqrt{x y z}+\sqrt{x}+\sqrt{y}+\sqrt{z}
$$
|
This is also another way of presenting the idea in the first solution.
We make the substitution $a=\frac{1}{x}, b=\frac{1}{y}, c=\frac{1}{z}$. Then it is enough to show that
$$
\sqrt{\frac{1}{a}+\frac{1}{b c}}+\sqrt{\frac{1}{b}+\frac{1}{c a}}+\sqrt{\frac{1}{c}+\frac{1}{a b}} \geq \sqrt{\frac{1}{a b c}}+\sqrt{\frac{1}{a}}+\sqrt{\frac{1}{b}}+\sqrt{\frac{1}{c}},
$$
where $a+b+c=1$. Multiplying this inequality by $\sqrt{a b c}$, we find that it can be written
$$
\sqrt{a+b c}+\sqrt{b+c a}+\sqrt{c+a b} \geq 1+\sqrt{b c}+\sqrt{c a}+\sqrt{a b} . \quad[1 \text { mark. }]
$$
This is equivalent to
$$
\begin{aligned}
& \sqrt{a(a+b+c)+b c}+\sqrt{b(a+b+c)+c a}+\sqrt{c(a+b+c)+a b} \\
& \geq a+b+c+\sqrt{b c}+\sqrt{c a}+\sqrt{a b}, \quad[1 \text { mark. }]
\end{aligned}
$$
which in turn is equivalent to
$$
\sqrt{(a+b)(a+c)}+\sqrt{(b+c)(b+a)}+\sqrt{(c+a)(c+b)} \geq a+b+c+\sqrt{b c}+\sqrt{c a}+\sqrt{a b}
$$
[1 mark.] (This is a homogeneous version of the original inequality.) By the Cauchy-Schwarz inequality (or since $b+c \geq 2 \sqrt{b c}$ ), we have
$$
\left[(\sqrt{a})^{2}+(\sqrt{b})^{2}\right]\left[(\sqrt{a})^{2}+(\sqrt{c})^{2}\right] \geq(\sqrt{a} \sqrt{a}+\sqrt{b} \sqrt{c})^{2}
$$
or
$$
\sqrt{(a+b)(a+c)} \geq a+\sqrt{b c} . \quad[2 \text { marks. }]
$$
Taking the cyclic sum of this inequality over $a, b, c$, we get the desired inequality. [2 marks.]
|
{
"resource_path": "APMO/segmented/en-apmo2002_sol.jsonl",
"problem_match": "\n4. ",
"solution_match": "# Solution 4."
}
|
2ce20b58-70b3-5744-a593-c218e443a610
| 607,117
|
Let R denote the set of all real numbers. Find all functions $f$ from R to R satisfying:
(i) there are only finitely many $s$ in R such that $f(s)=0$, and
(ii) $f\left(x^{4}+y\right)=x^{3} f(x)+f(f(y))$ for all $x, y$ in $\mathbf{R}$.
|
The only such function is the identity function on $R$.
Setting $(x, y)=(1,0)$ in the given functional equation (ii), we have $f(f(0))=0$. Setting $x=0$ in (ii), we find
$$
f(y)=f(f(y))
$$
[1 mark.] and thus $f(0)=f(f(0))=0$ [1 mark.]. It follows from (ii) that $f\left(x^{4}+y\right)=$ $x^{3} f(x)+f(y)$ for all $x, y \in \mathbf{R}$. Set $y=0$ to obtain
$$
f\left(x^{4}\right)=x^{3} f(x)
$$
for all $x \in \mathrm{R}$, and so
$$
f\left(x^{4}+y\right)=f\left(x^{4}\right)+f(y)
$$
for all $x, y \in \mathbf{R}$. The functional equation (3) suggests that $f$ is additive, that is, $f(a+b)=$ $f(a)+f(b)$ for all $a, b \in \mathbf{R}$. [1 mark.] We now show this.
First assume that $a \geq 0$ and $b \in R$. It follows from (3) that
$$
f(a+b)=f\left(\left(a^{1 / 4}\right)^{4}+b\right)=f\left(\left(a^{1 / 4}\right)^{4}\right)+f(b)=f(a)+f(b)
$$
We next note that $f$ is an odd function, since from (2)
$$
f(-x)=\frac{f\left(x^{4}\right)}{(-x)^{3}}=\frac{f\left(x^{4}\right)}{-x^{3}}=-f(x), \quad x \neq 0
$$
Since $f$ is odd, we have that, for $a<0$ and $b \in R$,
$$
\begin{aligned}
f(a+b) & =-f((-a)+(-b))=-(f(-a)+f(-b)) \\
& =-(-f(a)-f(b))=f(a)+f(b)
\end{aligned}
$$
Therefore, we conclude that $f(a+b)=f(a)+f(b)$ for all $a, b \in R$. [2 mers.].]
We now show that $\{s \in \mathrm{R} \mid f(s)=0\}=\{0\}$. Recall that $f(0)=0$. Assume that there is a nonzero $h \in \mathrm{R}$ such that $f(h)=0$. Then, using the fact that $f$ is additive, we inductively have $f(n h)=0$ or $n h \in\{s \in R \mid f(s)=0\}$ for all $n \in \mathbf{N}$. However, this is a contradiction to the given condition (i). [1 mark.]
It's now easy to check that $f$ is one-to-one. Assume that $f(a)=f^{\prime}(b)$ for some $a, b \in \mathbb{P}$. Then, we have $f(b)=f(a)=f(a-b)+f(b)$ or $f(a-b)=0$. This implies that $a-b \in\{s \in$ $\mathbf{R} \mid f(s)=0\}=\{0\}$ or $a=b$, as desired. From (1) and the fact that $f$ is one-to-one, we deduce that $f(x)=x$ for all $x \in \mathbf{R}$. [1 mark.] This completes the proof.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let R denote the set of all real numbers. Find all functions $f$ from R to R satisfying:
(i) there are only finitely many $s$ in R such that $f(s)=0$, and
(ii) $f\left(x^{4}+y\right)=x^{3} f(x)+f(f(y))$ for all $x, y$ in $\mathbf{R}$.
|
The only such function is the identity function on $R$.
Setting $(x, y)=(1,0)$ in the given functional equation (ii), we have $f(f(0))=0$. Setting $x=0$ in (ii), we find
$$
f(y)=f(f(y))
$$
[1 mark.] and thus $f(0)=f(f(0))=0$ [1 mark.]. It follows from (ii) that $f\left(x^{4}+y\right)=$ $x^{3} f(x)+f(y)$ for all $x, y \in \mathbf{R}$. Set $y=0$ to obtain
$$
f\left(x^{4}\right)=x^{3} f(x)
$$
for all $x \in \mathrm{R}$, and so
$$
f\left(x^{4}+y\right)=f\left(x^{4}\right)+f(y)
$$
for all $x, y \in \mathbf{R}$. The functional equation (3) suggests that $f$ is additive, that is, $f(a+b)=$ $f(a)+f(b)$ for all $a, b \in \mathbf{R}$. [1 mark.] We now show this.
First assume that $a \geq 0$ and $b \in R$. It follows from (3) that
$$
f(a+b)=f\left(\left(a^{1 / 4}\right)^{4}+b\right)=f\left(\left(a^{1 / 4}\right)^{4}\right)+f(b)=f(a)+f(b)
$$
We next note that $f$ is an odd function, since from (2)
$$
f(-x)=\frac{f\left(x^{4}\right)}{(-x)^{3}}=\frac{f\left(x^{4}\right)}{-x^{3}}=-f(x), \quad x \neq 0
$$
Since $f$ is odd, we have that, for $a<0$ and $b \in R$,
$$
\begin{aligned}
f(a+b) & =-f((-a)+(-b))=-(f(-a)+f(-b)) \\
& =-(-f(a)-f(b))=f(a)+f(b)
\end{aligned}
$$
Therefore, we conclude that $f(a+b)=f(a)+f(b)$ for all $a, b \in R$. [2 mers.].]
We now show that $\{s \in \mathrm{R} \mid f(s)=0\}=\{0\}$. Recall that $f(0)=0$. Assume that there is a nonzero $h \in \mathrm{R}$ such that $f(h)=0$. Then, using the fact that $f$ is additive, we inductively have $f(n h)=0$ or $n h \in\{s \in R \mid f(s)=0\}$ for all $n \in \mathbf{N}$. However, this is a contradiction to the given condition (i). [1 mark.]
It's now easy to check that $f$ is one-to-one. Assume that $f(a)=f^{\prime}(b)$ for some $a, b \in \mathbb{P}$. Then, we have $f(b)=f(a)=f(a-b)+f(b)$ or $f(a-b)=0$. This implies that $a-b \in\{s \in$ $\mathbf{R} \mid f(s)=0\}=\{0\}$ or $a=b$, as desired. From (1) and the fact that $f$ is one-to-one, we deduce that $f(x)=x$ for all $x \in \mathbf{R}$. [1 mark.] This completes the proof.
|
{
"resource_path": "APMO/segmented/en-apmo2002_sol.jsonl",
"problem_match": "\n5. ",
"solution_match": "# Solution 1."
}
|
293d8275-a3b7-56e6-8a79-708458aeba3a
| 607,118
|
Let R denote the set of all real numbers. Find all functions $f$ from R to R satisfying:
(i) there are only finitely many $s$ in R such that $f(s)=0$, and
(ii) $f\left(x^{4}+y\right)=x^{3} f(x)+f(f(y))$ for all $x, y$ in $\mathbf{R}$.
|
Again, the only such function is the identity function on R .
As in Solution 1, we first show that $f(f(y))=f(y), f(0)=0$, and $f\left(x^{4}\right)=x^{3} f(x)$. [2 marks.] From the latter follows
$$
f(x)=0 \Longrightarrow f\left(x^{4}\right)=0
$$
and from condition (i) we get that $f(x)=0$ only possibly for $x \in\{0,1,-1\}$. [1 mark.]
Next we prove
$$
f(a)=b \Longrightarrow f(\sqrt[4]{|a-b|})=0
$$
This is clear if $a=b$. If $a>b$ then
$$
\begin{aligned}
f(a) & =f((a-b)+b)=(a-b)^{3 / 4} f(\sqrt[4]{a-b})+f(f(b)) \\
& =(a-b)^{3 / 4} f(\sqrt[4]{a-b})+f(b) \\
& =(a-b)^{3 / 4} f(\sqrt[4]{a-b})+f(f(a)) \\
& =(a-b)^{3 / 4} f(\sqrt[4]{a-b})+f(a),
\end{aligned}
$$
so $(a-b)^{3 / 4} f(\sqrt[4]{a-b})=0$ which means $f(\sqrt[4]{|a-b|})=0$. If $a<b$ we get similarly
$$
\begin{aligned}
f(b) & =f((b-a)+a)=(b-a)^{3 / 4} f(\sqrt[4]{b-a})+f(f(a)) \\
& =(b-a)^{3 / 4} f(\sqrt[4]{b-a})+f(b)
\end{aligned}
$$
and again $f(\sqrt[4]{|a-b|})=0$. [2 marks.]
Thus $f(a)=b \Longrightarrow|a-b| \in\{0,1\}$. Suppose that $f(x)=x+b$ for some $x$, where $|b|=1$. Then from $f\left(x^{4}\right)=x^{3} f(x)$ and $f\left(x^{4}\right)=x^{4}+a$ for some $|a| \leq 1$ we get $x^{3}=a / b$, so $|x| \leq 1$. Thus $f(x)=x$ for all $x$ except possibly $x= \pm 1$. [ 1 mark.] But for example,
$$
f(1)=f\left(2^{4}-15\right)=2^{3} f(2)+f(f(-15))=2^{3} \cdot 2-15=1
$$
and
$$
f(-1)=f\left(2^{4}-17\right)=2^{3} f(2)+f(f(-17))=2^{3} \cdot 2-17=-1
$$
[1 mark.] This finishes the proof.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let R denote the set of all real numbers. Find all functions $f$ from R to R satisfying:
(i) there are only finitely many $s$ in R such that $f(s)=0$, and
(ii) $f\left(x^{4}+y\right)=x^{3} f(x)+f(f(y))$ for all $x, y$ in $\mathbf{R}$.
|
Again, the only such function is the identity function on R .
As in Solution 1, we first show that $f(f(y))=f(y), f(0)=0$, and $f\left(x^{4}\right)=x^{3} f(x)$. [2 marks.] From the latter follows
$$
f(x)=0 \Longrightarrow f\left(x^{4}\right)=0
$$
and from condition (i) we get that $f(x)=0$ only possibly for $x \in\{0,1,-1\}$. [1 mark.]
Next we prove
$$
f(a)=b \Longrightarrow f(\sqrt[4]{|a-b|})=0
$$
This is clear if $a=b$. If $a>b$ then
$$
\begin{aligned}
f(a) & =f((a-b)+b)=(a-b)^{3 / 4} f(\sqrt[4]{a-b})+f(f(b)) \\
& =(a-b)^{3 / 4} f(\sqrt[4]{a-b})+f(b) \\
& =(a-b)^{3 / 4} f(\sqrt[4]{a-b})+f(f(a)) \\
& =(a-b)^{3 / 4} f(\sqrt[4]{a-b})+f(a),
\end{aligned}
$$
so $(a-b)^{3 / 4} f(\sqrt[4]{a-b})=0$ which means $f(\sqrt[4]{|a-b|})=0$. If $a<b$ we get similarly
$$
\begin{aligned}
f(b) & =f((b-a)+a)=(b-a)^{3 / 4} f(\sqrt[4]{b-a})+f(f(a)) \\
& =(b-a)^{3 / 4} f(\sqrt[4]{b-a})+f(b)
\end{aligned}
$$
and again $f(\sqrt[4]{|a-b|})=0$. [2 marks.]
Thus $f(a)=b \Longrightarrow|a-b| \in\{0,1\}$. Suppose that $f(x)=x+b$ for some $x$, where $|b|=1$. Then from $f\left(x^{4}\right)=x^{3} f(x)$ and $f\left(x^{4}\right)=x^{4}+a$ for some $|a| \leq 1$ we get $x^{3}=a / b$, so $|x| \leq 1$. Thus $f(x)=x$ for all $x$ except possibly $x= \pm 1$. [ 1 mark.] But for example,
$$
f(1)=f\left(2^{4}-15\right)=2^{3} f(2)+f(f(-15))=2^{3} \cdot 2-15=1
$$
and
$$
f(-1)=f\left(2^{4}-17\right)=2^{3} f(2)+f(f(-17))=2^{3} \cdot 2-17=-1
$$
[1 mark.] This finishes the proof.
|
{
"resource_path": "APMO/segmented/en-apmo2002_sol.jsonl",
"problem_match": "\n5. ",
"solution_match": "# Solution 2."
}
|
293d8275-a3b7-56e6-8a79-708458aeba3a
| 607,118
|
Let $a, b, c, d, e, f$ be real numbers such that the polynomial
$$
p(x)=x^{8}-4 x^{7}+7 x^{6}+a x^{5}+b x^{4}+c x^{3}+d x^{2}+e x+f
$$
factorises into eight linear factors $x-x_{i}$, with $x_{i}>0$ for $i=1,2, \ldots, 8$. Determine all possible values of $f$.
|
From
$$
x^{8}-4 x^{7}+7 x^{6}+a x^{5}+b x^{4}+c x^{3}+d x^{2}+e x+f=\left(x-x_{1}\right)\left(x-x_{2}\right) \ldots\left(x-x_{8}\right)
$$
we have
$$
\sum_{i=1}^{8} x_{i}=4 \quad \text { and } \quad \sum x_{i} x_{j}=7
$$
where the second sum is over all pairs $(i, j)$ of integers where $1 \leq i<j \leq 8$. Since this sum can also be written
$$
\frac{1}{2}\left[\left(\sum_{i=1}^{8} x_{i}\right)^{2}-\sum_{i=1}^{8} x_{i}^{2}\right]
$$
we get
$$
14=\left(\sum_{i=1}^{8} x_{i}\right)^{2}-\sum_{i=1}^{8} x_{i}^{2}=16-\sum_{i=1}^{8} x_{i}^{2}
$$
so
$$
\sum_{i=1}^{8} x_{i}^{2}=2 \quad \text { while } \quad \sum_{i=1}^{8} x_{i}=4 . \quad[3 \text { marks }]
$$
Now
$$
\sum_{i=1}^{8}\left(2 x_{i}-1\right)^{2}=4 \sum_{i=1}^{8} x_{i}^{2}-4 \sum_{i=1}^{8} x_{i}+8=4(2)-4(4)+8=0
$$
which forces $x_{i}=1 / 2$ for all $i$. [3 marks] Therefore
$$
f=\prod_{i=1}^{8} x_{i}=\left(\frac{1}{2}\right)^{8}=\frac{1}{256} . \quad[1 m x]
$$
Alternate solution: After obtaining (1) [3 marks], use Cauchy's inequality to get
$$
16=\left(x_{1} \cdot 1+x_{2} \cdot 1+\cdots+x_{8} \cdot 1\right)^{2} \leq\left(x_{1}^{2-}+x_{2}^{2}+\cdots+x_{8}^{2}\right)\left(1^{2}+1^{2}+\cdots+1^{2}\right)=8 \cdot 2=16
$$
or the power mean inequality to get
$$
\frac{1}{2}=\frac{1}{8} \sum_{i=1}^{8} x_{i} \leq\left(\frac{1}{8} \sum_{i=1}^{8} x_{i}^{2}\right)^{1 / 2}=\frac{1}{2} . \quad[2 \text { marks }]
$$
Either way, equality must hold, which can only happen if all the terms $x_{i}$ are equal, that is, if $x_{i}=1 / 2$ for all $i$. [1 mark] Thus $f=1 / 256$ as above. [ 1 mark]
|
\frac{1}{256}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $a, b, c, d, e, f$ be real numbers such that the polynomial
$$
p(x)=x^{8}-4 x^{7}+7 x^{6}+a x^{5}+b x^{4}+c x^{3}+d x^{2}+e x+f
$$
factorises into eight linear factors $x-x_{i}$, with $x_{i}>0$ for $i=1,2, \ldots, 8$. Determine all possible values of $f$.
|
From
$$
x^{8}-4 x^{7}+7 x^{6}+a x^{5}+b x^{4}+c x^{3}+d x^{2}+e x+f=\left(x-x_{1}\right)\left(x-x_{2}\right) \ldots\left(x-x_{8}\right)
$$
we have
$$
\sum_{i=1}^{8} x_{i}=4 \quad \text { and } \quad \sum x_{i} x_{j}=7
$$
where the second sum is over all pairs $(i, j)$ of integers where $1 \leq i<j \leq 8$. Since this sum can also be written
$$
\frac{1}{2}\left[\left(\sum_{i=1}^{8} x_{i}\right)^{2}-\sum_{i=1}^{8} x_{i}^{2}\right]
$$
we get
$$
14=\left(\sum_{i=1}^{8} x_{i}\right)^{2}-\sum_{i=1}^{8} x_{i}^{2}=16-\sum_{i=1}^{8} x_{i}^{2}
$$
so
$$
\sum_{i=1}^{8} x_{i}^{2}=2 \quad \text { while } \quad \sum_{i=1}^{8} x_{i}=4 . \quad[3 \text { marks }]
$$
Now
$$
\sum_{i=1}^{8}\left(2 x_{i}-1\right)^{2}=4 \sum_{i=1}^{8} x_{i}^{2}-4 \sum_{i=1}^{8} x_{i}+8=4(2)-4(4)+8=0
$$
which forces $x_{i}=1 / 2$ for all $i$. [3 marks] Therefore
$$
f=\prod_{i=1}^{8} x_{i}=\left(\frac{1}{2}\right)^{8}=\frac{1}{256} . \quad[1 m x]
$$
Alternate solution: After obtaining (1) [3 marks], use Cauchy's inequality to get
$$
16=\left(x_{1} \cdot 1+x_{2} \cdot 1+\cdots+x_{8} \cdot 1\right)^{2} \leq\left(x_{1}^{2-}+x_{2}^{2}+\cdots+x_{8}^{2}\right)\left(1^{2}+1^{2}+\cdots+1^{2}\right)=8 \cdot 2=16
$$
or the power mean inequality to get
$$
\frac{1}{2}=\frac{1}{8} \sum_{i=1}^{8} x_{i} \leq\left(\frac{1}{8} \sum_{i=1}^{8} x_{i}^{2}\right)^{1 / 2}=\frac{1}{2} . \quad[2 \text { marks }]
$$
Either way, equality must hold, which can only happen if all the terms $x_{i}$ are equal, that is, if $x_{i}=1 / 2$ for all $i$. [1 mark] Thus $f=1 / 256$ as above. [ 1 mark]
|
{
"resource_path": "APMO/segmented/en-apmo2003_sol.jsonl",
"problem_match": "\n1. ",
"solution_match": "# Solution."
}
|
c13852dc-b4a2-516c-ba98-28de916b4f95
| 607,119
|
Suppose $A B C D$ is a square piece of cardboard with side length $a$. On a plane are two parallel lines $\ell_{1}$ and $\ell_{2}$, which are also $a$ units apart. The square $A B C D$ is placed on the plane so that sides $A B$ and $A D$ intersect $\ell_{1}$ at $E$ and $F$ respectively. Also, sides $C B$ and $C D$ intersect $\ell_{2}$ at $G$ and $H$ respectively. Let the perimeters of $\triangle A E F$ and $\triangle C G H$ be $m_{1}$ and $m_{2}$ respectively. Prove that no matter how the square was placed, $m_{1}+m_{2}$ remains constant.
|
Let $E H$ intersect $F G$ at $O$. The distance from $G$ to line $F D$ and line $E F$ are both $a$. So $F G$ bisects $\angle E F D$. Similarly, $E H$ bisects $\angle B E F$. So $O$ is an excentre of $\triangle A E F$. Similarly, $O$ is an excentre of $\triangle C G H$. [2 marks] Construct these excircles with centre $O$. Let $M, N, P, Q$ be on sides $A B, B C, C D, D A$ respectively, where these excircles touch the square. Then $O M \perp A B, O N \perp B C, O P \perp C D$, and $O Q \perp D A$. Since $A B \| C D$ and $A D \| B C, M, O, P$ are collinear and $N, O, Q$ are collinear. Now $M P=N Q=a$. [2 marks] Using the fact that the two tangents from a point to a circle have the same length, we get $E F=E M+F Q$ and $G H=G N+H P$. [1 mark] Then
$$
m_{1}=A E+A F+E F=A E+A F+(E M+F Q)=A M+A Q=O Q+O M
$$
and
$$
m_{2}=C G+C H+G H=C G+C H+(G N+H P)=C N+C P=O P+O N . \quad[1 \text { mark }]
$$
Therefore
$$
m_{1}+m_{2}=(O Q+O M)+(O P+O N)=M P+N Q=2 a . \quad[1 \mathrm{mark}]
$$
|
2a
|
Yes
|
Yes
|
proof
|
Geometry
|
Suppose $A B C D$ is a square piece of cardboard with side length $a$. On a plane are two parallel lines $\ell_{1}$ and $\ell_{2}$, which are also $a$ units apart. The square $A B C D$ is placed on the plane so that sides $A B$ and $A D$ intersect $\ell_{1}$ at $E$ and $F$ respectively. Also, sides $C B$ and $C D$ intersect $\ell_{2}$ at $G$ and $H$ respectively. Let the perimeters of $\triangle A E F$ and $\triangle C G H$ be $m_{1}$ and $m_{2}$ respectively. Prove that no matter how the square was placed, $m_{1}+m_{2}$ remains constant.
|
Let $E H$ intersect $F G$ at $O$. The distance from $G$ to line $F D$ and line $E F$ are both $a$. So $F G$ bisects $\angle E F D$. Similarly, $E H$ bisects $\angle B E F$. So $O$ is an excentre of $\triangle A E F$. Similarly, $O$ is an excentre of $\triangle C G H$. [2 marks] Construct these excircles with centre $O$. Let $M, N, P, Q$ be on sides $A B, B C, C D, D A$ respectively, where these excircles touch the square. Then $O M \perp A B, O N \perp B C, O P \perp C D$, and $O Q \perp D A$. Since $A B \| C D$ and $A D \| B C, M, O, P$ are collinear and $N, O, Q$ are collinear. Now $M P=N Q=a$. [2 marks] Using the fact that the two tangents from a point to a circle have the same length, we get $E F=E M+F Q$ and $G H=G N+H P$. [1 mark] Then
$$
m_{1}=A E+A F+E F=A E+A F+(E M+F Q)=A M+A Q=O Q+O M
$$
and
$$
m_{2}=C G+C H+G H=C G+C H+(G N+H P)=C N+C P=O P+O N . \quad[1 \text { mark }]
$$
Therefore
$$
m_{1}+m_{2}=(O Q+O M)+(O P+O N)=M P+N Q=2 a . \quad[1 \mathrm{mark}]
$$
|
{
"resource_path": "APMO/segmented/en-apmo2003_sol.jsonl",
"problem_match": "\n2. ",
"solution_match": "\nSolution 1."
}
|
7f6794c9-bcf3-597c-a014-c2208022ac08
| 607,120
|
Suppose $A B C D$ is a square piece of cardboard with side length $a$. On a plane are two parallel lines $\ell_{1}$ and $\ell_{2}$, which are also $a$ units apart. The square $A B C D$ is placed on the plane so that sides $A B$ and $A D$ intersect $\ell_{1}$ at $E$ and $F$ respectively. Also, sides $C B$ and $C D$ intersect $\ell_{2}$ at $G$ and $H$ respectively. Let the perimeters of $\triangle A E F$ and $\triangle C G H$ be $m_{1}$ and $m_{2}$ respectively. Prove that no matter how the square was placed, $m_{1}+m_{2}$ remains constant.
|
Extend $A B$ to $I$ and $D C$ to $J$ so that $A E=B I=C J$. Let $\ell_{2}$ intersect $I J$ at $M$, and let $K$ lie on $I J$ so that $G K \perp I J$. Then, since $A E=G K, \triangle A E F$ and $\triangle K G M$ are congruent. [1 mark] Thus, since $G K=C J$ and $G C=K J$,
$$
m_{1}+m_{2}=\operatorname{perimeter}(K G M)+\operatorname{perimeter}(C G H)=\operatorname{perimeter}(H M J) . \quad[\mathbf{2} \text { marks }]
$$
Let $L$ lie on $C D$ so that $E L \perp C D$. Then a circle with centre $E$ and radius $a$ will touch $D C$ at $L, I J$ at $I$, and the interior of $H M$ at some point $N$, so
$$
\operatorname{perimeter}(H M J)=J H+(H N+N M)+J M=(J H+H L)+(M I+J M)=J L+I J=a+a=2 a
$$
[4 marks] Thus $m_{1}+m_{2}=2 a$.
|
2a
|
Yes
|
Yes
|
proof
|
Geometry
|
Suppose $A B C D$ is a square piece of cardboard with side length $a$. On a plane are two parallel lines $\ell_{1}$ and $\ell_{2}$, which are also $a$ units apart. The square $A B C D$ is placed on the plane so that sides $A B$ and $A D$ intersect $\ell_{1}$ at $E$ and $F$ respectively. Also, sides $C B$ and $C D$ intersect $\ell_{2}$ at $G$ and $H$ respectively. Let the perimeters of $\triangle A E F$ and $\triangle C G H$ be $m_{1}$ and $m_{2}$ respectively. Prove that no matter how the square was placed, $m_{1}+m_{2}$ remains constant.
|
Extend $A B$ to $I$ and $D C$ to $J$ so that $A E=B I=C J$. Let $\ell_{2}$ intersect $I J$ at $M$, and let $K$ lie on $I J$ so that $G K \perp I J$. Then, since $A E=G K, \triangle A E F$ and $\triangle K G M$ are congruent. [1 mark] Thus, since $G K=C J$ and $G C=K J$,
$$
m_{1}+m_{2}=\operatorname{perimeter}(K G M)+\operatorname{perimeter}(C G H)=\operatorname{perimeter}(H M J) . \quad[\mathbf{2} \text { marks }]
$$
Let $L$ lie on $C D$ so that $E L \perp C D$. Then a circle with centre $E$ and radius $a$ will touch $D C$ at $L, I J$ at $I$, and the interior of $H M$ at some point $N$, so
$$
\operatorname{perimeter}(H M J)=J H+(H N+N M)+J M=(J H+H L)+(M I+J M)=J L+I J=a+a=2 a
$$
[4 marks] Thus $m_{1}+m_{2}=2 a$.
|
{
"resource_path": "APMO/segmented/en-apmo2003_sol.jsonl",
"problem_match": "\n2. ",
"solution_match": "# Solution 2."
}
|
7f6794c9-bcf3-597c-a014-c2208022ac08
| 607,120
|
Suppose $A B C D$ is a square piece of cardboard with side length $a$. On a plane are two parallel lines $\ell_{1}$ and $\ell_{2}$, which are also $a$ units apart. The square $A B C D$ is placed on the plane so that sides $A B$ and $A D$ intersect $\ell_{1}$ at $E$ and $F$ respectively. Also, sides $C B$ and $C D$ intersect $\ell_{2}$ at $G$ and $H$ respectively. Let the perimeters of $\triangle A E F$ and $\triangle C G H$ be $m_{1}$ and $m_{2}$ respectively. Prove that no matter how the square was placed, $m_{1}+m_{2}$ remains constant.
|
Without loss of generality, assume the square has side $a=1$. Let $\theta$ be the acute angle between $\ell_{1}$ (or $\ell_{2}$ ) and the sides $A B$ and $C D$ of the square. Then, letting $E F=x$ and $G H=y$, we have
$$
E A=x \cos \theta, \quad A F=x \sin \theta, \quad C H=y \cos \theta, \quad C G=y \sin \theta
$$
Thus
$$
m_{1}+m_{2}=(x+y)(\sin \theta+\cos \theta+1) . \quad[2 \text { marks }]
$$
Draw lines parallel to $\ell_{1}, \ell_{2}$ through $A$ and $C$ respectively. The distance between these lines is $\sin \theta+\cos \theta$ [1 mark], as can be seen by drawing a mutual perpendicular to these lines through $B$, say. Also, the altitudes from $A$ to $E F$ and from $C$ to $G H$ have lengths $x \sin \theta \cos \theta$ and $y \sin \theta \cos \theta$ respectively [ 1 mark]. Therefore the distance between $\ell_{1}$ and $\ell_{2}$ must be
$$
(\sin \theta+\cos \theta)-x \sin \theta \cos \theta-y \sin \theta \cos \theta
$$
But we are given that this distance is $a=1$, so
$$
(x+y) \sin \theta \cos \theta+1=\sin \theta+\cos \theta
$$
or
$$
x+y=\frac{\sin \theta+\cos \theta-1}{\sin \theta \cos \theta} \cdot \quad[1 \text { mark }]
$$
Therefore, by (1),
$$
\begin{aligned}
m_{1}+m_{2} & =\frac{(\sin \theta+\cos \theta-1)(\sin \theta+\cos \theta+1)}{\sin \theta \cos \theta} \\
& =\frac{\left(\sin ^{2} \theta+\cos ^{2} \theta+2 \sin \theta \cos \theta\right)-1}{\sin \theta \cos \theta} \\
& =\frac{1+2 \sin \theta \cos \theta-1}{\sin \theta \cos \theta}=2 . \quad[2 \text { marks }]
\end{aligned}
$$
|
2
|
Yes
|
Yes
|
proof
|
Geometry
|
Suppose $A B C D$ is a square piece of cardboard with side length $a$. On a plane are two parallel lines $\ell_{1}$ and $\ell_{2}$, which are also $a$ units apart. The square $A B C D$ is placed on the plane so that sides $A B$ and $A D$ intersect $\ell_{1}$ at $E$ and $F$ respectively. Also, sides $C B$ and $C D$ intersect $\ell_{2}$ at $G$ and $H$ respectively. Let the perimeters of $\triangle A E F$ and $\triangle C G H$ be $m_{1}$ and $m_{2}$ respectively. Prove that no matter how the square was placed, $m_{1}+m_{2}$ remains constant.
|
Without loss of generality, assume the square has side $a=1$. Let $\theta$ be the acute angle between $\ell_{1}$ (or $\ell_{2}$ ) and the sides $A B$ and $C D$ of the square. Then, letting $E F=x$ and $G H=y$, we have
$$
E A=x \cos \theta, \quad A F=x \sin \theta, \quad C H=y \cos \theta, \quad C G=y \sin \theta
$$
Thus
$$
m_{1}+m_{2}=(x+y)(\sin \theta+\cos \theta+1) . \quad[2 \text { marks }]
$$
Draw lines parallel to $\ell_{1}, \ell_{2}$ through $A$ and $C$ respectively. The distance between these lines is $\sin \theta+\cos \theta$ [1 mark], as can be seen by drawing a mutual perpendicular to these lines through $B$, say. Also, the altitudes from $A$ to $E F$ and from $C$ to $G H$ have lengths $x \sin \theta \cos \theta$ and $y \sin \theta \cos \theta$ respectively [ 1 mark]. Therefore the distance between $\ell_{1}$ and $\ell_{2}$ must be
$$
(\sin \theta+\cos \theta)-x \sin \theta \cos \theta-y \sin \theta \cos \theta
$$
But we are given that this distance is $a=1$, so
$$
(x+y) \sin \theta \cos \theta+1=\sin \theta+\cos \theta
$$
or
$$
x+y=\frac{\sin \theta+\cos \theta-1}{\sin \theta \cos \theta} \cdot \quad[1 \text { mark }]
$$
Therefore, by (1),
$$
\begin{aligned}
m_{1}+m_{2} & =\frac{(\sin \theta+\cos \theta-1)(\sin \theta+\cos \theta+1)}{\sin \theta \cos \theta} \\
& =\frac{\left(\sin ^{2} \theta+\cos ^{2} \theta+2 \sin \theta \cos \theta\right)-1}{\sin \theta \cos \theta} \\
& =\frac{1+2 \sin \theta \cos \theta-1}{\sin \theta \cos \theta}=2 . \quad[2 \text { marks }]
\end{aligned}
$$
|
{
"resource_path": "APMO/segmented/en-apmo2003_sol.jsonl",
"problem_match": "\n2. ",
"solution_match": "\nSolution 3."
}
|
7f6794c9-bcf3-597c-a014-c2208022ac08
| 607,120
|
Let $k \geq 14$ be an integer, and let $p_{k}$ be the largest prime number which is strictly less than $k$. You may assume that $p_{k} \geq 3 k / 4$. Let $n$ be a composite integer. Prove:
(a) if $n=2 p_{k}$, then $n$ does not divide $(n-k)$ !;
(b) if $n>2 p_{k}$, then $n$ divides $(n-k)$ !.
|
(a) Note that $n-k=2 p_{k}-k<2 p_{k}-p_{k}=p_{k}$, so $p_{k} \nmid(n-k)$ !, so $2 p_{k} \nless(n-k)$ !. [1 mark]
(b) Note that $n>2 p_{k} \geq 3 k / 2$ implies $k<2 n / 3$, so $n-k>n / 3$. So if we can find integers $a, b \geq 3$ such that $n=a b$ and $a \neq b$, then both $a$ and $b$ will appear separately in the product $(n-k)!=1 \times 2 \times \cdots \times(n-k)$, which means $n \mid(n-k)!$. Observe that $k \geq 14$ implies $p_{k} \geq 13$, so that $n>2 p_{k} \geq 26$.
If $n=2^{\alpha}$ for some integer $\alpha \geq 5$, then take $a=2^{2}, b=2^{\alpha-2}$. [ 1 mark] Otherwise, since $n \geq 26>16$, we can take $a$ to be an odd prime factor of $n$ and $b=n / a$ [1 mark], unless $b<3$ or $b=a$.
Case (i): $b<3$. Since $n$ is composite, this means $b=2$, so that $2 a=n>2 p_{k}$. As $a$ is a prime number and $p_{k}$ is the largest prime number which is strictly less than $k$, it follows that $a \geq k$. From $n-k=2 a-k \geq$ $2 a-a=a>2$ we see that $n=2 a$ divides into $(n-k)$. [ 2 marks]
Case (ii): $b=a$. Then $n=a^{2}$ and $a>6$ since $n \geq 26$. Thus $n-k>n / 3=a^{2} / 3>2 a$, so that both $a$ and $2 a$ appear among $\{1,2, \ldots, n-k\}$. Hence $n=a^{2}$ divides into $(n-k)!$. [2 marks]
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $k \geq 14$ be an integer, and let $p_{k}$ be the largest prime number which is strictly less than $k$. You may assume that $p_{k} \geq 3 k / 4$. Let $n$ be a composite integer. Prove:
(a) if $n=2 p_{k}$, then $n$ does not divide $(n-k)$ !;
(b) if $n>2 p_{k}$, then $n$ divides $(n-k)$ !.
|
(a) Note that $n-k=2 p_{k}-k<2 p_{k}-p_{k}=p_{k}$, so $p_{k} \nmid(n-k)$ !, so $2 p_{k} \nless(n-k)$ !. [1 mark]
(b) Note that $n>2 p_{k} \geq 3 k / 2$ implies $k<2 n / 3$, so $n-k>n / 3$. So if we can find integers $a, b \geq 3$ such that $n=a b$ and $a \neq b$, then both $a$ and $b$ will appear separately in the product $(n-k)!=1 \times 2 \times \cdots \times(n-k)$, which means $n \mid(n-k)!$. Observe that $k \geq 14$ implies $p_{k} \geq 13$, so that $n>2 p_{k} \geq 26$.
If $n=2^{\alpha}$ for some integer $\alpha \geq 5$, then take $a=2^{2}, b=2^{\alpha-2}$. [ 1 mark] Otherwise, since $n \geq 26>16$, we can take $a$ to be an odd prime factor of $n$ and $b=n / a$ [1 mark], unless $b<3$ or $b=a$.
Case (i): $b<3$. Since $n$ is composite, this means $b=2$, so that $2 a=n>2 p_{k}$. As $a$ is a prime number and $p_{k}$ is the largest prime number which is strictly less than $k$, it follows that $a \geq k$. From $n-k=2 a-k \geq$ $2 a-a=a>2$ we see that $n=2 a$ divides into $(n-k)$. [ 2 marks]
Case (ii): $b=a$. Then $n=a^{2}$ and $a>6$ since $n \geq 26$. Thus $n-k>n / 3=a^{2} / 3>2 a$, so that both $a$ and $2 a$ appear among $\{1,2, \ldots, n-k\}$. Hence $n=a^{2}$ divides into $(n-k)!$. [2 marks]
|
{
"resource_path": "APMO/segmented/en-apmo2003_sol.jsonl",
"problem_match": "\n3. ",
"solution_match": "\nSolution."
}
|
9a6b26c4-8d6d-578f-afec-47d1fe749184
| 607,121
|
Let $a, b, c$ be the sides of a triangle, with $a+b+c=1$, and let $n \geq 2$ be an integer. Show that
$$
\sqrt[n]{a^{n}+b^{n}}+\sqrt[n]{b^{n}+c^{n}}+\sqrt[n]{c^{n}+a^{n}}<1+\frac{\sqrt[n]{2}}{2}
$$
|
Without loss of generality, assume $a \leq b \leq c$. As $a+b>c$, we have
$$
\frac{\sqrt[n]{2}}{2}=\frac{\sqrt[n]{2}}{2}(a+b+c)>\frac{\sqrt[n]{2}}{2}(c+c)=\sqrt[n]{2 c^{n}} \geq \sqrt[n]{b^{n}+c^{n}} \quad \quad[2 \text { marks }]
$$
As $a \leq c$ and $n \geq 2$, we have
$$
\begin{aligned}
\left(c^{n}+a^{n}\right)-\left(c+\frac{a}{2}\right)^{n} & =a^{n}-\sum_{k=1}^{n}\binom{n}{k} c^{n-k}\left(\frac{a}{2}\right)^{k} \\
& \leq\left[1-\sum_{k=1}^{n}\binom{n}{k}\left(\frac{1}{2}\right)^{k}\right] a^{n} \quad\left(\text { since } c^{n-k} \geq a^{n-k}\right) \\
& =\left[\left(1-\frac{n}{2}\right)-\sum_{k=2}^{n}\binom{n}{k}\left(\frac{1}{2}\right)^{k}\right] a^{n}<0
\end{aligned}
$$
Thus
$$
\sqrt[n]{c^{n}+a^{n}}<c+\frac{a}{2} . \quad[3 \text { marks }]
$$
Likewise
$$
\sqrt[n]{b^{n}+a^{n}}<b+\frac{a}{2} \quad \quad[1 \text { mark }]
$$
Adding (1), (2) and (3), we get
$$
\sqrt[n]{a^{n}+b^{n}}+\sqrt[n]{b^{n}+c^{n}}+\sqrt[n]{c^{n}+a^{n}}<\frac{\sqrt[n]{2}}{2}+c+\frac{a}{2}+b+\frac{a}{2}=1+\frac{\sqrt[n]{2}}{2} . \quad[1 \text { mark }]
$$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be the sides of a triangle, with $a+b+c=1$, and let $n \geq 2$ be an integer. Show that
$$
\sqrt[n]{a^{n}+b^{n}}+\sqrt[n]{b^{n}+c^{n}}+\sqrt[n]{c^{n}+a^{n}}<1+\frac{\sqrt[n]{2}}{2}
$$
|
Without loss of generality, assume $a \leq b \leq c$. As $a+b>c$, we have
$$
\frac{\sqrt[n]{2}}{2}=\frac{\sqrt[n]{2}}{2}(a+b+c)>\frac{\sqrt[n]{2}}{2}(c+c)=\sqrt[n]{2 c^{n}} \geq \sqrt[n]{b^{n}+c^{n}} \quad \quad[2 \text { marks }]
$$
As $a \leq c$ and $n \geq 2$, we have
$$
\begin{aligned}
\left(c^{n}+a^{n}\right)-\left(c+\frac{a}{2}\right)^{n} & =a^{n}-\sum_{k=1}^{n}\binom{n}{k} c^{n-k}\left(\frac{a}{2}\right)^{k} \\
& \leq\left[1-\sum_{k=1}^{n}\binom{n}{k}\left(\frac{1}{2}\right)^{k}\right] a^{n} \quad\left(\text { since } c^{n-k} \geq a^{n-k}\right) \\
& =\left[\left(1-\frac{n}{2}\right)-\sum_{k=2}^{n}\binom{n}{k}\left(\frac{1}{2}\right)^{k}\right] a^{n}<0
\end{aligned}
$$
Thus
$$
\sqrt[n]{c^{n}+a^{n}}<c+\frac{a}{2} . \quad[3 \text { marks }]
$$
Likewise
$$
\sqrt[n]{b^{n}+a^{n}}<b+\frac{a}{2} \quad \quad[1 \text { mark }]
$$
Adding (1), (2) and (3), we get
$$
\sqrt[n]{a^{n}+b^{n}}+\sqrt[n]{b^{n}+c^{n}}+\sqrt[n]{c^{n}+a^{n}}<\frac{\sqrt[n]{2}}{2}+c+\frac{a}{2}+b+\frac{a}{2}=1+\frac{\sqrt[n]{2}}{2} . \quad[1 \text { mark }]
$$
|
{
"resource_path": "APMO/segmented/en-apmo2003_sol.jsonl",
"problem_match": "\n4. ",
"solution_match": "# Solution."
}
|
b79cc3ed-c8e3-5cf0-ac83-ddeed2f10e82
| 607,122
|
Given two positive integers $m$ and $n$, find the smallest positive integer $k$ such that among any $k$ people, either there are $2 m$ of them who form $m$ pairs of mutually acquainted people or there are $2 n$ of them forming $n$ pairs of mutually unacquainted people.
|
Let the smallest positive integer $k$ satisfying the condition of the problem be denoted $r(m, n)$. We shall show that
$$
r(m, n)=2(m+n)-\min \{m, n\}-1
$$
Observe that, by symmetry, $r(m, n)=r(n, m)$. Therefore it suffices to consider the case where $m \geq n$, and to prove that
$$
r(m, n)=2 m+n-1 . \quad[1 \text { mark }]
$$
First we prove that
$$
r(m, n) \geq 2 m+n-1
$$
by an example. Call a group of $k$ people, every two of whom are mutually acquainted, a $k$-clique. Consider a set of $2 m+n-2$ people consisting of a $(2 m-1)$-clique together with an additional $n-1$ people none of whom know anyone else. (Call such people isolated.) Then there are not $2 m$ people forming $m$ mutually acquainted pairs, and there also are not $2 n$ people forming $n$ mutually unacquainted pairs. Thus $r(m, n) \geq$ $(2 m-1)+(n-1)+1=2 m+n-1$ by the definition of $r(m, n)$. [1 mark]
To establish (1), we need to prove that $r(m, n) \leq 2 m+n-1$. To do this, we now show that
$$
r(m, n) \leq r(m-1, n-1)+3 \quad \text { for all } m \geq n \geq 2
$$
Let $G$ be a group of $t=r(m-1, n-1)+3$ people. Notice that
$$
t \geq 2(m-1)+(n-1)-1+3=2 m+n-1 \geq 2 m \geq 2 n
$$
If $G$ is a $t$-clique, then $G$ contains $2 m$ people forming $m$ mutually acquainted pairs, and if $G$ has only isolated people, then $G$ contains $2 n$ people forming $n$ mutually unacquainted pairs. Otherwise, there are three people in $G$, say $a, b$ and $c$, such that $a, b$ are acquainted but $a, c$ are not. Now consider the group $A$ obtained byremoving $a, b$ and $c$ from $G$. A has $t-3=r(m-1, n-1)$ people, so by the definition of $r(m-1, n-1)$, A either contains $2(m-1)$ people forming $m-1$ mutually acquainted pairs, or else contains $2(n-1)$ people forming $n-1$ mutually unacquainted pairs. In the former case, we add the acquainted pair $a, b$ to $A$ to form $m$ mutually acquainted pairs in $G$. In the latter case, we add the unacquainted pair $a, c$ to $A$ to form $n$ mutually unacquainted pairs in $G$. This proves (2). [3 marks]
Trivially, $r(s, 1)=2 s$ for all $s[\mathbf{1}$ mark], so $r(m, n) \leq 2 m+n-1$ holds whenever $n=1$. Proceeding by induction on $n$, by (2) we obtain
$$
r(m, n) \leq r(m-1, n-1)+3 \leq 2(m-1)+(n-1)-1+3=2 m+n-1
$$
which completes the proof. [1 mark]
Note. Give an additional 1 mark to any student who gets at most 5 marks by the above marking scheme, but in addition gives a valid argument that $r(2,2)=5$.
|
r(m, n)=2 m+n-1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Given two positive integers $m$ and $n$, find the smallest positive integer $k$ such that among any $k$ people, either there are $2 m$ of them who form $m$ pairs of mutually acquainted people or there are $2 n$ of them forming $n$ pairs of mutually unacquainted people.
|
Let the smallest positive integer $k$ satisfying the condition of the problem be denoted $r(m, n)$. We shall show that
$$
r(m, n)=2(m+n)-\min \{m, n\}-1
$$
Observe that, by symmetry, $r(m, n)=r(n, m)$. Therefore it suffices to consider the case where $m \geq n$, and to prove that
$$
r(m, n)=2 m+n-1 . \quad[1 \text { mark }]
$$
First we prove that
$$
r(m, n) \geq 2 m+n-1
$$
by an example. Call a group of $k$ people, every two of whom are mutually acquainted, a $k$-clique. Consider a set of $2 m+n-2$ people consisting of a $(2 m-1)$-clique together with an additional $n-1$ people none of whom know anyone else. (Call such people isolated.) Then there are not $2 m$ people forming $m$ mutually acquainted pairs, and there also are not $2 n$ people forming $n$ mutually unacquainted pairs. Thus $r(m, n) \geq$ $(2 m-1)+(n-1)+1=2 m+n-1$ by the definition of $r(m, n)$. [1 mark]
To establish (1), we need to prove that $r(m, n) \leq 2 m+n-1$. To do this, we now show that
$$
r(m, n) \leq r(m-1, n-1)+3 \quad \text { for all } m \geq n \geq 2
$$
Let $G$ be a group of $t=r(m-1, n-1)+3$ people. Notice that
$$
t \geq 2(m-1)+(n-1)-1+3=2 m+n-1 \geq 2 m \geq 2 n
$$
If $G$ is a $t$-clique, then $G$ contains $2 m$ people forming $m$ mutually acquainted pairs, and if $G$ has only isolated people, then $G$ contains $2 n$ people forming $n$ mutually unacquainted pairs. Otherwise, there are three people in $G$, say $a, b$ and $c$, such that $a, b$ are acquainted but $a, c$ are not. Now consider the group $A$ obtained byremoving $a, b$ and $c$ from $G$. A has $t-3=r(m-1, n-1)$ people, so by the definition of $r(m-1, n-1)$, A either contains $2(m-1)$ people forming $m-1$ mutually acquainted pairs, or else contains $2(n-1)$ people forming $n-1$ mutually unacquainted pairs. In the former case, we add the acquainted pair $a, b$ to $A$ to form $m$ mutually acquainted pairs in $G$. In the latter case, we add the unacquainted pair $a, c$ to $A$ to form $n$ mutually unacquainted pairs in $G$. This proves (2). [3 marks]
Trivially, $r(s, 1)=2 s$ for all $s[\mathbf{1}$ mark], so $r(m, n) \leq 2 m+n-1$ holds whenever $n=1$. Proceeding by induction on $n$, by (2) we obtain
$$
r(m, n) \leq r(m-1, n-1)+3 \leq 2(m-1)+(n-1)-1+3=2 m+n-1
$$
which completes the proof. [1 mark]
Note. Give an additional 1 mark to any student who gets at most 5 marks by the above marking scheme, but in addition gives a valid argument that $r(2,2)=5$.
|
{
"resource_path": "APMO/segmented/en-apmo2003_sol.jsonl",
"problem_match": "\n5. ",
"solution_match": "# Solution."
}
|
7f39ab2a-ac8a-548f-ade3-e2e407eeb898
| 607,123
|
Determine all finite nonempty sets $S$ of positive integers satisfying
$$
\frac{i+j}{(i, j)} \text { is an element of } S \text { for all } i, j \text { in } S \text {, }
$$
where $(i, j)$ is the greatest common divisor of $i$ and $j$.
Answer: $S=\{2\}$.
|
Let $k \in S$. Then $\frac{k+k}{(k, k)}=2$ is in $S$ as well.
Suppose for the sake of contradiction that there is an odd number in $S$, and let $k$ be the largest such odd number. Since $(k, 2)=1, \frac{k+2}{(k, 2)}=k+2>k$ is in $S$ as well, a contradiction. Hence $S$ has no odd numbers.
Now suppose that $\ell>2$ is the second smallest number in $S$. Then $\ell$ is even and $\frac{\ell+2}{(\ell, 2)}=\frac{\ell}{2}+1$ is in $S$. Since $\ell>2 \Longrightarrow \frac{\ell}{2}+1>2, \frac{\ell}{2}+1 \geq \ell \Longleftrightarrow \ell \leq 2$, a contradiction again.
Therefore $S$ can only contain 2 , and $S=\{2\}$ is the only solution.
|
S=\{2\}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Determine all finite nonempty sets $S$ of positive integers satisfying
$$
\frac{i+j}{(i, j)} \text { is an element of } S \text { for all } i, j \text { in } S \text {, }
$$
where $(i, j)$ is the greatest common divisor of $i$ and $j$.
Answer: $S=\{2\}$.
|
Let $k \in S$. Then $\frac{k+k}{(k, k)}=2$ is in $S$ as well.
Suppose for the sake of contradiction that there is an odd number in $S$, and let $k$ be the largest such odd number. Since $(k, 2)=1, \frac{k+2}{(k, 2)}=k+2>k$ is in $S$ as well, a contradiction. Hence $S$ has no odd numbers.
Now suppose that $\ell>2$ is the second smallest number in $S$. Then $\ell$ is even and $\frac{\ell+2}{(\ell, 2)}=\frac{\ell}{2}+1$ is in $S$. Since $\ell>2 \Longrightarrow \frac{\ell}{2}+1>2, \frac{\ell}{2}+1 \geq \ell \Longleftrightarrow \ell \leq 2$, a contradiction again.
Therefore $S$ can only contain 2 , and $S=\{2\}$ is the only solution.
|
{
"resource_path": "APMO/segmented/en-apmo2004_sol.jsonl",
"problem_match": "# Problem 1",
"solution_match": "# Solution\n\n"
}
|
f6a93166-e0d9-547f-b691-ea14abdd8077
| 604,827
|
Let $O$ be the circumcentre and $H$ the orthocentre of an acute triangle $A B C$. Prove that the area of one of the triangles $\mathrm{AOH}, \mathrm{BOH}$ and COH is equal to the sum of the areas of the other two.
|
Suppose, without loss of generality, that $B$ and $C$ lies in the same side of line $O H$. Such line is the Euler line of $A B C$, so the centroid $G$ lies in this line.
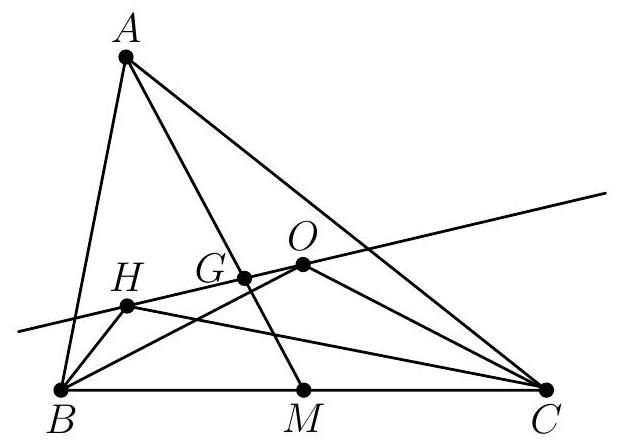
Let $M$ be the midpoint of $B C$. Then the distance between $M$ and the line $O H$ is the average of the distances from $B$ and C to OH , and the sum of the areas of triangles BOH and COH is
$$
[B O H]+[C O H]=\frac{O H \cdot d(B, O H)}{2}+\frac{O H \cdot d(C, O H)}{2}=\frac{O H \cdot 2 d(M, O H)}{2} .
$$
Since $A G=2 G M, d(A, O H)=2 d(M, O H)$. Hence
$$
[B O H]+[C O H]=\frac{O H \cdot d(A, O H)}{2}=[A O H]
$$
and the result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $O$ be the circumcentre and $H$ the orthocentre of an acute triangle $A B C$. Prove that the area of one of the triangles $\mathrm{AOH}, \mathrm{BOH}$ and COH is equal to the sum of the areas of the other two.
|
Suppose, without loss of generality, that $B$ and $C$ lies in the same side of line $O H$. Such line is the Euler line of $A B C$, so the centroid $G$ lies in this line.

Let $M$ be the midpoint of $B C$. Then the distance between $M$ and the line $O H$ is the average of the distances from $B$ and C to OH , and the sum of the areas of triangles BOH and COH is
$$
[B O H]+[C O H]=\frac{O H \cdot d(B, O H)}{2}+\frac{O H \cdot d(C, O H)}{2}=\frac{O H \cdot 2 d(M, O H)}{2} .
$$
Since $A G=2 G M, d(A, O H)=2 d(M, O H)$. Hence
$$
[B O H]+[C O H]=\frac{O H \cdot d(A, O H)}{2}=[A O H]
$$
and the result follows.
|
{
"resource_path": "APMO/segmented/en-apmo2004_sol.jsonl",
"problem_match": "# Problem 2",
"solution_match": "# Solution 1"
}
|
3d8f831e-00b1-5b0f-b0b0-17aa6bd4254d
| 604,841
|
Let $O$ be the circumcentre and $H$ the orthocentre of an acute triangle $A B C$. Prove that the area of one of the triangles $\mathrm{AOH}, \mathrm{BOH}$ and COH is equal to the sum of the areas of the other two.
|
One can use barycentric coordinates: it is well known that
$$
\begin{gathered}
A=(1: 0: 0), \quad B=(0: 1: 0), \quad C=(0: 0: 1), \\
O=(\sin 2 A: \sin 2 B: \sin 2 C) \quad \text { and } \quad H=(\tan A: \tan B: \tan C) .
\end{gathered}
$$
Then the (signed) area of $A O H$ is proportional to
$$
\left|\begin{array}{ccc}
1 & 0 & 0 \\
\sin 2 A & \sin 2 B & \sin 2 C \\
\tan A & \tan B & \tan C
\end{array}\right|
$$
Adding all three expressions we find that the sum of the signed sums of the areas is a constant times
$$
\left|\begin{array}{ccc}
1 & 0 & 0 \\
\sin 2 A & \sin 2 B & \sin 2 C \\
\tan A & \tan B & \tan C
\end{array}\right|+\left|\begin{array}{ccc}
0 & 1 & 0 \\
\sin 2 A & \sin 2 B & \sin 2 C \\
\tan A & \tan B & \tan C
\end{array}\right|+\left|\begin{array}{ccc}
0 & 0 & 1 \\
\sin 2 A & \sin 2 B & \sin 2 C \\
\tan A & \tan B & \tan C
\end{array}\right|
$$
By multilinearity of the determinant, this sum equals
$$
\left|\begin{array}{ccc}
1 & 1 & 1 \\
\sin 2 A & \sin 2 B & \sin 2 C \\
\tan A & \tan B & \tan C
\end{array}\right|
$$
which contains, in its rows, the coordinates of the centroid, the circumcenter, and the orthocenter. Since these three points lie in the Euler line of $A B C$, the signed sum of the areas is 0 , which means that one of the areas of $A O H, B O H, C O H$ is the sum of the other two areas.
Comment: Both solutions can be adapted to prove a stronger result: if the centroid $G$ of triangle $A B C$ belongs to line $X Y$ then one of the areas of triangles $A X Y, B X Y$, and $C X Y$ is equal to the sum of the other two.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $O$ be the circumcentre and $H$ the orthocentre of an acute triangle $A B C$. Prove that the area of one of the triangles $\mathrm{AOH}, \mathrm{BOH}$ and COH is equal to the sum of the areas of the other two.
|
One can use barycentric coordinates: it is well known that
$$
\begin{gathered}
A=(1: 0: 0), \quad B=(0: 1: 0), \quad C=(0: 0: 1), \\
O=(\sin 2 A: \sin 2 B: \sin 2 C) \quad \text { and } \quad H=(\tan A: \tan B: \tan C) .
\end{gathered}
$$
Then the (signed) area of $A O H$ is proportional to
$$
\left|\begin{array}{ccc}
1 & 0 & 0 \\
\sin 2 A & \sin 2 B & \sin 2 C \\
\tan A & \tan B & \tan C
\end{array}\right|
$$
Adding all three expressions we find that the sum of the signed sums of the areas is a constant times
$$
\left|\begin{array}{ccc}
1 & 0 & 0 \\
\sin 2 A & \sin 2 B & \sin 2 C \\
\tan A & \tan B & \tan C
\end{array}\right|+\left|\begin{array}{ccc}
0 & 1 & 0 \\
\sin 2 A & \sin 2 B & \sin 2 C \\
\tan A & \tan B & \tan C
\end{array}\right|+\left|\begin{array}{ccc}
0 & 0 & 1 \\
\sin 2 A & \sin 2 B & \sin 2 C \\
\tan A & \tan B & \tan C
\end{array}\right|
$$
By multilinearity of the determinant, this sum equals
$$
\left|\begin{array}{ccc}
1 & 1 & 1 \\
\sin 2 A & \sin 2 B & \sin 2 C \\
\tan A & \tan B & \tan C
\end{array}\right|
$$
which contains, in its rows, the coordinates of the centroid, the circumcenter, and the orthocenter. Since these three points lie in the Euler line of $A B C$, the signed sum of the areas is 0 , which means that one of the areas of $A O H, B O H, C O H$ is the sum of the other two areas.
Comment: Both solutions can be adapted to prove a stronger result: if the centroid $G$ of triangle $A B C$ belongs to line $X Y$ then one of the areas of triangles $A X Y, B X Y$, and $C X Y$ is equal to the sum of the other two.
|
{
"resource_path": "APMO/segmented/en-apmo2004_sol.jsonl",
"problem_match": "# Problem 2",
"solution_match": "# Solution 2"
}
|
3d8f831e-00b1-5b0f-b0b0-17aa6bd4254d
| 604,841
|
Let a set $S$ of 2004 points in the plane be given, no three of which are collinear. Let $\mathcal{L}$ denote the set of all lines (extended indefinitely in both directions) determined by pairs of points from the set. Show that it is possible to colour the points of $S$ with at most two colours, such that for any points $p, q$ of $S$, the number of lines in $\mathcal{L}$ which separate $p$ from $q$ is odd if and only if $p$ and $q$ have the same colour.
Note: A line $\ell$ separates two points $p$ and $q$ if $p$ and $q$ lie on opposite sides of $\ell$ with neither point on $\ell$.
|
Choose any point $p$ from $S$ and color it, say, blue. Let $n(q, r)$ be the number of lines from $\mathcal{L}$ that separates $q$ and $r$. Then color any other point $q$ blue if $n(p, q)$ is odd and red if $n(p, q)$ is even.
Now it remains to show that $q$ and $r$ have the same color if and only if $n(q, r)$ is odd for all $q \neq p$ and $r \neq p$, which is equivalent to proving that $n(p, q)+n(p, r)+n(q, r)$ is always odd. For this purpose, consider the seven numbered regions defined by lines $p q$, $p r$, and $q r$ :
Any line that do not pass through any of points $p, q, r$ meets the sides $p q, q r, p r$ of triangle $p q r$ in an even number of points (two sides or no sides), so these lines do not affect the parity of $n(p, q)+n(p, r)+n(q, r)$. Hence the only lines that need to be considered are the ones that pass through one of vertices $p, q, r$ and cuts the opposite side in the triangle $p q r$.
Let $n_{i}$ be the number of points in region $i, p, q$, and $r$ excluded, as depicted in the diagram. Then the lines through $p$ that separate $q$ and $r$ are the lines passing through $p$ and points from regions 1,4 , and 7 . The same applies for $p, q$ and regions 2,5 , and 7 ; and $p, r$ and regions 3,6 , and 7. Therefore
$$
\begin{aligned}
n(p, q)+n(q, r)+n(p, r) & \equiv\left(n_{2}+n_{5}+n_{7}\right)+\left(n_{1}+n_{4}+n_{7}\right)+\left(n_{3}+n_{6}+n_{7}\right) \\
& \equiv n_{1}+n_{2}+n_{3}+n_{4}+n_{5}+n_{6}+n_{7}=2004-3 \equiv 1 \quad(\bmod 2)
\end{aligned}
$$
and the result follows.
Comment: The problem statement is also true if 2004 is replaced by any even number and is not true if 2004 is replaced by any odd number greater than 1.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let a set $S$ of 2004 points in the plane be given, no three of which are collinear. Let $\mathcal{L}$ denote the set of all lines (extended indefinitely in both directions) determined by pairs of points from the set. Show that it is possible to colour the points of $S$ with at most two colours, such that for any points $p, q$ of $S$, the number of lines in $\mathcal{L}$ which separate $p$ from $q$ is odd if and only if $p$ and $q$ have the same colour.
Note: A line $\ell$ separates two points $p$ and $q$ if $p$ and $q$ lie on opposite sides of $\ell$ with neither point on $\ell$.
|
Choose any point $p$ from $S$ and color it, say, blue. Let $n(q, r)$ be the number of lines from $\mathcal{L}$ that separates $q$ and $r$. Then color any other point $q$ blue if $n(p, q)$ is odd and red if $n(p, q)$ is even.
Now it remains to show that $q$ and $r$ have the same color if and only if $n(q, r)$ is odd for all $q \neq p$ and $r \neq p$, which is equivalent to proving that $n(p, q)+n(p, r)+n(q, r)$ is always odd. For this purpose, consider the seven numbered regions defined by lines $p q$, $p r$, and $q r$ :

Any line that do not pass through any of points $p, q, r$ meets the sides $p q, q r, p r$ of triangle $p q r$ in an even number of points (two sides or no sides), so these lines do not affect the parity of $n(p, q)+n(p, r)+n(q, r)$. Hence the only lines that need to be considered are the ones that pass through one of vertices $p, q, r$ and cuts the opposite side in the triangle $p q r$.
Let $n_{i}$ be the number of points in region $i, p, q$, and $r$ excluded, as depicted in the diagram. Then the lines through $p$ that separate $q$ and $r$ are the lines passing through $p$ and points from regions 1,4 , and 7 . The same applies for $p, q$ and regions 2,5 , and 7 ; and $p, r$ and regions 3,6 , and 7. Therefore
$$
\begin{aligned}
n(p, q)+n(q, r)+n(p, r) & \equiv\left(n_{2}+n_{5}+n_{7}\right)+\left(n_{1}+n_{4}+n_{7}\right)+\left(n_{3}+n_{6}+n_{7}\right) \\
& \equiv n_{1}+n_{2}+n_{3}+n_{4}+n_{5}+n_{6}+n_{7}=2004-3 \equiv 1 \quad(\bmod 2)
\end{aligned}
$$
and the result follows.
Comment: The problem statement is also true if 2004 is replaced by any even number and is not true if 2004 is replaced by any odd number greater than 1.
|
{
"resource_path": "APMO/segmented/en-apmo2004_sol.jsonl",
"problem_match": "# Problem 3",
"solution_match": "# Solution\n\n"
}
|
0a9dc559-c5b2-5327-9624-e2ad03392ef8
| 604,863
|
For a real number $x$, let $\lfloor x\rfloor$ stand for the largest integer that is less than or equal to $x$. Prove that
$$
\left\lfloor\frac{(n-1)!}{n(n+1)}\right\rfloor
$$
is even for every positive integer $n$.
|
Consider four cases:
- $n \leq 5$. Then $\left\lfloor\frac{(n-1)!}{n(n+1)}\right\rfloor=0$ is an even number.
- $n$ and $n+1$ are both composite (in particular, $n \geq 8$ ). Then $n=a b$ and $n+1=c d$ for $a, b, c, d \geq 2$. Moreover, since $n$ and $n+1$ are coprime, $a, b, c, d$ are all distinct and smaller than $n$, and one can choose $a, b, c, d$ such that exactly one of these four numbers is even. Hence $\frac{(n-1)!}{n(n+1)}$ is an integer. As $n \geq 8>6,(n-1)!$ has at least three even factors, so $\frac{(n-1)!}{n(n+1)}$ is an even integer.
- $n \geq 7$ is an odd prime. By Wilson's theorem, $(n-1)!\equiv-1(\bmod n)$, that is, $\frac{(n-1)!+1}{n}$ is an integer, as $\frac{(n-1)!+n+1}{n}=\frac{(n-1)!+1}{n}+1$ is. As before, $\frac{(n-1)!}{n+1}$ is an even integer; therefore $\frac{(n-1)!+n+1}{n+1}=\frac{(n-1)!}{n+1}+1$ is an odd integer.
Also, $n$ and $n+1$ are coprime and $n$ divides the odd integer $\frac{(n-1)!+n+1}{n+1}$, so $\frac{(n-1)!+n+1}{n(n+1)}$ is also an odd integer. Then
$$
\left\lfloor\frac{(n-1)!}{n(n+1)}\right\rfloor=\frac{(n-1)!+n+1}{n(n+1)}-1
$$
is even.
- $n+1 \geq 7$ is an odd prime. Again, since $n$ is composite, $\frac{(n-1)!}{n}$ is an even integer, and $\frac{(n-1)!+n}{n}$ is an odd integer. By Wilson's theorem, $n!\equiv-1(\bmod n+1) \Longleftrightarrow(n-1)!\equiv 1$ $(\bmod n+1)$. This means that $n+1$ divides $(n-1)!+n$, and since $n$ and $n+1$ are coprime, $n+1$ also divides $\frac{(n-1)!+n}{n}$. Then $\frac{(n-1)!+n}{n(n+1)}$ is also an odd integer and
$$
\left\lfloor\frac{(n-1)!}{n(n+1)}\right\rfloor=\frac{(n-1)!+n}{n(n+1)}-1
$$
is even.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For a real number $x$, let $\lfloor x\rfloor$ stand for the largest integer that is less than or equal to $x$. Prove that
$$
\left\lfloor\frac{(n-1)!}{n(n+1)}\right\rfloor
$$
is even for every positive integer $n$.
|
Consider four cases:
- $n \leq 5$. Then $\left\lfloor\frac{(n-1)!}{n(n+1)}\right\rfloor=0$ is an even number.
- $n$ and $n+1$ are both composite (in particular, $n \geq 8$ ). Then $n=a b$ and $n+1=c d$ for $a, b, c, d \geq 2$. Moreover, since $n$ and $n+1$ are coprime, $a, b, c, d$ are all distinct and smaller than $n$, and one can choose $a, b, c, d$ such that exactly one of these four numbers is even. Hence $\frac{(n-1)!}{n(n+1)}$ is an integer. As $n \geq 8>6,(n-1)!$ has at least three even factors, so $\frac{(n-1)!}{n(n+1)}$ is an even integer.
- $n \geq 7$ is an odd prime. By Wilson's theorem, $(n-1)!\equiv-1(\bmod n)$, that is, $\frac{(n-1)!+1}{n}$ is an integer, as $\frac{(n-1)!+n+1}{n}=\frac{(n-1)!+1}{n}+1$ is. As before, $\frac{(n-1)!}{n+1}$ is an even integer; therefore $\frac{(n-1)!+n+1}{n+1}=\frac{(n-1)!}{n+1}+1$ is an odd integer.
Also, $n$ and $n+1$ are coprime and $n$ divides the odd integer $\frac{(n-1)!+n+1}{n+1}$, so $\frac{(n-1)!+n+1}{n(n+1)}$ is also an odd integer. Then
$$
\left\lfloor\frac{(n-1)!}{n(n+1)}\right\rfloor=\frac{(n-1)!+n+1}{n(n+1)}-1
$$
is even.
- $n+1 \geq 7$ is an odd prime. Again, since $n$ is composite, $\frac{(n-1)!}{n}$ is an even integer, and $\frac{(n-1)!+n}{n}$ is an odd integer. By Wilson's theorem, $n!\equiv-1(\bmod n+1) \Longleftrightarrow(n-1)!\equiv 1$ $(\bmod n+1)$. This means that $n+1$ divides $(n-1)!+n$, and since $n$ and $n+1$ are coprime, $n+1$ also divides $\frac{(n-1)!+n}{n}$. Then $\frac{(n-1)!+n}{n(n+1)}$ is also an odd integer and
$$
\left\lfloor\frac{(n-1)!}{n(n+1)}\right\rfloor=\frac{(n-1)!+n}{n(n+1)}-1
$$
is even.
|
{
"resource_path": "APMO/segmented/en-apmo2004_sol.jsonl",
"problem_match": "# Problem 4",
"solution_match": "# Solution\n\n"
}
|
110f7ed3-2dd7-5e0e-a16f-cc0238f9e851
| 604,876
|
Prove that
$$
\left(a^{2}+2\right)\left(b^{2}+2\right)\left(c^{2}+2\right) \geq 9(a b+b c+c a)
$$
for all real numbers $a, b, c>0$.
|
Let $p=a+b+c, q=a b+b c+c a$, and $r=a b c$. The inequality simplifies to
$$
a^{2} b^{2} c^{2}+2\left(a^{2} b^{2}+b^{2} c^{2}+c^{2} a^{2}\right)+4\left(a^{2}+b^{2}+c^{2}\right)+8-9(a b+b c+c a) \geq 0
$$
Since $a^{2} b^{2}+b^{2} c^{2}+c^{2} a^{2}=q^{2}-2 p r$ and $a^{2}+b^{2}+c^{2}=p^{2}-2 q$,
$$
r^{2}+2 q^{2}-4 p r+4 p^{2}-8 q+8-9 q \geq 0
$$
which simplifies to
$$
r^{2}+2 q^{2}+4 p^{2}-17 q-4 p r+8 \geq 0
$$
Bearing in mind that equality occurs for $a=b=c=1$, which means that, for instance, $p=3 r$, one can rewrite $(I)$ as
$$
\left(r-\frac{p}{3}\right)^{2}-\frac{10}{3} p r+\frac{35}{9} p^{2}+2 q^{2}-17 q+8 \geq 0
$$
Since $(a b-b c)^{2}+(b c-c a)^{2}+(c a-a b)^{2} \geq 0$ is equivalent to $q^{2} \geq 3 p r$, rewrite $(I I)$ as
$$
\left(r-\frac{p}{3}\right)^{2}+\frac{10}{9}\left(q^{2}-3 p r\right)+\frac{35}{9} p^{2}+\frac{8}{9} q^{2}-17 q+8 \geq 0
$$
Finally, $a=b=c=1$ implies $q=3$; then rewrite (III) as
$$
\left(r-\frac{p}{3}\right)^{2}+\frac{10}{9}\left(q^{2}-3 p r\right)+\frac{35}{9}\left(p^{2}-3 q\right)+\frac{8}{9}(q-3)^{2} \geq 0
$$
This final inequality is true because $q^{2} \geq 3 p r$ and $p^{2}-3 q=\frac{1}{2}\left[(a-b)^{2}+(b-c)^{2}+(c-a)^{2}\right] \geq 0$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prove that
$$
\left(a^{2}+2\right)\left(b^{2}+2\right)\left(c^{2}+2\right) \geq 9(a b+b c+c a)
$$
for all real numbers $a, b, c>0$.
|
Let $p=a+b+c, q=a b+b c+c a$, and $r=a b c$. The inequality simplifies to
$$
a^{2} b^{2} c^{2}+2\left(a^{2} b^{2}+b^{2} c^{2}+c^{2} a^{2}\right)+4\left(a^{2}+b^{2}+c^{2}\right)+8-9(a b+b c+c a) \geq 0
$$
Since $a^{2} b^{2}+b^{2} c^{2}+c^{2} a^{2}=q^{2}-2 p r$ and $a^{2}+b^{2}+c^{2}=p^{2}-2 q$,
$$
r^{2}+2 q^{2}-4 p r+4 p^{2}-8 q+8-9 q \geq 0
$$
which simplifies to
$$
r^{2}+2 q^{2}+4 p^{2}-17 q-4 p r+8 \geq 0
$$
Bearing in mind that equality occurs for $a=b=c=1$, which means that, for instance, $p=3 r$, one can rewrite $(I)$ as
$$
\left(r-\frac{p}{3}\right)^{2}-\frac{10}{3} p r+\frac{35}{9} p^{2}+2 q^{2}-17 q+8 \geq 0
$$
Since $(a b-b c)^{2}+(b c-c a)^{2}+(c a-a b)^{2} \geq 0$ is equivalent to $q^{2} \geq 3 p r$, rewrite $(I I)$ as
$$
\left(r-\frac{p}{3}\right)^{2}+\frac{10}{9}\left(q^{2}-3 p r\right)+\frac{35}{9} p^{2}+\frac{8}{9} q^{2}-17 q+8 \geq 0
$$
Finally, $a=b=c=1$ implies $q=3$; then rewrite (III) as
$$
\left(r-\frac{p}{3}\right)^{2}+\frac{10}{9}\left(q^{2}-3 p r\right)+\frac{35}{9}\left(p^{2}-3 q\right)+\frac{8}{9}(q-3)^{2} \geq 0
$$
This final inequality is true because $q^{2} \geq 3 p r$ and $p^{2}-3 q=\frac{1}{2}\left[(a-b)^{2}+(b-c)^{2}+(c-a)^{2}\right] \geq 0$.
|
{
"resource_path": "APMO/segmented/en-apmo2004_sol.jsonl",
"problem_match": "# Problem 5",
"solution_match": "# Solution 1"
}
|
85c2e20c-c2c5-5955-a346-fe489616b284
| 604,886
|
Prove that
$$
\left(a^{2}+2\right)\left(b^{2}+2\right)\left(c^{2}+2\right) \geq 9(a b+b c+c a)
$$
for all real numbers $a, b, c>0$.
|
We prove the stronger inequality
$$
\left(a^{2}+2\right)\left(b^{2}+2\right)\left(c^{2}+2\right) \geq 3(a+b+c)^{2}
$$
which implies the proposed inequality because $(a+b+c)^{2} \geq 3(a b+b c+c a)$ is equivalent to $(a-b)^{2}+(b-c)^{2}+(c-a)^{2} \geq 0$, which is immediate.
The inequality $(*)$ is equivalent to
$$
\left(\left(b^{2}+2\right)\left(c^{2}+2\right)-3\right) a^{2}-6(b+c) a+2\left(b^{2}+2\right)\left(c^{2}+2\right)-3(b+c)^{2} \geq 0
$$
Seeing this inequality as a quadratic inequality in $a$ with positive leading coefficient $\left(b^{2}+2\right)\left(c^{2}+\right.$ 2) $-3=b^{2} c^{2}+2 b^{2}+2 c^{2}+1$, it suffices to prove that its discriminant is non-positive, which is equivalent to
$$
(3(b+c))^{2}-\left(\left(b^{2}+2\right)\left(c^{2}+2\right)-3\right)\left(2\left(b^{2}+2\right)\left(c^{2}+2\right)-3(b+c)^{2}\right) \leq 0
$$
This simplifies to
$$
-2\left(b^{2}+2\right)\left(c^{2}+2\right)+3(b+c)^{2}+6 \leq 0
$$
Now we look $(* *)$ as a quadratic inequality in $b$ with negative leading coefficient $-2 c^{2}-1$ :
$$
\left(-2 c^{2}-1\right) b^{2}+6 c b-c^{2}-2 \leq 0
$$
If suffices to show that the discriminant of $(* *)$ is non-positive, which is equivalent to
$$
9 c^{2}-\left(2 c^{2}+1\right)\left(c^{2}+2\right) \leq 0
$$
It simplifies to $-2\left(c^{2}-1\right)^{2} \leq 0$, which is true. The equality occurs for $c^{2}=1$, that is, $c=1$, for which $b=\frac{6 c}{2\left(2 c^{2}+1\right)}=1$, and $a=\frac{6(b+c)}{2\left(\left(b^{2}+2\right)\left(c^{2}+2\right)-3\right)}=1$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prove that
$$
\left(a^{2}+2\right)\left(b^{2}+2\right)\left(c^{2}+2\right) \geq 9(a b+b c+c a)
$$
for all real numbers $a, b, c>0$.
|
We prove the stronger inequality
$$
\left(a^{2}+2\right)\left(b^{2}+2\right)\left(c^{2}+2\right) \geq 3(a+b+c)^{2}
$$
which implies the proposed inequality because $(a+b+c)^{2} \geq 3(a b+b c+c a)$ is equivalent to $(a-b)^{2}+(b-c)^{2}+(c-a)^{2} \geq 0$, which is immediate.
The inequality $(*)$ is equivalent to
$$
\left(\left(b^{2}+2\right)\left(c^{2}+2\right)-3\right) a^{2}-6(b+c) a+2\left(b^{2}+2\right)\left(c^{2}+2\right)-3(b+c)^{2} \geq 0
$$
Seeing this inequality as a quadratic inequality in $a$ with positive leading coefficient $\left(b^{2}+2\right)\left(c^{2}+\right.$ 2) $-3=b^{2} c^{2}+2 b^{2}+2 c^{2}+1$, it suffices to prove that its discriminant is non-positive, which is equivalent to
$$
(3(b+c))^{2}-\left(\left(b^{2}+2\right)\left(c^{2}+2\right)-3\right)\left(2\left(b^{2}+2\right)\left(c^{2}+2\right)-3(b+c)^{2}\right) \leq 0
$$
This simplifies to
$$
-2\left(b^{2}+2\right)\left(c^{2}+2\right)+3(b+c)^{2}+6 \leq 0
$$
Now we look $(* *)$ as a quadratic inequality in $b$ with negative leading coefficient $-2 c^{2}-1$ :
$$
\left(-2 c^{2}-1\right) b^{2}+6 c b-c^{2}-2 \leq 0
$$
If suffices to show that the discriminant of $(* *)$ is non-positive, which is equivalent to
$$
9 c^{2}-\left(2 c^{2}+1\right)\left(c^{2}+2\right) \leq 0
$$
It simplifies to $-2\left(c^{2}-1\right)^{2} \leq 0$, which is true. The equality occurs for $c^{2}=1$, that is, $c=1$, for which $b=\frac{6 c}{2\left(2 c^{2}+1\right)}=1$, and $a=\frac{6(b+c)}{2\left(\left(b^{2}+2\right)\left(c^{2}+2\right)-3\right)}=1$.
|
{
"resource_path": "APMO/segmented/en-apmo2004_sol.jsonl",
"problem_match": "# Problem 5",
"solution_match": "# Solution 2"
}
|
85c2e20c-c2c5-5955-a346-fe489616b284
| 604,886
|
Prove that
$$
\left(a^{2}+2\right)\left(b^{2}+2\right)\left(c^{2}+2\right) \geq 9(a b+b c+c a)
$$
for all real numbers $a, b, c>0$.
|
Let $A, B, C$ angles in $(0, \pi / 2)$ such that $a=\sqrt{2} \tan A, b=\sqrt{2} \tan B$, and $c=\sqrt{2} \tan C$. Then the inequality is equivalent to
$$
4 \sec ^{2} A \sec ^{2} B \sec ^{2} C \geq 9(\tan A \tan B+\tan B \tan C+\tan C \tan A)
$$
Substituting $\sec x=\frac{1}{\cos x}$ for $x \in\{A, B, C\}$ and clearing denominators, the inequality is equivalent to
$$
\cos A \cos B \cos C(\sin A \sin B \cos C+\cos A \sin B \sin C+\sin A \cos B \sin C) \leq \frac{4}{9}
$$
Since
$$
\begin{aligned}
& \cos (A+B+C)=\cos A \cos (B+C)-\sin A \sin (B+C) \\
= & \cos A \cos B \cos C-\cos A \sin B \sin C-\sin A \cos B \sin C-\sin A \sin B \cos C,
\end{aligned}
$$
we rewrite our inequality as
$$
\cos A \cos B \cos C(\cos A \cos B \cos C-\cos (A+B+C)) \leq \frac{4}{9}
$$
The cosine function is concave down on $(0, \pi / 2)$. Therefore, if $\theta=\frac{A+B+C}{3}$, by the AM-GM inequality and Jensen's inequality,
$$
\cos A \cos B \cos C \leq\left(\frac{\cos A+\cos B+\cos C}{3}\right)^{3} \leq \cos ^{3} \frac{A+B+C}{3}=\cos ^{3} \theta
$$
Therefore, since $\cos A \cos B \cos C-\cos (A+B+C)=\sin A \sin B \cos C+\cos A \sin B \sin C+$ $\sin A \cos B \sin C>0$, and recalling that $\cos 3 \theta=4 \cos ^{3} \theta-3 \cos \theta$,
$\cos A \cos B \cos C(\cos A \cos B \cos C-\cos (A+B+C)) \leq \cos ^{3} \theta\left(\cos ^{3} \theta-\cos 3 \theta\right)=3 \cos ^{4} \theta\left(1-\cos ^{2} \theta\right)$. Finally, by AM-GM (notice that $1-\cos ^{2} \theta=\sin ^{2} \theta>0$ ),
$3 \cos ^{4} \theta\left(1-\cos ^{2} \theta\right)=\frac{3}{2} \cos ^{2} \theta \cdot \cos ^{2} \theta\left(2-2 \cos ^{2} \theta\right) \leq \frac{3}{2}\left(\frac{\cos ^{2} \theta+\cos ^{2} \theta+\left(2-2 \cos ^{2} \theta\right)}{3}\right)^{3}=\frac{4}{9}$,
and the result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prove that
$$
\left(a^{2}+2\right)\left(b^{2}+2\right)\left(c^{2}+2\right) \geq 9(a b+b c+c a)
$$
for all real numbers $a, b, c>0$.
|
Let $A, B, C$ angles in $(0, \pi / 2)$ such that $a=\sqrt{2} \tan A, b=\sqrt{2} \tan B$, and $c=\sqrt{2} \tan C$. Then the inequality is equivalent to
$$
4 \sec ^{2} A \sec ^{2} B \sec ^{2} C \geq 9(\tan A \tan B+\tan B \tan C+\tan C \tan A)
$$
Substituting $\sec x=\frac{1}{\cos x}$ for $x \in\{A, B, C\}$ and clearing denominators, the inequality is equivalent to
$$
\cos A \cos B \cos C(\sin A \sin B \cos C+\cos A \sin B \sin C+\sin A \cos B \sin C) \leq \frac{4}{9}
$$
Since
$$
\begin{aligned}
& \cos (A+B+C)=\cos A \cos (B+C)-\sin A \sin (B+C) \\
= & \cos A \cos B \cos C-\cos A \sin B \sin C-\sin A \cos B \sin C-\sin A \sin B \cos C,
\end{aligned}
$$
we rewrite our inequality as
$$
\cos A \cos B \cos C(\cos A \cos B \cos C-\cos (A+B+C)) \leq \frac{4}{9}
$$
The cosine function is concave down on $(0, \pi / 2)$. Therefore, if $\theta=\frac{A+B+C}{3}$, by the AM-GM inequality and Jensen's inequality,
$$
\cos A \cos B \cos C \leq\left(\frac{\cos A+\cos B+\cos C}{3}\right)^{3} \leq \cos ^{3} \frac{A+B+C}{3}=\cos ^{3} \theta
$$
Therefore, since $\cos A \cos B \cos C-\cos (A+B+C)=\sin A \sin B \cos C+\cos A \sin B \sin C+$ $\sin A \cos B \sin C>0$, and recalling that $\cos 3 \theta=4 \cos ^{3} \theta-3 \cos \theta$,
$\cos A \cos B \cos C(\cos A \cos B \cos C-\cos (A+B+C)) \leq \cos ^{3} \theta\left(\cos ^{3} \theta-\cos 3 \theta\right)=3 \cos ^{4} \theta\left(1-\cos ^{2} \theta\right)$. Finally, by AM-GM (notice that $1-\cos ^{2} \theta=\sin ^{2} \theta>0$ ),
$3 \cos ^{4} \theta\left(1-\cos ^{2} \theta\right)=\frac{3}{2} \cos ^{2} \theta \cdot \cos ^{2} \theta\left(2-2 \cos ^{2} \theta\right) \leq \frac{3}{2}\left(\frac{\cos ^{2} \theta+\cos ^{2} \theta+\left(2-2 \cos ^{2} \theta\right)}{3}\right)^{3}=\frac{4}{9}$,
and the result follows.
|
{
"resource_path": "APMO/segmented/en-apmo2004_sol.jsonl",
"problem_match": "# Problem 5",
"solution_match": "# Solution 3"
}
|
85c2e20c-c2c5-5955-a346-fe489616b284
| 604,886
|
Prove that for every irrational real number $a$, there are irrational real numbers $b$ and $b^{\prime}$ so that $a+b$ and $a b^{\prime}$ are both rational while $a b$ and $a+b^{\prime}$ are both irrational.
|
Let $a$ be an irrational number. If $a^{2}$ is irrational, we let $b=-a$. Then, $a+b=0$ is rational and $a b=-a^{2}$ is irrational. If $a^{2}$ is rational, we let $b=a^{2}-a$. Then, $a+b=a^{2}$ is rational and $a b=a^{2}(a-1)$. Since
$$
a=\frac{a b}{a^{2}}+1
$$
is irrational, so is $a b$.
Now, we let $b^{\prime}=\frac{1}{a}$ or $b^{\prime}=\frac{2}{a}$. Then $a b^{\prime}=1$ or 2 , which is rational. Note that
$$
a+b^{\prime}=\frac{a^{2}+1}{a} \quad \text { or } \quad a+b^{\prime}=\frac{a^{2}+2}{a} .
$$
Since,
$$
\frac{a^{2}+2}{a}-\frac{a^{2}+1}{a}=\frac{1}{a}
$$
at least one of them is irrational.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that for every irrational real number $a$, there are irrational real numbers $b$ and $b^{\prime}$ so that $a+b$ and $a b^{\prime}$ are both rational while $a b$ and $a+b^{\prime}$ are both irrational.
|
Let $a$ be an irrational number. If $a^{2}$ is irrational, we let $b=-a$. Then, $a+b=0$ is rational and $a b=-a^{2}$ is irrational. If $a^{2}$ is rational, we let $b=a^{2}-a$. Then, $a+b=a^{2}$ is rational and $a b=a^{2}(a-1)$. Since
$$
a=\frac{a b}{a^{2}}+1
$$
is irrational, so is $a b$.
Now, we let $b^{\prime}=\frac{1}{a}$ or $b^{\prime}=\frac{2}{a}$. Then $a b^{\prime}=1$ or 2 , which is rational. Note that
$$
a+b^{\prime}=\frac{a^{2}+1}{a} \quad \text { or } \quad a+b^{\prime}=\frac{a^{2}+2}{a} .
$$
Since,
$$
\frac{a^{2}+2}{a}-\frac{a^{2}+1}{a}=\frac{1}{a}
$$
at least one of them is irrational.
|
{
"resource_path": "APMO/segmented/en-apmo2005_sol.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "(Solution)"
}
|
197b3c87-50d9-56a2-8740-d7d83df5ffba
| 260,545
|
Let $a, b$ and $c$ be positive real numbers such that $a b c=8$. Prove that
$$
\frac{a^{2}}{\sqrt{\left(1+a^{3}\right)\left(1+b^{3}\right)}}+\frac{b^{2}}{\sqrt{\left(1+b^{3}\right)\left(1+c^{3}\right)}}+\frac{c^{2}}{\sqrt{\left(1+c^{3}\right)\left(1+a^{3}\right)}} \geq \frac{4}{3} .
$$
|
Observe that
$$
\frac{1}{\sqrt{1+x^{3}}} \geq \frac{2}{2+x^{2}}
$$
In fact, this is equivalent to $\left(2+x^{2}\right)^{2} \geq 4\left(1+x^{3}\right)$, or $x^{2}(x-2)^{2} \geq 0$. Notice that equality holds in (1) if and only if $x=2$.
We substitute $x$ by $a, b, c$ in (1), respectively, to find
$$
\begin{gathered}
\frac{a^{2}}{\sqrt{\left(1+a^{3}\right)\left(1+b^{3}\right)}}+\frac{b^{2}}{\sqrt{\left(1+b^{3}\right)\left(1+c^{3}\right)}}+\frac{c^{2}}{\sqrt{\left(1+c^{3}\right)\left(1+a^{3}\right)}} \\
\geq \frac{4 a^{2}}{\left(2+a^{2}\right)\left(2+b^{2}\right)}+\frac{4 b^{2}}{\left(2+b^{2}\right)\left(2+c^{2}\right)}+\frac{4 c^{2}}{\left(2+c^{2}\right)\left(2+a^{2}\right)}
\end{gathered}
$$
We combine the terms on the right hand side of (2) to obtain
$$
\text { Left hand side of }(2) \geq \frac{2 S(a, b, c)}{36+S(a, b, c)}=\frac{2}{1+36 / S(a, b, c)}
$$
where $S(a, b, c):=2\left(a^{2}+b^{2}+c^{2}\right)+(a b)^{2}+(b c)^{2}+(c a)^{2}$. By AM-GM inequality, we have
$$
\begin{aligned}
a^{2}+b^{2}+c^{2} & \geq 3 \sqrt[3]{(a b c)^{2}}=12 \\
(a b)^{2}+(b c)^{2}+(c a)^{2} & \geq 3 \sqrt[3]{(a b c)^{4}}=48
\end{aligned}
$$
Note that the equalities holds if and only if $a=b=c=2$. The above inequalities yield
$$
S(a, b, c)=2\left(a^{2}+b^{2}+c^{2}\right)+(a b)^{2}+(b c)^{2}+(c a)^{2} \geq 72
$$
Therefore
$$
\frac{2}{1+36 / S(a, b, c)} \geq \frac{2}{1+36 / 72}=\frac{4}{3}
$$
which is the required inequality.
|
\frac{4}{3}
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b$ and $c$ be positive real numbers such that $a b c=8$. Prove that
$$
\frac{a^{2}}{\sqrt{\left(1+a^{3}\right)\left(1+b^{3}\right)}}+\frac{b^{2}}{\sqrt{\left(1+b^{3}\right)\left(1+c^{3}\right)}}+\frac{c^{2}}{\sqrt{\left(1+c^{3}\right)\left(1+a^{3}\right)}} \geq \frac{4}{3} .
$$
|
Observe that
$$
\frac{1}{\sqrt{1+x^{3}}} \geq \frac{2}{2+x^{2}}
$$
In fact, this is equivalent to $\left(2+x^{2}\right)^{2} \geq 4\left(1+x^{3}\right)$, or $x^{2}(x-2)^{2} \geq 0$. Notice that equality holds in (1) if and only if $x=2$.
We substitute $x$ by $a, b, c$ in (1), respectively, to find
$$
\begin{gathered}
\frac{a^{2}}{\sqrt{\left(1+a^{3}\right)\left(1+b^{3}\right)}}+\frac{b^{2}}{\sqrt{\left(1+b^{3}\right)\left(1+c^{3}\right)}}+\frac{c^{2}}{\sqrt{\left(1+c^{3}\right)\left(1+a^{3}\right)}} \\
\geq \frac{4 a^{2}}{\left(2+a^{2}\right)\left(2+b^{2}\right)}+\frac{4 b^{2}}{\left(2+b^{2}\right)\left(2+c^{2}\right)}+\frac{4 c^{2}}{\left(2+c^{2}\right)\left(2+a^{2}\right)}
\end{gathered}
$$
We combine the terms on the right hand side of (2) to obtain
$$
\text { Left hand side of }(2) \geq \frac{2 S(a, b, c)}{36+S(a, b, c)}=\frac{2}{1+36 / S(a, b, c)}
$$
where $S(a, b, c):=2\left(a^{2}+b^{2}+c^{2}\right)+(a b)^{2}+(b c)^{2}+(c a)^{2}$. By AM-GM inequality, we have
$$
\begin{aligned}
a^{2}+b^{2}+c^{2} & \geq 3 \sqrt[3]{(a b c)^{2}}=12 \\
(a b)^{2}+(b c)^{2}+(c a)^{2} & \geq 3 \sqrt[3]{(a b c)^{4}}=48
\end{aligned}
$$
Note that the equalities holds if and only if $a=b=c=2$. The above inequalities yield
$$
S(a, b, c)=2\left(a^{2}+b^{2}+c^{2}\right)+(a b)^{2}+(b c)^{2}+(c a)^{2} \geq 72
$$
Therefore
$$
\frac{2}{1+36 / S(a, b, c)} \geq \frac{2}{1+36 / 72}=\frac{4}{3}
$$
which is the required inequality.
|
{
"resource_path": "APMO/segmented/en-apmo2005_sol.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "(Solution)"
}
|
dbae64fe-5924-5ac8-9bba-a107e5e4bc31
| 604,948
|
Prove that there exists a triangle which can be cut into 2005 congruent triangles.
|
Suppose that one side of a triangle has length $n$. Then it can be cut into $n^{2}$ congruent triangles which are similar to the original one and whose corresponding sides to the side of length $n$ have lengths 1 .
Since $2005=5 \times 401$ where 5 and 401 are primes and both primes are of the type $4 k+1$, it is representable as a sum of two integer squares. Indeed, it is easy to see that
$$
\begin{aligned}
2005 & =5 \times 401=\left(2^{2}+1\right)\left(20^{2}+1\right) \\
& =40^{2}+20^{2}+2^{2}+1 \\
& =(40-1)^{2}+2 \times 40+20^{2}+2^{2} \\
& =39^{2}+22^{2}
\end{aligned}
$$
Let $A B C$ be a right-angled triangle with the legs $A B$ and $B C$ having lengths 39 and 22 , respectively. We draw the altitude $B K$, which divides $A B C$ into two similar triangles. Now we divide $A B K$ into $39^{2}$ congruent triangles as described above and $B C K$ into $22^{2}$ congruent triangles. Since $A B K$ is similar to $B K C$, all 2005 triangles will be congruent.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Prove that there exists a triangle which can be cut into 2005 congruent triangles.
|
Suppose that one side of a triangle has length $n$. Then it can be cut into $n^{2}$ congruent triangles which are similar to the original one and whose corresponding sides to the side of length $n$ have lengths 1 .
Since $2005=5 \times 401$ where 5 and 401 are primes and both primes are of the type $4 k+1$, it is representable as a sum of two integer squares. Indeed, it is easy to see that
$$
\begin{aligned}
2005 & =5 \times 401=\left(2^{2}+1\right)\left(20^{2}+1\right) \\
& =40^{2}+20^{2}+2^{2}+1 \\
& =(40-1)^{2}+2 \times 40+20^{2}+2^{2} \\
& =39^{2}+22^{2}
\end{aligned}
$$
Let $A B C$ be a right-angled triangle with the legs $A B$ and $B C$ having lengths 39 and 22 , respectively. We draw the altitude $B K$, which divides $A B C$ into two similar triangles. Now we divide $A B K$ into $39^{2}$ congruent triangles as described above and $B C K$ into $22^{2}$ congruent triangles. Since $A B K$ is similar to $B K C$, all 2005 triangles will be congruent.
|
{
"resource_path": "APMO/segmented/en-apmo2005_sol.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "(Solution)"
}
|
b44bcc5e-7b01-51d5-b263-7753936a317f
| 55,289
|
In a small town, there are $n \times n$ houses indexed by $(i, j)$ for $1 \leq i, j \leq n$ with $(1,1)$ being the house at the top left corner, where $i$ and $j$ are the row and column indices, respectively. At time 0 , a fire breaks out at the house indexed by $(1, c)$, where $c \leq \frac{n}{2}$. During each subsequent time interval $[t, t+1]$, the fire fighters defend a house which is not yet on fire while the fire spreads to all undefended neighbors of each house which was on fire at time $t$. Once a house is defended, it remains so all the time. The process ends when the fire can no longer spread. At most how many houses can be saved by the fire fighters? A house indexed by $(i, j)$ is a neighbor of a house indexed by $(k, \ell)$ if $|i-k|+|j-\ell|=1$.
|
At most $n^{2}+c^{2}-n c-c$ houses can be saved. This can be achieved under the following order of defending:
$$
\begin{gathered}
(2, c),(2, c+1) ;(3, c-1),(3, c+2) ;(4, c-2),(4, c+3) ; \ldots \\
(c+1,1),(c+1,2 c) ;(c+1,2 c+1), \ldots,(c+1, n)
\end{gathered}
$$
Under this strategy, there are
2 columns (column numbers $c, c+1$ ) at which $n-1$ houses are saved
2 columns (column numbers $c-1, c+2$ ) at which $n-2$ houses are saved
...
2 columns (column numbers $1,2 c$ ) at which $n-c$ houses are saved
$n-2 c$ columns (column numbers $n-2 c+1, \ldots, n$ ) at which $n-c$ houses are saved
Adding all these we obtain :
$$
2[(n-1)+(n-2)+\cdots+(n-c)]+(n-2 c)(n-c)=n^{2}+c^{2}-c n-c
$$
We say that a house indexed by $(i, j)$ is at level $t$ if $|i-1|+|j-c|=t$. Let $d(t)$ be the number of houses at level $t$ defended by time $t$, and $p(t)$ be the number of houses at levels greater than $t$ defended by time $t$. It is clear that
$$
p(t)+\sum_{i=1}^{t} d(i) \leq t \text { and } p(t+1)+d(t+1) \leq p(t)+1
$$
Let $s(t)$ be the number of houses at level $t$ which are not burning at time $t$. We prove that
$$
s(t) \leq t-p(t) \leq t
$$
for $1 \leq t \leq n-1$ by induction. It is obvious when $t=1$. Assume that it is true for $t=k$. The union of the neighbors of any $k-p(k)+1$ houses at level $k+1$ contains at least $k-p(k)+1$ vertices at level $k$. Since $s(k) \leq k-p(k)$, one of these houses at level $k$ is burning. Therefore, at most $k-p(k)$ houses at level $k+1$ have no neighbor burning. Hence we have
$$
\begin{aligned}
s(k+1) & \leq k-p(k)+d(k+1) \\
& =(k+1)-(p(k)+1-d(k+1)) \\
& \leq(k+1)-p(k+1)
\end{aligned}
$$
We now prove that the strategy given above is optimal. Since
$$
\sum_{t=1}^{n-1} s(t) \leq\binom{ n}{2}
$$
the maximum number of houses at levels less than or equal to $n-1$, that can be saved under any strategy is at most $\binom{n}{2}$, which is realized by the strategy above. Moreover, at levels bigger than $n-1$, every house is saved under the strategy above.
The following is an example when $n=11$ and $c=4$. The houses with $\bigcirc$ mark are burned. The houses with $\otimes$ mark are blocked ones and hence those and the houses below them are saved.
|
n^{2}+c^{2}-n c-c
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In a small town, there are $n \times n$ houses indexed by $(i, j)$ for $1 \leq i, j \leq n$ with $(1,1)$ being the house at the top left corner, where $i$ and $j$ are the row and column indices, respectively. At time 0 , a fire breaks out at the house indexed by $(1, c)$, where $c \leq \frac{n}{2}$. During each subsequent time interval $[t, t+1]$, the fire fighters defend a house which is not yet on fire while the fire spreads to all undefended neighbors of each house which was on fire at time $t$. Once a house is defended, it remains so all the time. The process ends when the fire can no longer spread. At most how many houses can be saved by the fire fighters? A house indexed by $(i, j)$ is a neighbor of a house indexed by $(k, \ell)$ if $|i-k|+|j-\ell|=1$.
|
At most $n^{2}+c^{2}-n c-c$ houses can be saved. This can be achieved under the following order of defending:
$$
\begin{gathered}
(2, c),(2, c+1) ;(3, c-1),(3, c+2) ;(4, c-2),(4, c+3) ; \ldots \\
(c+1,1),(c+1,2 c) ;(c+1,2 c+1), \ldots,(c+1, n)
\end{gathered}
$$
Under this strategy, there are
2 columns (column numbers $c, c+1$ ) at which $n-1$ houses are saved
2 columns (column numbers $c-1, c+2$ ) at which $n-2$ houses are saved
...
2 columns (column numbers $1,2 c$ ) at which $n-c$ houses are saved
$n-2 c$ columns (column numbers $n-2 c+1, \ldots, n$ ) at which $n-c$ houses are saved
Adding all these we obtain :
$$
2[(n-1)+(n-2)+\cdots+(n-c)]+(n-2 c)(n-c)=n^{2}+c^{2}-c n-c
$$
We say that a house indexed by $(i, j)$ is at level $t$ if $|i-1|+|j-c|=t$. Let $d(t)$ be the number of houses at level $t$ defended by time $t$, and $p(t)$ be the number of houses at levels greater than $t$ defended by time $t$. It is clear that
$$
p(t)+\sum_{i=1}^{t} d(i) \leq t \text { and } p(t+1)+d(t+1) \leq p(t)+1
$$
Let $s(t)$ be the number of houses at level $t$ which are not burning at time $t$. We prove that
$$
s(t) \leq t-p(t) \leq t
$$
for $1 \leq t \leq n-1$ by induction. It is obvious when $t=1$. Assume that it is true for $t=k$. The union of the neighbors of any $k-p(k)+1$ houses at level $k+1$ contains at least $k-p(k)+1$ vertices at level $k$. Since $s(k) \leq k-p(k)$, one of these houses at level $k$ is burning. Therefore, at most $k-p(k)$ houses at level $k+1$ have no neighbor burning. Hence we have
$$
\begin{aligned}
s(k+1) & \leq k-p(k)+d(k+1) \\
& =(k+1)-(p(k)+1-d(k+1)) \\
& \leq(k+1)-p(k+1)
\end{aligned}
$$
We now prove that the strategy given above is optimal. Since
$$
\sum_{t=1}^{n-1} s(t) \leq\binom{ n}{2}
$$
the maximum number of houses at levels less than or equal to $n-1$, that can be saved under any strategy is at most $\binom{n}{2}$, which is realized by the strategy above. Moreover, at levels bigger than $n-1$, every house is saved under the strategy above.
The following is an example when $n=11$ and $c=4$. The houses with $\bigcirc$ mark are burned. The houses with $\otimes$ mark are blocked ones and hence those and the houses below them are saved.

|
{
"resource_path": "APMO/segmented/en-apmo2005_sol.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "(Solution)"
}
|
ab2e01d6-9893-55dd-a5ef-36ae08e81cdd
| 604,978
|
In a triangle $A B C$, points $M$ and $N$ are on sides $A B$ and $A C$, respectively, such that $M B=B C=C N$. Let $R$ and $r$ denote the circumradius and the inradius of the triangle $A B C$, respectively. Express the ratio $M N / B C$ in terms of $R$ and $r$.
|
Let $\omega, O$ and $I$ be the circumcircle, the circumcenter and the incenter of $A B C$, respectively. Let $D$ be the point of intersection of the line $B I$ and the circle $\omega$ such that $D \neq B$. Then $D$ is the midpoint of the arc $A C$. Hence $O D \perp C N$ and $O D=R$.
We first show that triangles $M N C$ and $I O D$ are similar. Because $B C=B M$, the line $B I$ (the bisector of $\angle M B C$ ) is perpendicular to the line $C M$. Because $O D \perp C N$ and $I D \perp M C$, it follows that
$$
\angle O D I=\angle N C M
$$
Let $\angle A B C=2 \beta$. In the triangle $B C M$, we have
$$
\frac{C M}{N C}=\frac{C M}{B C}=2 \sin \beta
$$
Since $\angle D I C=\angle D C I$, we have $I D=C D=A D$. Let $E$ be the point of intersection of the line $D O$ and the circle $\omega$ such that $E \neq D$. Then $D E$ is a diameter of $\omega$ and $\angle D E C=\angle D B C=\beta$. Thus we have
$$
\frac{D I}{O D}=\frac{C D}{O D}=\frac{2 R \sin \beta}{R}=2 \sin \beta .
$$
Combining equations (8), (9), and (10) shows that triangles $M N C$ and $I O D$ are similar. It follows that
$$
\frac{M N}{B C}=\frac{M N}{N C}=\frac{I O}{O D}=\frac{I O}{R} .
$$
The well-known Euler's formula states that
$$
O I^{2}=R^{2}-2 R r .
$$
Therefore,
$$
\frac{M N}{B C}=\sqrt{1-\frac{2 r}{R}}
$$
(Alternative Solution) Let $a$ (resp., $b, c$ ) be the length of $B C$ (resp., $A C, A B$ ). Let $\alpha$ (resp., $\beta, \gamma$ ) denote the angle $\angle B A C$ (resp., $\angle A B C, \angle A C B$ ). By introducing coordinates $B=(0,0), C=(a, 0)$, it is immediate that the coordinates of $M$ and $N$ are
$$
M=(a \cos \beta, a \sin \beta), \quad N=(a-a \cos \gamma, a \sin \gamma)
$$
respectively. Therefore,
$$
\begin{aligned}
(M N / B C)^{2} & =\left[(a-a \cos \gamma-a \cos \beta)^{2}+(a \sin \gamma-a \sin \beta)^{2}\right] / a^{2} \\
& =(1-\cos \gamma-\cos \beta)^{2}+(\sin \gamma-\sin \beta)^{2} \\
& =3-2 \cos \gamma-2 \cos \beta+2(\cos \gamma \cos \beta-\sin \gamma \sin \beta) \\
& =3-2 \cos \gamma-2 \cos \beta+2 \cos (\gamma+\beta) \\
& =3-2 \cos \gamma-2 \cos \beta-2 \cos \alpha \\
& =3-2(\cos \gamma+\cos \beta+\cos \alpha) .
\end{aligned}
$$
Now we claim
$$
\cos \gamma+\cos \beta+\cos \alpha=\frac{r}{R}+1
$$
From
$$
\begin{aligned}
& a=b \cos \gamma+c \cos \beta \\
& b=c \cos \alpha+a \cos \gamma \\
& c=a \cos \beta+b \cos \alpha
\end{aligned}
$$
we get
$$
a(1+\cos \alpha)+b(1+\cos \beta)+c(1+\cos \gamma)=(a+b+c)(\cos \alpha+\cos \beta+\cos \gamma)
$$
Thus
$$
\begin{aligned}
& \cos \alpha+\cos \beta+\cos \gamma \\
& =\frac{1}{a+b+c}(a(1+\cos \alpha)+b(1+\cos \beta)+c(1+\cos \gamma)) \\
& =\frac{1}{a+b+c}\left(a\left(1+\frac{b^{2}+c^{2}-a^{2}}{2 b c}\right)+b\left(1+\frac{a^{2}+c^{2}-b^{2}}{2 a c}\right)+c\left(1+\frac{a^{2}+b^{2}-c^{2}}{2 a b}\right)\right) \\
& =\frac{1}{a+b+c}\left(a+b+c+\frac{a^{2}\left(b^{2}+c^{2}-a^{2}\right)+b^{2}\left(a^{2}+c^{2}-b^{2}\right)+c^{2}\left(a^{2}+b^{2}-c^{2}\right)}{2 a b c}\right) \\
& =1+\frac{2 a^{2} b^{2}+2 b^{2} c^{2}+2 c^{2} a^{2}-a^{4}-b^{4}-c^{4}}{2 a b c(a+b+c)}
\end{aligned}
$$
On the other hand, from $R=\frac{a}{2 \sin \alpha}$ it follows that
$$
\begin{aligned}
R^{2} & =\frac{a^{2}}{4\left(1-\cos ^{2} \alpha\right)}=\frac{a^{2}}{4\left(1-\left(\frac{b^{2}+c^{2}-a^{2}}{2 b c}\right)^{2}\right)} \\
& =\frac{a^{2} b^{2} c^{2}}{2 a^{2} b^{2}+2 b^{2} c^{2}+2 c^{2} a^{2}-a^{4}-b^{4}-c^{4}}
\end{aligned}
$$
Also from $\frac{1}{2}(a+b+c) r=\frac{1}{2} b c \sin \alpha$, it follows that
$$
\begin{aligned}
r^{2} & =\frac{b^{2} c^{2}\left(1-\cos ^{2} \alpha\right)}{(a+b+c)^{2}}=\frac{b^{2} c^{2}\left(1-\left(\frac{b^{2}+c^{2}-a^{2}}{2 b c}\right)^{2}\right)}{(a+b+c)^{2}} \\
& =\frac{2 a^{2} b^{2}+2 b^{2} c^{2}+2 c^{2} a^{2}-a^{4}-b^{4}-c^{4}}{4(a+b+c)^{2}}
\end{aligned}
$$
Combining (19), (20) and (21), we get (16) as desired.
Finally, by (15) and (16) we have
$$
\frac{M N}{B C}=\sqrt{1-\frac{2 r}{R}}
$$
Another proof of (16) from R.A. Johnson's "Advanced Euclidean Geometry" ${ }^{1}$ :
Construct the perpendicular bisectors $O D, O E, O F$, where $D, E, F$ are the midpoints of $B C, C A, A B$, respectively. By Ptolemy's Theorem applied to the cyclic quadrilateral $O E A F$, we get
$$
\frac{a}{2} \cdot R=\frac{b}{2} \cdot O F+\frac{c}{2} \cdot O E
$$
Similarly
$$
\frac{b}{2} \cdot R=\frac{c}{2} \cdot O D+\frac{a}{2} \cdot O F, \quad \frac{c}{2} \cdot R=\frac{a}{2} \cdot O E+\frac{b}{2} \cdot O D .
$$
Adding, we get
$$
s R=O D \cdot \frac{b+c}{2}+O E \cdot \frac{c+a}{2}+O F \cdot \frac{a+b}{2}
$$
where $s$ is the semiperimeter. But also, the area of triangle $O B C$ is $O D \cdot \frac{a}{2}$, and adding similar formulas for the areas of triangles $O C A$ and $O A B$ gives
$$
r s=\triangle A B C=O D \cdot \frac{a}{2}+O E \cdot \frac{b}{2}+O F \cdot \frac{c}{2}
$$
Adding (23) and (24) gives $s(R+r)=s(O D+O E+O F)$, or
$$
O D+O E+O F=R+r .
$$
Since $O D=R \cos A$ etc., (16) follows.
[^0]
[^0]: ${ }^{1}$ This proof was introduced to the coordinating country by Professor Bill Sands of Canada.
|
\sqrt{1-\frac{2 r}{R}}
|
Yes
|
Incomplete
|
math-word-problem
|
Geometry
|
In a triangle $A B C$, points $M$ and $N$ are on sides $A B$ and $A C$, respectively, such that $M B=B C=C N$. Let $R$ and $r$ denote the circumradius and the inradius of the triangle $A B C$, respectively. Express the ratio $M N / B C$ in terms of $R$ and $r$.
|
Let $\omega, O$ and $I$ be the circumcircle, the circumcenter and the incenter of $A B C$, respectively. Let $D$ be the point of intersection of the line $B I$ and the circle $\omega$ such that $D \neq B$. Then $D$ is the midpoint of the arc $A C$. Hence $O D \perp C N$ and $O D=R$.
We first show that triangles $M N C$ and $I O D$ are similar. Because $B C=B M$, the line $B I$ (the bisector of $\angle M B C$ ) is perpendicular to the line $C M$. Because $O D \perp C N$ and $I D \perp M C$, it follows that
$$
\angle O D I=\angle N C M
$$
Let $\angle A B C=2 \beta$. In the triangle $B C M$, we have
$$
\frac{C M}{N C}=\frac{C M}{B C}=2 \sin \beta
$$
Since $\angle D I C=\angle D C I$, we have $I D=C D=A D$. Let $E$ be the point of intersection of the line $D O$ and the circle $\omega$ such that $E \neq D$. Then $D E$ is a diameter of $\omega$ and $\angle D E C=\angle D B C=\beta$. Thus we have
$$
\frac{D I}{O D}=\frac{C D}{O D}=\frac{2 R \sin \beta}{R}=2 \sin \beta .
$$
Combining equations (8), (9), and (10) shows that triangles $M N C$ and $I O D$ are similar. It follows that
$$
\frac{M N}{B C}=\frac{M N}{N C}=\frac{I O}{O D}=\frac{I O}{R} .
$$
The well-known Euler's formula states that
$$
O I^{2}=R^{2}-2 R r .
$$
Therefore,
$$
\frac{M N}{B C}=\sqrt{1-\frac{2 r}{R}}
$$
(Alternative Solution) Let $a$ (resp., $b, c$ ) be the length of $B C$ (resp., $A C, A B$ ). Let $\alpha$ (resp., $\beta, \gamma$ ) denote the angle $\angle B A C$ (resp., $\angle A B C, \angle A C B$ ). By introducing coordinates $B=(0,0), C=(a, 0)$, it is immediate that the coordinates of $M$ and $N$ are
$$
M=(a \cos \beta, a \sin \beta), \quad N=(a-a \cos \gamma, a \sin \gamma)
$$
respectively. Therefore,
$$
\begin{aligned}
(M N / B C)^{2} & =\left[(a-a \cos \gamma-a \cos \beta)^{2}+(a \sin \gamma-a \sin \beta)^{2}\right] / a^{2} \\
& =(1-\cos \gamma-\cos \beta)^{2}+(\sin \gamma-\sin \beta)^{2} \\
& =3-2 \cos \gamma-2 \cos \beta+2(\cos \gamma \cos \beta-\sin \gamma \sin \beta) \\
& =3-2 \cos \gamma-2 \cos \beta+2 \cos (\gamma+\beta) \\
& =3-2 \cos \gamma-2 \cos \beta-2 \cos \alpha \\
& =3-2(\cos \gamma+\cos \beta+\cos \alpha) .
\end{aligned}
$$
Now we claim
$$
\cos \gamma+\cos \beta+\cos \alpha=\frac{r}{R}+1
$$
From
$$
\begin{aligned}
& a=b \cos \gamma+c \cos \beta \\
& b=c \cos \alpha+a \cos \gamma \\
& c=a \cos \beta+b \cos \alpha
\end{aligned}
$$
we get
$$
a(1+\cos \alpha)+b(1+\cos \beta)+c(1+\cos \gamma)=(a+b+c)(\cos \alpha+\cos \beta+\cos \gamma)
$$
Thus
$$
\begin{aligned}
& \cos \alpha+\cos \beta+\cos \gamma \\
& =\frac{1}{a+b+c}(a(1+\cos \alpha)+b(1+\cos \beta)+c(1+\cos \gamma)) \\
& =\frac{1}{a+b+c}\left(a\left(1+\frac{b^{2}+c^{2}-a^{2}}{2 b c}\right)+b\left(1+\frac{a^{2}+c^{2}-b^{2}}{2 a c}\right)+c\left(1+\frac{a^{2}+b^{2}-c^{2}}{2 a b}\right)\right) \\
& =\frac{1}{a+b+c}\left(a+b+c+\frac{a^{2}\left(b^{2}+c^{2}-a^{2}\right)+b^{2}\left(a^{2}+c^{2}-b^{2}\right)+c^{2}\left(a^{2}+b^{2}-c^{2}\right)}{2 a b c}\right) \\
& =1+\frac{2 a^{2} b^{2}+2 b^{2} c^{2}+2 c^{2} a^{2}-a^{4}-b^{4}-c^{4}}{2 a b c(a+b+c)}
\end{aligned}
$$
On the other hand, from $R=\frac{a}{2 \sin \alpha}$ it follows that
$$
\begin{aligned}
R^{2} & =\frac{a^{2}}{4\left(1-\cos ^{2} \alpha\right)}=\frac{a^{2}}{4\left(1-\left(\frac{b^{2}+c^{2}-a^{2}}{2 b c}\right)^{2}\right)} \\
& =\frac{a^{2} b^{2} c^{2}}{2 a^{2} b^{2}+2 b^{2} c^{2}+2 c^{2} a^{2}-a^{4}-b^{4}-c^{4}}
\end{aligned}
$$
Also from $\frac{1}{2}(a+b+c) r=\frac{1}{2} b c \sin \alpha$, it follows that
$$
\begin{aligned}
r^{2} & =\frac{b^{2} c^{2}\left(1-\cos ^{2} \alpha\right)}{(a+b+c)^{2}}=\frac{b^{2} c^{2}\left(1-\left(\frac{b^{2}+c^{2}-a^{2}}{2 b c}\right)^{2}\right)}{(a+b+c)^{2}} \\
& =\frac{2 a^{2} b^{2}+2 b^{2} c^{2}+2 c^{2} a^{2}-a^{4}-b^{4}-c^{4}}{4(a+b+c)^{2}}
\end{aligned}
$$
Combining (19), (20) and (21), we get (16) as desired.
Finally, by (15) and (16) we have
$$
\frac{M N}{B C}=\sqrt{1-\frac{2 r}{R}}
$$
Another proof of (16) from R.A. Johnson's "Advanced Euclidean Geometry" ${ }^{1}$ :
Construct the perpendicular bisectors $O D, O E, O F$, where $D, E, F$ are the midpoints of $B C, C A, A B$, respectively. By Ptolemy's Theorem applied to the cyclic quadrilateral $O E A F$, we get
$$
\frac{a}{2} \cdot R=\frac{b}{2} \cdot O F+\frac{c}{2} \cdot O E
$$
Similarly
$$
\frac{b}{2} \cdot R=\frac{c}{2} \cdot O D+\frac{a}{2} \cdot O F, \quad \frac{c}{2} \cdot R=\frac{a}{2} \cdot O E+\frac{b}{2} \cdot O D .
$$
Adding, we get
$$
s R=O D \cdot \frac{b+c}{2}+O E \cdot \frac{c+a}{2}+O F \cdot \frac{a+b}{2}
$$
where $s$ is the semiperimeter. But also, the area of triangle $O B C$ is $O D \cdot \frac{a}{2}$, and adding similar formulas for the areas of triangles $O C A$ and $O A B$ gives
$$
r s=\triangle A B C=O D \cdot \frac{a}{2}+O E \cdot \frac{b}{2}+O F \cdot \frac{c}{2}
$$
Adding (23) and (24) gives $s(R+r)=s(O D+O E+O F)$, or
$$
O D+O E+O F=R+r .
$$
Since $O D=R \cos A$ etc., (16) follows.
[^0]
[^0]: ${ }^{1}$ This proof was introduced to the coordinating country by Professor Bill Sands of Canada.
|
{
"resource_path": "APMO/segmented/en-apmo2005_sol.jsonl",
"problem_match": "\nProblem 5.",
"solution_match": "(Solution)"
}
|
112e4a1b-8767-5f28-b737-304d1ad972d0
| 604,989
|
Let $n$ be a positive integer. Find the largest nonnegative real number $f(n)$ (depending on $n$ ) with the following property: whenever $a_{1}, a_{2}, \ldots, a_{n}$ are real numbers such that $a_{1}+a_{2}+\cdots+a_{n}$ is an integer, there exists some $i$ such that $\left|a_{i}-\frac{1}{2}\right| \geq f(n)$.
|
The answer is
$$
f(n)=\left\{\begin{array}{cl}
0 & \text { if } n \text { is even, } \\
\frac{1}{2 n} & \text { if } n \text { is odd. }
\end{array}\right.
$$
First, assume that $n$ is even. If $a_{i}=\frac{1}{2}$ for all $i$, then the sum $a_{1}+a_{2}+\cdots+a_{n}$ is an integer. Since $\left|a_{i}-\frac{1}{2}\right|=0$ for all $i$, we may conclude $f(n)=0$ for any even $n$.
Now assume that $n$ is odd. Suppose that $\left|a_{i}-\frac{1}{2}\right|<\frac{1}{2 n}$ for all $1 \leq i \leq n$. Then, since $\sum_{i=1}^{n} a_{i}$ is an integer,
$$
\frac{1}{2} \leq\left|\sum_{i=1}^{n} a_{i}-\frac{n}{2}\right| \leq \sum_{i=1}^{n}\left|a_{i}-\frac{1}{2}\right|<\frac{1}{2 n} \cdot n=\frac{1}{2}
$$
a contradiction. Thus $\left|a_{i}-\frac{1}{2}\right| \geq \frac{1}{2 n}$ for some $i$, as required. On the other hand, putting $n=2 m+1$ and $a_{i}=\frac{m}{2 m+1}$ for all $i$ gives $\sum a_{i}=m$, while
$$
\left|a_{i}-\frac{1}{2}\right|=\frac{1}{2}-\frac{m}{2 m+1}=\frac{1}{2(2 m+1)}=\frac{1}{2 n}
$$
for all $i$. Therefore, $f(n)=\frac{1}{2 n}$ is the best possible for any odd $n$.
|
f(n)=\left\{\begin{array}{cl}
0 & \text { if } n \text { is even, } \\
\frac{1}{2 n} & \text { if } n \text { is odd. }
\end{array}\right.}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $n$ be a positive integer. Find the largest nonnegative real number $f(n)$ (depending on $n$ ) with the following property: whenever $a_{1}, a_{2}, \ldots, a_{n}$ are real numbers such that $a_{1}+a_{2}+\cdots+a_{n}$ is an integer, there exists some $i$ such that $\left|a_{i}-\frac{1}{2}\right| \geq f(n)$.
|
The answer is
$$
f(n)=\left\{\begin{array}{cl}
0 & \text { if } n \text { is even, } \\
\frac{1}{2 n} & \text { if } n \text { is odd. }
\end{array}\right.
$$
First, assume that $n$ is even. If $a_{i}=\frac{1}{2}$ for all $i$, then the sum $a_{1}+a_{2}+\cdots+a_{n}$ is an integer. Since $\left|a_{i}-\frac{1}{2}\right|=0$ for all $i$, we may conclude $f(n)=0$ for any even $n$.
Now assume that $n$ is odd. Suppose that $\left|a_{i}-\frac{1}{2}\right|<\frac{1}{2 n}$ for all $1 \leq i \leq n$. Then, since $\sum_{i=1}^{n} a_{i}$ is an integer,
$$
\frac{1}{2} \leq\left|\sum_{i=1}^{n} a_{i}-\frac{n}{2}\right| \leq \sum_{i=1}^{n}\left|a_{i}-\frac{1}{2}\right|<\frac{1}{2 n} \cdot n=\frac{1}{2}
$$
a contradiction. Thus $\left|a_{i}-\frac{1}{2}\right| \geq \frac{1}{2 n}$ for some $i$, as required. On the other hand, putting $n=2 m+1$ and $a_{i}=\frac{m}{2 m+1}$ for all $i$ gives $\sum a_{i}=m$, while
$$
\left|a_{i}-\frac{1}{2}\right|=\frac{1}{2}-\frac{m}{2 m+1}=\frac{1}{2(2 m+1)}=\frac{1}{2 n}
$$
for all $i$. Therefore, $f(n)=\frac{1}{2 n}$ is the best possible for any odd $n$.
|
{
"resource_path": "APMO/segmented/en-apmo2006_sol.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "(Solution)"
}
|
b36d4a1c-e361-53e4-9edf-528c45aac04a
| 605,002
|
Prove that every positive integer can be written as a finite sum of distinct integral powers of the golden mean $\tau=\frac{1+\sqrt{5}}{2}$. Here, an integral power of $\tau$ is of the form $\tau^{i}$, where $i$ is an integer (not necessarily positive).
|
We will prove this statement by induction using the equality
$$
\tau^{2}=\tau+1
$$
If $n=1$, then $1=\tau^{0}$. Suppose that $n-1$ can be written as a finite sum of integral powers of $\tau$, say
$$
n-1=\sum_{i=-k}^{k} a_{i} \tau^{i}
$$
where $a_{i} \in\{0,1\}$ and $n \geq 2$. We will write (1) as
$$
n-1=a_{k} \cdots a_{1} a_{0} \cdot a_{-1} a_{-2} \cdots a_{-k}
$$
For example,
$$
1=1.0=0.11=0.1011=0.101011
$$
Firstly, we will prove that we may assume that in (2) we have $a_{i} a_{i+1}=0$ for all $i$ with $-k \leq i \leq k-1$. Indeed, if we have several occurrences of 11 , then we take the leftmost such occurrence. Since we may assume that it is preceded by a 0 , we can replace 011 with 100 using the identity $\tau^{i+1}+\tau^{i}=\tau^{i+2}$. By doing so repeatedly, if necessary, we will eliminate all occurrences of two 1's standing together. Now we have the representation
$$
n-1=\sum_{i=-K}^{K} b_{i} \tau^{i}
$$
where $b_{i} \in\{0,1\}$ and $b_{i} b_{i+1}=0$.
If $b_{0}=0$ in (3), then we just add $1=\tau^{0}$ to both sides of (3) and we are done.
Suppose now that there is 1 in the unit position of (3), that is $b_{0}=1$. If there are two 0 's to the right of it, i.e.
$$
n-1=\cdots 1.00 \cdots
$$
then we can replace 1.00 with 0.11 because $1=\tau^{-1}+\tau^{-2}$, and we are done because we obtain 0 in the unit position. Thus we may assume that
$$
n-1=\cdots 1.010 \cdots
$$
Again, if we have $n-1=\cdots 1.0100 \cdots$, we may rewrite it as
$$
n-1=\cdots 1.0100 \cdots=\cdots 1.0011 \cdots=\cdots 0.1111 \cdots
$$
and obtain 0 in the unit position. Therefore, we may assume that
$$
n-1=\cdots 1.01010 \cdots
$$
Since the number of 1's is finite, eventually we will obtain an occurrence of 100 at the end, i.e.
$$
n-1=\cdots 1.01010 \cdots 100
$$
Then we can shift all 1's to the right to obtain 0 in the unit position, i.e.
$$
n-1=\cdots 0.11 \cdots 11
$$
and we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that every positive integer can be written as a finite sum of distinct integral powers of the golden mean $\tau=\frac{1+\sqrt{5}}{2}$. Here, an integral power of $\tau$ is of the form $\tau^{i}$, where $i$ is an integer (not necessarily positive).
|
We will prove this statement by induction using the equality
$$
\tau^{2}=\tau+1
$$
If $n=1$, then $1=\tau^{0}$. Suppose that $n-1$ can be written as a finite sum of integral powers of $\tau$, say
$$
n-1=\sum_{i=-k}^{k} a_{i} \tau^{i}
$$
where $a_{i} \in\{0,1\}$ and $n \geq 2$. We will write (1) as
$$
n-1=a_{k} \cdots a_{1} a_{0} \cdot a_{-1} a_{-2} \cdots a_{-k}
$$
For example,
$$
1=1.0=0.11=0.1011=0.101011
$$
Firstly, we will prove that we may assume that in (2) we have $a_{i} a_{i+1}=0$ for all $i$ with $-k \leq i \leq k-1$. Indeed, if we have several occurrences of 11 , then we take the leftmost such occurrence. Since we may assume that it is preceded by a 0 , we can replace 011 with 100 using the identity $\tau^{i+1}+\tau^{i}=\tau^{i+2}$. By doing so repeatedly, if necessary, we will eliminate all occurrences of two 1's standing together. Now we have the representation
$$
n-1=\sum_{i=-K}^{K} b_{i} \tau^{i}
$$
where $b_{i} \in\{0,1\}$ and $b_{i} b_{i+1}=0$.
If $b_{0}=0$ in (3), then we just add $1=\tau^{0}$ to both sides of (3) and we are done.
Suppose now that there is 1 in the unit position of (3), that is $b_{0}=1$. If there are two 0 's to the right of it, i.e.
$$
n-1=\cdots 1.00 \cdots
$$
then we can replace 1.00 with 0.11 because $1=\tau^{-1}+\tau^{-2}$, and we are done because we obtain 0 in the unit position. Thus we may assume that
$$
n-1=\cdots 1.010 \cdots
$$
Again, if we have $n-1=\cdots 1.0100 \cdots$, we may rewrite it as
$$
n-1=\cdots 1.0100 \cdots=\cdots 1.0011 \cdots=\cdots 0.1111 \cdots
$$
and obtain 0 in the unit position. Therefore, we may assume that
$$
n-1=\cdots 1.01010 \cdots
$$
Since the number of 1's is finite, eventually we will obtain an occurrence of 100 at the end, i.e.
$$
n-1=\cdots 1.01010 \cdots 100
$$
Then we can shift all 1's to the right to obtain 0 in the unit position, i.e.
$$
n-1=\cdots 0.11 \cdots 11
$$
and we are done.
|
{
"resource_path": "APMO/segmented/en-apmo2006_sol.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "(Solution)"
}
|
2c596044-e4f8-5e79-a5e6-6136742a352d
| 261,486
|
Let $p \geq 5$ be a prime and let $r$ be the number of ways of placing $p$ checkers on a $p \times p$ checkerboard so that not all checkers are in the same row (but they may all be in the same column). Show that $r$ is divisible by $p^{5}$. Here, we assume that all the checkers are identical.
|
Note that $r=\binom{p^{2}}{p}-p$. Hence, it suffices to show that
$$
\left(p^{2}-1\right)\left(p^{2}-2\right) \cdots\left(p^{2}-(p-1)\right)-(p-1)!\equiv 0 \quad\left(\bmod p^{4}\right)
$$
Now, let
$$
f(x):=(x-1)(x-2) \cdots(x-(p-1))=x^{p-1}+s_{p-2} x^{p-2}+\cdots+s_{1} x+s_{0} .
$$
Then the congruence equation (1) is same as $f\left(p^{2}\right)-s_{0} \equiv 0\left(\bmod p^{4}\right)$. Therefore, it suffices to show that $s_{1} p^{2} \equiv 0\left(\bmod p^{4}\right)$ or $s_{1} \equiv 0\left(\bmod p^{2}\right)$.
Since $a^{p-1} \equiv 1(\bmod p)$ for all $1 \leq a \leq p-1$, we can factor
$$
x^{p-1}-1 \equiv(x-1)(x-2) \cdots(x-(p-1)) \quad(\bmod p)
$$
Comparing the coefficients of the left hand side of (3) with those of the right hand side of (2), we obtain $p \mid s_{i}$ for all $1 \leq i \leq p-2$ and $s_{0} \equiv-1(\bmod p)$. On the other hand, plugging $p$ for $x$ in (2), we get
$$
f(p)=(p-1)!=s_{0}=p^{p-1}+s_{p-2} p^{p-2}+\cdots+s_{1} p+s_{0}
$$
which implies
$$
p^{p-1}+s_{p-2} p^{p-2}+\cdots+s_{2} p^{2}=-s_{1} p
$$
Since $p \geq 5, p \mid s_{2}$ and hence $s_{1} \equiv 0\left(\bmod p^{2}\right)$ as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $p \geq 5$ be a prime and let $r$ be the number of ways of placing $p$ checkers on a $p \times p$ checkerboard so that not all checkers are in the same row (but they may all be in the same column). Show that $r$ is divisible by $p^{5}$. Here, we assume that all the checkers are identical.
|
Note that $r=\binom{p^{2}}{p}-p$. Hence, it suffices to show that
$$
\left(p^{2}-1\right)\left(p^{2}-2\right) \cdots\left(p^{2}-(p-1)\right)-(p-1)!\equiv 0 \quad\left(\bmod p^{4}\right)
$$
Now, let
$$
f(x):=(x-1)(x-2) \cdots(x-(p-1))=x^{p-1}+s_{p-2} x^{p-2}+\cdots+s_{1} x+s_{0} .
$$
Then the congruence equation (1) is same as $f\left(p^{2}\right)-s_{0} \equiv 0\left(\bmod p^{4}\right)$. Therefore, it suffices to show that $s_{1} p^{2} \equiv 0\left(\bmod p^{4}\right)$ or $s_{1} \equiv 0\left(\bmod p^{2}\right)$.
Since $a^{p-1} \equiv 1(\bmod p)$ for all $1 \leq a \leq p-1$, we can factor
$$
x^{p-1}-1 \equiv(x-1)(x-2) \cdots(x-(p-1)) \quad(\bmod p)
$$
Comparing the coefficients of the left hand side of (3) with those of the right hand side of (2), we obtain $p \mid s_{i}$ for all $1 \leq i \leq p-2$ and $s_{0} \equiv-1(\bmod p)$. On the other hand, plugging $p$ for $x$ in (2), we get
$$
f(p)=(p-1)!=s_{0}=p^{p-1}+s_{p-2} p^{p-2}+\cdots+s_{1} p+s_{0}
$$
which implies
$$
p^{p-1}+s_{p-2} p^{p-2}+\cdots+s_{2} p^{2}=-s_{1} p
$$
Since $p \geq 5, p \mid s_{2}$ and hence $s_{1} \equiv 0\left(\bmod p^{2}\right)$ as desired.
|
{
"resource_path": "APMO/segmented/en-apmo2006_sol.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "(Solution)"
}
|
440e1b89-c0aa-59a4-b99a-ecabe3f3d54a
| 261,496
|
Let $A, B$ be two distinct points on a given circle $O$ and let $P$ be the midpoint of the line segment $A B$. Let $O_{1}$ be the circle tangent to the line $A B$ at $P$ and tangent to the circle $O$. Let $\ell$ be the tangent line, different from the line $A B$, to $O_{1}$ passing through $A$. Let $C$ be the intersection point, different from $A$, of $\ell$ and $O$. Let $Q$ be the midpoint of the line segment $B C$ and $O_{2}$ be the circle tangent to the line $B C$ at $Q$ and tangent to the line segment $A C$. Prove that the circle $O_{2}$ is tangent to the circle $O$.
|
Let $S$ be the tangent point of the circles $O$ and $O_{1}$ and let $T$ be the intersection point, different from $S$, of the circle $O$ and the line $S P$. Let $X$ be the tangent point of $\ell$ to $O_{1}$ and let $M$ be the midpoint of the line segment $X P$. Since $\angle T B P=\angle A S P$, the triangle $T B P$ is similar to the triangle $A S P$. Therefore,
$$
\frac{P T}{P B}=\frac{P A}{P S}
$$
Since the line $\ell$ is tangent to the circle $O_{1}$ at $X$, we have
$$
\angle S P X=90^{\circ}-\angle X S P=90^{\circ}-\angle A P M=\angle P A M
$$
which implies that the triangle $P A M$ is similar to the triangle $S P X$. Consequently,
$$
\frac{X S}{X P}=\frac{M P}{M A}=\frac{X P}{2 M A} \quad \text { and } \quad \frac{X P}{P S}=\frac{M A}{A P}
$$
From this and the above observation follows
$$
\frac{X S}{X P} \cdot \frac{P T}{P B}=\frac{X P}{2 M A} \cdot \frac{P A}{P S}=\frac{X P}{2 M A} \cdot \frac{M A}{X P}=\frac{1}{2} .
$$
Let $A^{\prime}$ be the intersection point of the circle $O$ and the perpendicular bisector of the chord $B C$ such that $A, A^{\prime}$ are on the same side of the line $B C$, and $N$ be the intersection point of the lines $A^{\prime} Q$ and $C T$. Since
$$
\angle N C Q=\angle T C B=\angle T C A=\angle T B A=\angle T B P
$$
and
$$
\angle C A^{\prime} Q=\frac{\angle C A B}{2}=\frac{\angle X A P}{2}=\angle P A M=\angle S P X,
$$
the triangle $N C Q$ is similar to the triangle $T B P$ and the triangle $C A^{\prime} Q$ is similar to the triangle $S P X$. Therefore
$$
\frac{Q N}{Q C}=\frac{P T}{P B} \quad \text { and } \quad \frac{Q C}{Q A^{\prime}}=\frac{X S}{X P} .
$$
and hence $Q A^{\prime}=2 Q N$ by (1). This implies that $N$ is the midpoint of the line segment $Q A^{\prime}$. Let the circle $O_{2}$ touch the line segment $A C$ at $Y$. Since
$$
\angle A C N=\angle A C T=\angle B C T=\angle Q C N
$$
and $|C Y|=|C Q|$, the triangles $Y C N$ and $Q C N$ are congruent and hence $N Y \perp A C$ and $N Y=N Q=N A^{\prime}$. Therefore, $N$ is the center of the circle $O_{2}$, which completes the proof.
Remark: Analytic solutions are possible: For example, one can prove for a triangle $A B C$ inscribed in a circle $O$ that $A B=k(2+2 t), A C=k(1+2 t), B C=k(1+4 t)$ for some positive numbers $k, t$ if and only if there exists a circle $O_{1}$ such that $O_{1}$ is tangent to the side $A B$ at its midpoint, the side $A C$ and the circle $O$.
One obtains $A B=k^{\prime}\left(1+4 t^{\prime}\right), A C=k^{\prime}\left(1+2 t^{\prime}\right), B C=k^{\prime}\left(2+2 t^{\prime}\right)$ by substituting $t=1 / 4 t^{\prime}$ and $k=2 k^{\prime} t^{\prime}$. So, there exists a circle $O_{2}$ such that $O_{2}$ is tangent to the side $B C$ at its midpoint, the side $A C$ and the circle $O$.
In the above, $t=\tan ^{2} \alpha$ and $k=\frac{4 R \tan \alpha}{\left(1+\tan ^{2} \alpha\right)\left(1+4 \tan ^{2} \alpha\right)}$, where $R$ is the radius of $O$ and $\angle A=2 \alpha$. Furthermore, $t^{\prime}=\tan ^{2} \gamma$ and $k^{\prime}=\frac{4 R \tan \gamma}{\left(1+\tan ^{2} \gamma\right)\left(1+4 \tan ^{2} \gamma\right)}$, where $\angle C=2 \gamma$. Observe that $\sqrt{t t^{\prime}}=\tan \alpha \cdot \tan \gamma=\frac{X S}{X P} \cdot \frac{P T}{P B}=\frac{1}{2}$, which implies $t t^{\prime}=\frac{1}{4}$. It is now routine easy to check that $k=2 k^{\prime} t^{\prime}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A, B$ be two distinct points on a given circle $O$ and let $P$ be the midpoint of the line segment $A B$. Let $O_{1}$ be the circle tangent to the line $A B$ at $P$ and tangent to the circle $O$. Let $\ell$ be the tangent line, different from the line $A B$, to $O_{1}$ passing through $A$. Let $C$ be the intersection point, different from $A$, of $\ell$ and $O$. Let $Q$ be the midpoint of the line segment $B C$ and $O_{2}$ be the circle tangent to the line $B C$ at $Q$ and tangent to the line segment $A C$. Prove that the circle $O_{2}$ is tangent to the circle $O$.
|
Let $S$ be the tangent point of the circles $O$ and $O_{1}$ and let $T$ be the intersection point, different from $S$, of the circle $O$ and the line $S P$. Let $X$ be the tangent point of $\ell$ to $O_{1}$ and let $M$ be the midpoint of the line segment $X P$. Since $\angle T B P=\angle A S P$, the triangle $T B P$ is similar to the triangle $A S P$. Therefore,
$$
\frac{P T}{P B}=\frac{P A}{P S}
$$
Since the line $\ell$ is tangent to the circle $O_{1}$ at $X$, we have
$$
\angle S P X=90^{\circ}-\angle X S P=90^{\circ}-\angle A P M=\angle P A M
$$
which implies that the triangle $P A M$ is similar to the triangle $S P X$. Consequently,
$$
\frac{X S}{X P}=\frac{M P}{M A}=\frac{X P}{2 M A} \quad \text { and } \quad \frac{X P}{P S}=\frac{M A}{A P}
$$
From this and the above observation follows
$$
\frac{X S}{X P} \cdot \frac{P T}{P B}=\frac{X P}{2 M A} \cdot \frac{P A}{P S}=\frac{X P}{2 M A} \cdot \frac{M A}{X P}=\frac{1}{2} .
$$
Let $A^{\prime}$ be the intersection point of the circle $O$ and the perpendicular bisector of the chord $B C$ such that $A, A^{\prime}$ are on the same side of the line $B C$, and $N$ be the intersection point of the lines $A^{\prime} Q$ and $C T$. Since
$$
\angle N C Q=\angle T C B=\angle T C A=\angle T B A=\angle T B P
$$
and
$$
\angle C A^{\prime} Q=\frac{\angle C A B}{2}=\frac{\angle X A P}{2}=\angle P A M=\angle S P X,
$$
the triangle $N C Q$ is similar to the triangle $T B P$ and the triangle $C A^{\prime} Q$ is similar to the triangle $S P X$. Therefore
$$
\frac{Q N}{Q C}=\frac{P T}{P B} \quad \text { and } \quad \frac{Q C}{Q A^{\prime}}=\frac{X S}{X P} .
$$
and hence $Q A^{\prime}=2 Q N$ by (1). This implies that $N$ is the midpoint of the line segment $Q A^{\prime}$. Let the circle $O_{2}$ touch the line segment $A C$ at $Y$. Since
$$
\angle A C N=\angle A C T=\angle B C T=\angle Q C N
$$
and $|C Y|=|C Q|$, the triangles $Y C N$ and $Q C N$ are congruent and hence $N Y \perp A C$ and $N Y=N Q=N A^{\prime}$. Therefore, $N$ is the center of the circle $O_{2}$, which completes the proof.
Remark: Analytic solutions are possible: For example, one can prove for a triangle $A B C$ inscribed in a circle $O$ that $A B=k(2+2 t), A C=k(1+2 t), B C=k(1+4 t)$ for some positive numbers $k, t$ if and only if there exists a circle $O_{1}$ such that $O_{1}$ is tangent to the side $A B$ at its midpoint, the side $A C$ and the circle $O$.
One obtains $A B=k^{\prime}\left(1+4 t^{\prime}\right), A C=k^{\prime}\left(1+2 t^{\prime}\right), B C=k^{\prime}\left(2+2 t^{\prime}\right)$ by substituting $t=1 / 4 t^{\prime}$ and $k=2 k^{\prime} t^{\prime}$. So, there exists a circle $O_{2}$ such that $O_{2}$ is tangent to the side $B C$ at its midpoint, the side $A C$ and the circle $O$.
In the above, $t=\tan ^{2} \alpha$ and $k=\frac{4 R \tan \alpha}{\left(1+\tan ^{2} \alpha\right)\left(1+4 \tan ^{2} \alpha\right)}$, where $R$ is the radius of $O$ and $\angle A=2 \alpha$. Furthermore, $t^{\prime}=\tan ^{2} \gamma$ and $k^{\prime}=\frac{4 R \tan \gamma}{\left(1+\tan ^{2} \gamma\right)\left(1+4 \tan ^{2} \gamma\right)}$, where $\angle C=2 \gamma$. Observe that $\sqrt{t t^{\prime}}=\tan \alpha \cdot \tan \gamma=\frac{X S}{X P} \cdot \frac{P T}{P B}=\frac{1}{2}$, which implies $t t^{\prime}=\frac{1}{4}$. It is now routine easy to check that $k=2 k^{\prime} t^{\prime}$.
|
{
"resource_path": "APMO/segmented/en-apmo2006_sol.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "(Solution)"
}
|
311403b9-0e44-541c-b940-2241ae909e73
| 261,504
|
In a circus, there are $n$ clowns who dress and paint themselves up using a selection of 12 distinct colours. Each clown is required to use at least five different colours. One day, the ringmaster of the circus orders that no two clowns have exactly the same set
of colours and no more than 20 clowns may use any one particular colour. Find the largest number $n$ of clowns so as to make the ringmaster's order possible.
|
Let $C$ be the set of $n$ clowns. Label the colours $1,2,3, \ldots, 12$. For each $i=1,2, \ldots, 12$, let $E_{i}$ denote the set of clowns who use colour $i$. For each subset $S$ of $\{1,2, \ldots, 12\}$, let $E_{S}$ be the set of clowns who use exactly those colours in $S$. Since $S \neq S^{\prime}$ implies $E_{S} \cap E_{S^{\prime}}=\emptyset$, we have
$$
\sum_{S}\left|E_{S}\right|=|C|=n
$$
where $S$ runs over all subsets of $\{1,2, \ldots, 12\}$. Now for each $i$,
$$
E_{S} \subseteq E_{i} \quad \text { if and only if } \quad i \in S
$$
and hence
$$
\left|E_{i}\right|=\sum_{i \in S}\left|E_{S}\right|
$$
By assumption, we know that $\left|E_{i}\right| \leq 20$ and that if $E_{S} \neq \emptyset$, then $|S| \geq 5$. From this we obtain
$$
20 \times 12 \geq \sum_{i=1}^{12}\left|E_{i}\right|=\sum_{i=1}^{12}\left(\sum_{i \in S}\left|E_{S}\right|\right) \geq 5 \sum_{S}\left|E_{S}\right|=5 n
$$
Therefore $n \leq 48$.
Now, define a sequence $\left\{c_{i}\right\}_{i=1}^{52}$ of colours in the following way:
$1234|5678| 9101112 \mid$
$4123|8567| 1291011 \mid$
$3412|7856| 1112910 \mid$
$2341|6785| 1011129 \mid 1234$
The first row lists $c_{1}, \ldots, c_{12}$ in order, the second row lists $c_{13}, \ldots, c_{24}$ in order, the third row lists $c_{25}, \ldots, c_{36}$ in order, and finally the last row lists $c_{37}, \ldots, c_{52}$ in order. For each $j, 1 \leq j \leq 48$, assign colours $c_{j}, c_{j+1}, c_{j+2}, c_{j+3}, c_{j+4}$ to the $j$-th clown. It is easy to check that this assignment satisfies all conditions given above. So, 48 is the largest for $n$.
Remark: The fact that $n \leq 48$ can be obtained in a much simpler observation that
$$
5 n \leq 12 \times 20=240
$$
There are many other ways of constructing 48 distinct sets consisting of 5 colours. For example, consider the sets
$$
\begin{array}{cccc}
\{1,2,3,4,5,6\}, & \{3,4,5,6,7,8\}, & \{5,6,7,8,9,10\}, & \{7,8,9,10,11,12\}, \\
\{9,10,11,12,1,2\}, & \{11,12,1,2,3,4\}, & \{1,2,5,6,9,10\}, & \{3,4,7,8,11,12\} .
\end{array}
$$
Each of the above 8 sets has 6 distinct subsets consisting of exactly 5 colours. It is easy to check that the 48 subsets obtained in this manner are all distinct.
|
48
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In a circus, there are $n$ clowns who dress and paint themselves up using a selection of 12 distinct colours. Each clown is required to use at least five different colours. One day, the ringmaster of the circus orders that no two clowns have exactly the same set
of colours and no more than 20 clowns may use any one particular colour. Find the largest number $n$ of clowns so as to make the ringmaster's order possible.
|
Let $C$ be the set of $n$ clowns. Label the colours $1,2,3, \ldots, 12$. For each $i=1,2, \ldots, 12$, let $E_{i}$ denote the set of clowns who use colour $i$. For each subset $S$ of $\{1,2, \ldots, 12\}$, let $E_{S}$ be the set of clowns who use exactly those colours in $S$. Since $S \neq S^{\prime}$ implies $E_{S} \cap E_{S^{\prime}}=\emptyset$, we have
$$
\sum_{S}\left|E_{S}\right|=|C|=n
$$
where $S$ runs over all subsets of $\{1,2, \ldots, 12\}$. Now for each $i$,
$$
E_{S} \subseteq E_{i} \quad \text { if and only if } \quad i \in S
$$
and hence
$$
\left|E_{i}\right|=\sum_{i \in S}\left|E_{S}\right|
$$
By assumption, we know that $\left|E_{i}\right| \leq 20$ and that if $E_{S} \neq \emptyset$, then $|S| \geq 5$. From this we obtain
$$
20 \times 12 \geq \sum_{i=1}^{12}\left|E_{i}\right|=\sum_{i=1}^{12}\left(\sum_{i \in S}\left|E_{S}\right|\right) \geq 5 \sum_{S}\left|E_{S}\right|=5 n
$$
Therefore $n \leq 48$.
Now, define a sequence $\left\{c_{i}\right\}_{i=1}^{52}$ of colours in the following way:
$1234|5678| 9101112 \mid$
$4123|8567| 1291011 \mid$
$3412|7856| 1112910 \mid$
$2341|6785| 1011129 \mid 1234$
The first row lists $c_{1}, \ldots, c_{12}$ in order, the second row lists $c_{13}, \ldots, c_{24}$ in order, the third row lists $c_{25}, \ldots, c_{36}$ in order, and finally the last row lists $c_{37}, \ldots, c_{52}$ in order. For each $j, 1 \leq j \leq 48$, assign colours $c_{j}, c_{j+1}, c_{j+2}, c_{j+3}, c_{j+4}$ to the $j$-th clown. It is easy to check that this assignment satisfies all conditions given above. So, 48 is the largest for $n$.
Remark: The fact that $n \leq 48$ can be obtained in a much simpler observation that
$$
5 n \leq 12 \times 20=240
$$
There are many other ways of constructing 48 distinct sets consisting of 5 colours. For example, consider the sets
$$
\begin{array}{cccc}
\{1,2,3,4,5,6\}, & \{3,4,5,6,7,8\}, & \{5,6,7,8,9,10\}, & \{7,8,9,10,11,12\}, \\
\{9,10,11,12,1,2\}, & \{11,12,1,2,3,4\}, & \{1,2,5,6,9,10\}, & \{3,4,7,8,11,12\} .
\end{array}
$$
Each of the above 8 sets has 6 distinct subsets consisting of exactly 5 colours. It is easy to check that the 48 subsets obtained in this manner are all distinct.
|
{
"resource_path": "APMO/segmented/en-apmo2006_sol.jsonl",
"problem_match": "\nProblem 5.",
"solution_match": "(Solution)"
}
|
5b2a8169-c2ad-5a85-9550-581891fe4e37
| 261,512
|
Let $S$ be a set of 9 distinct integers all of whose prime factors are at most 3. Prove that $S$ contains 3 distinct integers such that their product is a perfect cube.
|
Without loss of generality, we may assume that $S$ contains only positive integers. Let
$$
S=\left\{2^{a_{i}} 3^{b_{i}} \mid a_{i}, b_{i} \in \mathbb{Z}, a_{i}, b_{i} \geq 0,1 \leq i \leq 9\right\}
$$
It suffices to show that there are $1 \leq i_{1}, i_{2}, i_{3} \leq 9$ such that
$$
a_{i_{1}}+a_{i_{2}}+a_{i_{3}} \equiv b_{i_{1}}+b_{i_{2}}+b_{i_{3}} \equiv 0 \quad(\bmod 3) .
$$
For $n=2^{a} 3^{b} \in S$, let's call $(a(\bmod 3), b(\bmod 3))$ the type of $n$. Then there are 9 possible types:
$$
(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2)
$$
Let $N(i, j)$ be the number of integers in $S$ of type $(i, j)$. We obtain 3 distinct integers whose product is a perfect cube when
(1) $N(i, j) \geq 3$ for some $i, j$, or
(2) $N(i, 0) N(i, 1) N(i, 2) \neq 0$ for some $i=0,1,2$, or
(3) $N(0, j) N(1, j) N(2, j) \neq 0$ for some $j=0,1,2$, or
(4) $N\left(i_{1}, j_{1}\right) N\left(i_{2}, j_{2}\right) N\left(i_{3}, j_{3}\right) \neq 0$, where $\left\{i_{1}, i_{2}, i_{3}\right\}=\left\{j_{1}, j_{2}, j_{3}\right\}=\{0,1,2\}$.
Assume that none of the conditions (1) (3) holds. Since $N(i, j) \leq 2$ for all $(i, j)$, there are at least five $N(i, j)$ 's that are nonzero. Furthermore, among those nonzero $N(i, j)$ 's, no three have the same $i$ nor the same $j$. Using these facts, one may easily conclude that the condition (4) should hold. (For example, if one places each nonzero $N(i, j)$ in the $(i, j)$-th box of a regular $3 \times 3$ array of boxes whose rows and columns are indexed by 0,1 and 2 , then one can always find three boxes, occupied by at least one nonzero $N(i, j)$, whose rows and columns are all distinct. This implies (4).)
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $S$ be a set of 9 distinct integers all of whose prime factors are at most 3. Prove that $S$ contains 3 distinct integers such that their product is a perfect cube.
|
Without loss of generality, we may assume that $S$ contains only positive integers. Let
$$
S=\left\{2^{a_{i}} 3^{b_{i}} \mid a_{i}, b_{i} \in \mathbb{Z}, a_{i}, b_{i} \geq 0,1 \leq i \leq 9\right\}
$$
It suffices to show that there are $1 \leq i_{1}, i_{2}, i_{3} \leq 9$ such that
$$
a_{i_{1}}+a_{i_{2}}+a_{i_{3}} \equiv b_{i_{1}}+b_{i_{2}}+b_{i_{3}} \equiv 0 \quad(\bmod 3) .
$$
For $n=2^{a} 3^{b} \in S$, let's call $(a(\bmod 3), b(\bmod 3))$ the type of $n$. Then there are 9 possible types:
$$
(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2)
$$
Let $N(i, j)$ be the number of integers in $S$ of type $(i, j)$. We obtain 3 distinct integers whose product is a perfect cube when
(1) $N(i, j) \geq 3$ for some $i, j$, or
(2) $N(i, 0) N(i, 1) N(i, 2) \neq 0$ for some $i=0,1,2$, or
(3) $N(0, j) N(1, j) N(2, j) \neq 0$ for some $j=0,1,2$, or
(4) $N\left(i_{1}, j_{1}\right) N\left(i_{2}, j_{2}\right) N\left(i_{3}, j_{3}\right) \neq 0$, where $\left\{i_{1}, i_{2}, i_{3}\right\}=\left\{j_{1}, j_{2}, j_{3}\right\}=\{0,1,2\}$.
Assume that none of the conditions (1) (3) holds. Since $N(i, j) \leq 2$ for all $(i, j)$, there are at least five $N(i, j)$ 's that are nonzero. Furthermore, among those nonzero $N(i, j)$ 's, no three have the same $i$ nor the same $j$. Using these facts, one may easily conclude that the condition (4) should hold. (For example, if one places each nonzero $N(i, j)$ in the $(i, j)$-th box of a regular $3 \times 3$ array of boxes whose rows and columns are indexed by 0,1 and 2 , then one can always find three boxes, occupied by at least one nonzero $N(i, j)$, whose rows and columns are all distinct. This implies (4).)
|
{
"resource_path": "APMO/segmented/en-apmo2007_sol.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution."
}
|
cb1a75c0-029c-534e-9491-d72a61bf40f2
| 605,094
|
Let $S$ be a set of 9 distinct integers all of whose prime factors are at most 3. Prove that $S$ contains 3 distinct integers such that their product is a perfect cube.
|
Up to $(\dagger)$, we do the same as above and get 9 possible types:
$$
(a(\bmod 3), b(\bmod 3))=(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2)
$$
for $n=2^{a} 3^{b} \in S$.
Note that (i) among any 5 integers, there exist 3 whose sum is $0(\bmod 3)$, and that (ii) if $i, j, k \in\{0,1,2\}$, then $i+j+k \equiv 0(\bmod 3)$ if and only if $i=j=k$ or $\{i, j, k\}=\{0,1,2\}$.
Let's define
$T$ : the set of types of the integers in $S$;
$N(i)$ : the number of integers in $S$ of the type $(i, \cdot)$;
$M(i)$ : the number of integers $j \in\{0,1,2\}$ such that $(i, j) \in T$.
If $N(i) \geq 5$ for some $i$, the result follows from (i). Otherwise, for some permutation $(i, j, k)$ of $(0,1,2)$,
$$
N(i) \geq 3, \quad N(j) \geq 3, \quad N(k) \geq 1
$$
If $M(i)$ or $M(j)$ is 1 or 3 , the result follows from (ii). Otherwise $M(i)=M(j)=2$. Then either
$$
(i, x),(i, y),(j, x),(j, y) \in T \quad \text { or } \quad(i, x),(i, y),(j, x),(j, z) \in T
$$
for some permutation $(x, y, z)$ of $(0,1,2)$. Since $N(k) \geq 1$, at least one of $(k, x),(k, y)$ and $(k, z)$ contained in $T$. Therefore, in any case, the result follows from (ii). (For example, if $(k, y) \in T$, then take $(i, y),(j, y),(k, y)$ or $(i, x),(j, z),(k, y)$ from T.)
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $S$ be a set of 9 distinct integers all of whose prime factors are at most 3. Prove that $S$ contains 3 distinct integers such that their product is a perfect cube.
|
Up to $(\dagger)$, we do the same as above and get 9 possible types:
$$
(a(\bmod 3), b(\bmod 3))=(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2)
$$
for $n=2^{a} 3^{b} \in S$.
Note that (i) among any 5 integers, there exist 3 whose sum is $0(\bmod 3)$, and that (ii) if $i, j, k \in\{0,1,2\}$, then $i+j+k \equiv 0(\bmod 3)$ if and only if $i=j=k$ or $\{i, j, k\}=\{0,1,2\}$.
Let's define
$T$ : the set of types of the integers in $S$;
$N(i)$ : the number of integers in $S$ of the type $(i, \cdot)$;
$M(i)$ : the number of integers $j \in\{0,1,2\}$ such that $(i, j) \in T$.
If $N(i) \geq 5$ for some $i$, the result follows from (i). Otherwise, for some permutation $(i, j, k)$ of $(0,1,2)$,
$$
N(i) \geq 3, \quad N(j) \geq 3, \quad N(k) \geq 1
$$
If $M(i)$ or $M(j)$ is 1 or 3 , the result follows from (ii). Otherwise $M(i)=M(j)=2$. Then either
$$
(i, x),(i, y),(j, x),(j, y) \in T \quad \text { or } \quad(i, x),(i, y),(j, x),(j, z) \in T
$$
for some permutation $(x, y, z)$ of $(0,1,2)$. Since $N(k) \geq 1$, at least one of $(k, x),(k, y)$ and $(k, z)$ contained in $T$. Therefore, in any case, the result follows from (ii). (For example, if $(k, y) \in T$, then take $(i, y),(j, y),(k, y)$ or $(i, x),(j, z),(k, y)$ from T.)
|
{
"resource_path": "APMO/segmented/en-apmo2007_sol.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSecond solution."
}
|
cb1a75c0-029c-534e-9491-d72a61bf40f2
| 605,094
|
Let $A B C$ be an acute angled triangle with $\angle B A C=60^{\circ}$ and $A B>A C$. Let $I$ be the incenter, and $H$ the orthocenter of the triangle $A B C$. Prove that
$$
2 \angle A H I=3 \angle A B C .
$$
|
Let $D$ be the intersection point of the lines $A H$ and $B C$. Let $K$ be the intersection point of the circumcircle $O$ of the triangle $A B C$ and the line $A H$. Let the line through $I$ perpendicular to $B C$ meet $B C$ and the minor arc $B C$ of the circumcircle $O$ at $E$ and $N$, respectively. We have
$\angle B I C=180^{\circ}-(\angle I B C+\angle I C B)=180^{\circ}-\frac{1}{2}(\angle A B C+\angle A C B)=90^{\circ}+\frac{1}{2} \angle B A C=120^{\circ}$
and also $\angle B N C=180^{\circ}-\angle B A C=120^{\circ}=\angle B I C$. Since $I N \perp B C$, the quadrilateral $B I C N$ is a kite and thus $I E=E N$.
Now, since $H$ is the orthocenter of the triangle $A B C, H D=D K$. Also because $E D \perp I N$ and $E D \perp H K$, we conclude that $I H K N$ is an isosceles trapezoid with $I H=N K$.
Hence
$$
\angle A H I=180^{\circ}-\angle I H K=180^{\circ}-\angle A K N=\angle A B N .
$$
Since $I E=E N$ and $B E \perp I N$, the triangles $I B E$ and $N B E$ are congruent. Therefore
$$
\angle N B E=\angle I B E=\angle I B C=\angle I B A=\frac{1}{2} \angle A B C
$$
and thus
$$
\angle A H I=\angle A B N=\frac{3}{2} \angle A B C .
$$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute angled triangle with $\angle B A C=60^{\circ}$ and $A B>A C$. Let $I$ be the incenter, and $H$ the orthocenter of the triangle $A B C$. Prove that
$$
2 \angle A H I=3 \angle A B C .
$$
|
Let $D$ be the intersection point of the lines $A H$ and $B C$. Let $K$ be the intersection point of the circumcircle $O$ of the triangle $A B C$ and the line $A H$. Let the line through $I$ perpendicular to $B C$ meet $B C$ and the minor arc $B C$ of the circumcircle $O$ at $E$ and $N$, respectively. We have
$\angle B I C=180^{\circ}-(\angle I B C+\angle I C B)=180^{\circ}-\frac{1}{2}(\angle A B C+\angle A C B)=90^{\circ}+\frac{1}{2} \angle B A C=120^{\circ}$
and also $\angle B N C=180^{\circ}-\angle B A C=120^{\circ}=\angle B I C$. Since $I N \perp B C$, the quadrilateral $B I C N$ is a kite and thus $I E=E N$.
Now, since $H$ is the orthocenter of the triangle $A B C, H D=D K$. Also because $E D \perp I N$ and $E D \perp H K$, we conclude that $I H K N$ is an isosceles trapezoid with $I H=N K$.
Hence
$$
\angle A H I=180^{\circ}-\angle I H K=180^{\circ}-\angle A K N=\angle A B N .
$$
Since $I E=E N$ and $B E \perp I N$, the triangles $I B E$ and $N B E$ are congruent. Therefore
$$
\angle N B E=\angle I B E=\angle I B C=\angle I B A=\frac{1}{2} \angle A B C
$$
and thus
$$
\angle A H I=\angle A B N=\frac{3}{2} \angle A B C .
$$
|
{
"resource_path": "APMO/segmented/en-apmo2007_sol.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution."
}
|
bf88f2c2-e0fd-5cc3-9f01-ea337ecb05fb
| 605,119
|
Let $A B C$ be an acute angled triangle with $\angle B A C=60^{\circ}$ and $A B>A C$. Let $I$ be the incenter, and $H$ the orthocenter of the triangle $A B C$. Prove that
$$
2 \angle A H I=3 \angle A B C .
$$
|
Let $P, Q$ and $R$ be the intersection points of $B H, C H$ and $A H$ with $A C, A B$ and $B C$, respectively. Then we have $\angle I B H=\angle I C H$. Indeed,
$$
\angle I B H=\angle A B P-\angle A B I=30^{\circ}-\frac{1}{2} \angle A B C
$$
and
$$
\angle I C H=\angle A C I-\angle A C H=\frac{1}{2} \angle A C B-30^{\circ}=30^{\circ}-\frac{1}{2} \angle A B C,
$$
because $\angle A B H=\angle A C H=30^{\circ}$ and $\angle A C B+\angle A B C=120^{\circ}$. (Note that $\angle A B P>\angle A B I$ and $\angle A C I>\angle A C H$ because $A B$ is the longest side of the triangle $A B C$ under the given conditions.) Therefore BIHC is a cyclic quadrilateral and thus
$$
\angle B H I=\angle B C I=\frac{1}{2} \angle A C B .
$$
On the other hand,
$$
\angle B H R=90^{\circ}-\angle H B R=90^{\circ}-(\angle A B C-\angle A B H)=120^{\circ}-\angle A B C
$$
Therefore,
$$
\begin{aligned}
\angle A H I & =180^{\circ}-\angle B H I-\angle B H R=60^{\circ}-\frac{1}{2} \angle A C B+\angle A B C \\
& =60^{\circ}-\frac{1}{2}\left(120^{\circ}-\angle A B C\right)+\angle A B C=\frac{3}{2} \angle A B C .
\end{aligned}
$$
|
2 \angle A H I=3 \angle A B C
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute angled triangle with $\angle B A C=60^{\circ}$ and $A B>A C$. Let $I$ be the incenter, and $H$ the orthocenter of the triangle $A B C$. Prove that
$$
2 \angle A H I=3 \angle A B C .
$$
|
Let $P, Q$ and $R$ be the intersection points of $B H, C H$ and $A H$ with $A C, A B$ and $B C$, respectively. Then we have $\angle I B H=\angle I C H$. Indeed,
$$
\angle I B H=\angle A B P-\angle A B I=30^{\circ}-\frac{1}{2} \angle A B C
$$
and
$$
\angle I C H=\angle A C I-\angle A C H=\frac{1}{2} \angle A C B-30^{\circ}=30^{\circ}-\frac{1}{2} \angle A B C,
$$
because $\angle A B H=\angle A C H=30^{\circ}$ and $\angle A C B+\angle A B C=120^{\circ}$. (Note that $\angle A B P>\angle A B I$ and $\angle A C I>\angle A C H$ because $A B$ is the longest side of the triangle $A B C$ under the given conditions.) Therefore BIHC is a cyclic quadrilateral and thus
$$
\angle B H I=\angle B C I=\frac{1}{2} \angle A C B .
$$
On the other hand,
$$
\angle B H R=90^{\circ}-\angle H B R=90^{\circ}-(\angle A B C-\angle A B H)=120^{\circ}-\angle A B C
$$
Therefore,
$$
\begin{aligned}
\angle A H I & =180^{\circ}-\angle B H I-\angle B H R=60^{\circ}-\frac{1}{2} \angle A C B+\angle A B C \\
& =60^{\circ}-\frac{1}{2}\left(120^{\circ}-\angle A B C\right)+\angle A B C=\frac{3}{2} \angle A B C .
\end{aligned}
$$
|
{
"resource_path": "APMO/segmented/en-apmo2007_sol.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSecond solution."
}
|
bf88f2c2-e0fd-5cc3-9f01-ea337ecb05fb
| 605,119
|
Consider $n$ disks $C_{1}, C_{2}, \ldots, C_{n}$ in a plane such that for each $1 \leq i<n$, the center of $C_{i}$ is on the circumference of $C_{i+1}$, and the center of $C_{n}$ is on the circumference of $C_{1}$. Define the score of such an arrangement of $n$ disks to be the number of pairs $(i, j)$ for which $C_{i}$ properly contains $C_{j}$. Determine the maximum possible score.
|
The answer is $(n-1)(n-2) / 2$.
Let's call a set of $n$ disks satisfying the given conditions an $n$-configuration. For an $n$ configuration $\mathcal{C}=\left\{C_{1}, \ldots, C_{n}\right\}$, let $S_{\mathcal{C}}=\left\{(i, j) \mid C_{i}\right.$ properly contains $\left.C_{j}\right\}$. So, the score of an $n$-configuration $\mathcal{C}$ is $\left|S_{\mathcal{C}}\right|$.
We'll show that (i) there is an $n$-configuration $\mathcal{C}$ for which $\left|S_{\mathcal{C}}\right|=(n-1)(n-2) / 2$, and that (ii) $\left|S_{\mathcal{C}}\right| \leq(n-1)(n-2) / 2$ for any $n$-configuration $\mathcal{C}$.
Let $C_{1}$ be any disk. Then for $i=2, \ldots, n-1$, take $C_{i}$ inside $C_{i-1}$ so that the circumference of $C_{i}$ contains the center of $C_{i-1}$. Finally, let $C_{n}$ be a disk whose center is on the circumference of $C_{1}$ and whose circumference contains the center of $C_{n-1}$. This gives $S_{\mathcal{C}}=\{(i, j) \mid 1 \leq i<j \leq n-1\}$ of size $(n-1)(n-2) / 2$, which proves (i).
For any $n$-configuration $\mathcal{C}, S_{\mathcal{C}}$ must satisfy the following properties:
(1) $(i, i) \notin S_{\mathcal{C}}$,
(2) $(i+1, i) \notin S_{\mathcal{C}},(1, n) \notin S_{\mathcal{C}}$,
(3) if $(i, j),(j, k) \in S_{\mathcal{C}}$, then $(i, k) \in S_{\mathcal{C}}$,
(4) if $(i, j) \in S_{\mathcal{C}}$, then $(j, i) \notin S_{\mathcal{C}}$.
Now we show that a set $G$ of ordered pairs of integers between 1 and $n$, satisfying the conditions $(1) \sim(4)$, can have no more than $(n-1)(n-2) / 2$ elements. Suppose that there exists a set $G$ that satisfies the conditions (1) $\sim(4)$, and has more than $(n-1)(n-2) / 2$ elements. Let $n$ be the least positive integer with which there exists such a set $G$. Note that $G$ must have $(i, i+1)$ for some $1 \leq i \leq n$ or $(n, 1)$, since otherwise $G$ can have at most
$$
\binom{n}{2}-n=\frac{n(n-3)}{2}<\frac{(n-1)(n-2)}{2}
$$
elements. Without loss of generality we may assume that $(n, 1) \in G$. Then $(1, n-1) \notin G$, since otherwise the condition (3) yields $(n, n-1) \in G$ contradicting the condition (2). Now let $G^{\prime}=\{(i, j) \in G \mid 1 \leq i, j \leq n-1\}$, then $G^{\prime}$ satisfies the conditions (1) (4), with $n-1$.
We now claim that $\left|G-G^{\prime}\right| \leq n-2$ :
Suppose that $\left|G-G^{\prime}\right|>n-2$, then $\left|G-G^{\prime}\right|=n-1$ and hence for each $1 \leq i \leq n-1$, either $(i, n)$ or $(n, i)$ must be in $G$. We already know that $(n, 1) \in G$ and $(n-1, n) \in G$ (because $(n, n-1) \notin G$ ) and this implies that $(n, n-2) \notin G$ and $(n-2, n) \in G$. If we keep doing this process, we obtain $(1, n) \in G$, which is a contradiction.
Since $\left|G-G^{\prime}\right| \leq n-2$, we obtain
$$
\left|G^{\prime}\right| \geq \frac{(n-1)(n-2)}{2}-(n-2)=\frac{(n-2)(n-3)}{2}
$$
This, however, contradicts the minimality of $n$, and hence proves (ii).
|
(n-1)(n-2) / 2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Consider $n$ disks $C_{1}, C_{2}, \ldots, C_{n}$ in a plane such that for each $1 \leq i<n$, the center of $C_{i}$ is on the circumference of $C_{i+1}$, and the center of $C_{n}$ is on the circumference of $C_{1}$. Define the score of such an arrangement of $n$ disks to be the number of pairs $(i, j)$ for which $C_{i}$ properly contains $C_{j}$. Determine the maximum possible score.
|
The answer is $(n-1)(n-2) / 2$.
Let's call a set of $n$ disks satisfying the given conditions an $n$-configuration. For an $n$ configuration $\mathcal{C}=\left\{C_{1}, \ldots, C_{n}\right\}$, let $S_{\mathcal{C}}=\left\{(i, j) \mid C_{i}\right.$ properly contains $\left.C_{j}\right\}$. So, the score of an $n$-configuration $\mathcal{C}$ is $\left|S_{\mathcal{C}}\right|$.
We'll show that (i) there is an $n$-configuration $\mathcal{C}$ for which $\left|S_{\mathcal{C}}\right|=(n-1)(n-2) / 2$, and that (ii) $\left|S_{\mathcal{C}}\right| \leq(n-1)(n-2) / 2$ for any $n$-configuration $\mathcal{C}$.
Let $C_{1}$ be any disk. Then for $i=2, \ldots, n-1$, take $C_{i}$ inside $C_{i-1}$ so that the circumference of $C_{i}$ contains the center of $C_{i-1}$. Finally, let $C_{n}$ be a disk whose center is on the circumference of $C_{1}$ and whose circumference contains the center of $C_{n-1}$. This gives $S_{\mathcal{C}}=\{(i, j) \mid 1 \leq i<j \leq n-1\}$ of size $(n-1)(n-2) / 2$, which proves (i).
For any $n$-configuration $\mathcal{C}, S_{\mathcal{C}}$ must satisfy the following properties:
(1) $(i, i) \notin S_{\mathcal{C}}$,
(2) $(i+1, i) \notin S_{\mathcal{C}},(1, n) \notin S_{\mathcal{C}}$,
(3) if $(i, j),(j, k) \in S_{\mathcal{C}}$, then $(i, k) \in S_{\mathcal{C}}$,
(4) if $(i, j) \in S_{\mathcal{C}}$, then $(j, i) \notin S_{\mathcal{C}}$.
Now we show that a set $G$ of ordered pairs of integers between 1 and $n$, satisfying the conditions $(1) \sim(4)$, can have no more than $(n-1)(n-2) / 2$ elements. Suppose that there exists a set $G$ that satisfies the conditions (1) $\sim(4)$, and has more than $(n-1)(n-2) / 2$ elements. Let $n$ be the least positive integer with which there exists such a set $G$. Note that $G$ must have $(i, i+1)$ for some $1 \leq i \leq n$ or $(n, 1)$, since otherwise $G$ can have at most
$$
\binom{n}{2}-n=\frac{n(n-3)}{2}<\frac{(n-1)(n-2)}{2}
$$
elements. Without loss of generality we may assume that $(n, 1) \in G$. Then $(1, n-1) \notin G$, since otherwise the condition (3) yields $(n, n-1) \in G$ contradicting the condition (2). Now let $G^{\prime}=\{(i, j) \in G \mid 1 \leq i, j \leq n-1\}$, then $G^{\prime}$ satisfies the conditions (1) (4), with $n-1$.
We now claim that $\left|G-G^{\prime}\right| \leq n-2$ :
Suppose that $\left|G-G^{\prime}\right|>n-2$, then $\left|G-G^{\prime}\right|=n-1$ and hence for each $1 \leq i \leq n-1$, either $(i, n)$ or $(n, i)$ must be in $G$. We already know that $(n, 1) \in G$ and $(n-1, n) \in G$ (because $(n, n-1) \notin G$ ) and this implies that $(n, n-2) \notin G$ and $(n-2, n) \in G$. If we keep doing this process, we obtain $(1, n) \in G$, which is a contradiction.
Since $\left|G-G^{\prime}\right| \leq n-2$, we obtain
$$
\left|G^{\prime}\right| \geq \frac{(n-1)(n-2)}{2}-(n-2)=\frac{(n-2)(n-3)}{2}
$$
This, however, contradicts the minimality of $n$, and hence proves (ii).
|
{
"resource_path": "APMO/segmented/en-apmo2007_sol.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "\nSolution."
}
|
8d33c1d3-c1d3-5bf1-b208-ed86249f3b44
| 261,138
|
Let $x, y$ and $z$ be positive real numbers such that $\sqrt{x}+\sqrt{y}+\sqrt{z}=1$. Prove that
$$
\frac{x^{2}+y z}{\sqrt{2 x^{2}(y+z)}}+\frac{y^{2}+z x}{\sqrt{2 y^{2}(z+x)}}+\frac{z^{2}+x y}{\sqrt{2 z^{2}(x+y)}} \geq 1
$$
|
We first note that
$$
\begin{aligned}
\frac{x^{2}+y z}{\sqrt{2 x^{2}(y+z)}} & =\frac{x^{2}-x(y+z)+y z}{\sqrt{2 x^{2}(y+z)}}+\frac{x(y+z)}{\sqrt{2 x^{2}(y+z)}} \\
& =\frac{(x-y)(x-z)}{\sqrt{2 x^{2}(y+z)}}+\sqrt{\frac{y+z}{2}} \\
& \geq \frac{(x-y)(x-z)}{\sqrt{2 x^{2}(y+z)}}+\frac{\sqrt{y}+\sqrt{z}}{2} .
\end{aligned}
$$
Similarly, we have
$$
\begin{aligned}
& \frac{y^{2}+z x}{\sqrt{2 y^{2}(z+x)}} \geq \frac{(y-z)(y-x)}{\sqrt{2 y^{2}(z+x)}}+\frac{\sqrt{z}+\sqrt{x}}{2}, \\
& \frac{z^{2}+x y}{\sqrt{2 z^{2}(x+y)}} \geq \frac{(z-x)(z-y)}{\sqrt{2 z^{2}(x+y)}}+\frac{\sqrt{x}+\sqrt{y}}{2} .
\end{aligned}
$$
We now add (1) (3) to get
$$
\begin{aligned}
& \frac{x^{2}+y z}{\sqrt{2 x^{2}(y+z)}}+\frac{y^{2}+z x}{\sqrt{2 y^{2}(z+x)}}+\frac{z^{2}+x y}{\sqrt{2 z^{2}(x+y)}} \\
& \geq \frac{(x-y)(x-z)}{\sqrt{2 x^{2}(y+z)}}+\frac{(y-z)(y-x)}{\sqrt{2 y^{2}(z+x)}}+\frac{(z-x)(z-y)}{\sqrt{2 z^{2}(x+y)}}+\sqrt{x}+\sqrt{y}+\sqrt{z} \\
& =\frac{(x-y)(x-z)}{\sqrt{2 x^{2}(y+z)}}+\frac{(y-z)(y-x)}{\sqrt{2 y^{2}(z+x)}}+\frac{(z-x)(z-y)}{\sqrt{2 z^{2}(x+y)}}+1 .
\end{aligned}
$$
Thus, it suffices to show that
$$
\frac{(x-y)(x-z)}{\sqrt{2 x^{2}(y+z)}}+\frac{(y-z)(y-x)}{\sqrt{2 y^{2}(z+x)}}+\frac{(z-x)(z-y)}{\sqrt{2 z^{2}(x+y)}} \geq 0 .
$$
Now, assume without loss of generality, that $x \geq y \geq z$. Then we have
$$
\frac{(x-y)(x-z)}{\sqrt{2 x^{2}(y+z)}} \geq 0
$$
and
$$
\begin{aligned}
& \frac{(z-x)(z-y)}{\sqrt{2 z^{2}(x+y)}}+\frac{(y-z)(y-x)}{\sqrt{2 y^{2}(z+x)}}=\frac{(y-z)(x-z)}{\sqrt{2 z^{2}(x+y)}}-\frac{(y-z)(x-y)}{\sqrt{2 y^{2}(z+x)}} \\
& \geq \frac{(y-z)(x-y)}{\sqrt{2 z^{2}(x+y)}}-\frac{(y-z)(x-y)}{\sqrt{2 y^{2}(z+x)}}=(y-z)(x-y)\left(\frac{1}{\sqrt{2 z^{2}(x+y)}}-\frac{1}{\sqrt{2 y^{2}(z+x)}}\right)
\end{aligned}
$$
The last quantity is non-negative due to the fact that
$$
y^{2}(z+x)=y^{2} z+y^{2} x \geq y z^{2}+z^{2} x=z^{2}(x+y)
$$
This completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $x, y$ and $z$ be positive real numbers such that $\sqrt{x}+\sqrt{y}+\sqrt{z}=1$. Prove that
$$
\frac{x^{2}+y z}{\sqrt{2 x^{2}(y+z)}}+\frac{y^{2}+z x}{\sqrt{2 y^{2}(z+x)}}+\frac{z^{2}+x y}{\sqrt{2 z^{2}(x+y)}} \geq 1
$$
|
We first note that
$$
\begin{aligned}
\frac{x^{2}+y z}{\sqrt{2 x^{2}(y+z)}} & =\frac{x^{2}-x(y+z)+y z}{\sqrt{2 x^{2}(y+z)}}+\frac{x(y+z)}{\sqrt{2 x^{2}(y+z)}} \\
& =\frac{(x-y)(x-z)}{\sqrt{2 x^{2}(y+z)}}+\sqrt{\frac{y+z}{2}} \\
& \geq \frac{(x-y)(x-z)}{\sqrt{2 x^{2}(y+z)}}+\frac{\sqrt{y}+\sqrt{z}}{2} .
\end{aligned}
$$
Similarly, we have
$$
\begin{aligned}
& \frac{y^{2}+z x}{\sqrt{2 y^{2}(z+x)}} \geq \frac{(y-z)(y-x)}{\sqrt{2 y^{2}(z+x)}}+\frac{\sqrt{z}+\sqrt{x}}{2}, \\
& \frac{z^{2}+x y}{\sqrt{2 z^{2}(x+y)}} \geq \frac{(z-x)(z-y)}{\sqrt{2 z^{2}(x+y)}}+\frac{\sqrt{x}+\sqrt{y}}{2} .
\end{aligned}
$$
We now add (1) (3) to get
$$
\begin{aligned}
& \frac{x^{2}+y z}{\sqrt{2 x^{2}(y+z)}}+\frac{y^{2}+z x}{\sqrt{2 y^{2}(z+x)}}+\frac{z^{2}+x y}{\sqrt{2 z^{2}(x+y)}} \\
& \geq \frac{(x-y)(x-z)}{\sqrt{2 x^{2}(y+z)}}+\frac{(y-z)(y-x)}{\sqrt{2 y^{2}(z+x)}}+\frac{(z-x)(z-y)}{\sqrt{2 z^{2}(x+y)}}+\sqrt{x}+\sqrt{y}+\sqrt{z} \\
& =\frac{(x-y)(x-z)}{\sqrt{2 x^{2}(y+z)}}+\frac{(y-z)(y-x)}{\sqrt{2 y^{2}(z+x)}}+\frac{(z-x)(z-y)}{\sqrt{2 z^{2}(x+y)}}+1 .
\end{aligned}
$$
Thus, it suffices to show that
$$
\frac{(x-y)(x-z)}{\sqrt{2 x^{2}(y+z)}}+\frac{(y-z)(y-x)}{\sqrt{2 y^{2}(z+x)}}+\frac{(z-x)(z-y)}{\sqrt{2 z^{2}(x+y)}} \geq 0 .
$$
Now, assume without loss of generality, that $x \geq y \geq z$. Then we have
$$
\frac{(x-y)(x-z)}{\sqrt{2 x^{2}(y+z)}} \geq 0
$$
and
$$
\begin{aligned}
& \frac{(z-x)(z-y)}{\sqrt{2 z^{2}(x+y)}}+\frac{(y-z)(y-x)}{\sqrt{2 y^{2}(z+x)}}=\frac{(y-z)(x-z)}{\sqrt{2 z^{2}(x+y)}}-\frac{(y-z)(x-y)}{\sqrt{2 y^{2}(z+x)}} \\
& \geq \frac{(y-z)(x-y)}{\sqrt{2 z^{2}(x+y)}}-\frac{(y-z)(x-y)}{\sqrt{2 y^{2}(z+x)}}=(y-z)(x-y)\left(\frac{1}{\sqrt{2 z^{2}(x+y)}}-\frac{1}{\sqrt{2 y^{2}(z+x)}}\right)
\end{aligned}
$$
The last quantity is non-negative due to the fact that
$$
y^{2}(z+x)=y^{2} z+y^{2} x \geq y z^{2}+z^{2} x=z^{2}(x+y)
$$
This completes the proof.
|
{
"resource_path": "APMO/segmented/en-apmo2007_sol.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "\nSolution."
}
|
2976be20-c465-5a41-b660-ed93dce21add
| 605,165
|
Let $x, y$ and $z$ be positive real numbers such that $\sqrt{x}+\sqrt{y}+\sqrt{z}=1$. Prove that
$$
\frac{x^{2}+y z}{\sqrt{2 x^{2}(y+z)}}+\frac{y^{2}+z x}{\sqrt{2 y^{2}(z+x)}}+\frac{z^{2}+x y}{\sqrt{2 z^{2}(x+y)}} \geq 1
$$
|
By Cauchy-Schwarz inequality,
$$
\begin{aligned}
& \left(\frac{x^{2}}{\sqrt{2 x^{2}(y+z)}}+\frac{y^{2}}{\sqrt{2 y^{2}(z+x)}}+\frac{z^{2}}{\sqrt{2 z^{2}(x+y)}}\right) \\
& \quad \times(\sqrt{2(y+z)}+\sqrt{2(z+x)}+\sqrt{2(x+y)}) \geq(\sqrt{x}+\sqrt{y}+\sqrt{z})^{2}=1
\end{aligned}
$$
and
$$
\begin{aligned}
& \left(\frac{y z}{\sqrt{2 x^{2}(y+z)}}+\frac{z x}{\sqrt{2 y^{2}(z+x)}}+\frac{x y}{\sqrt{2 z^{2}(x+y)}}\right) \\
& \quad \times(\sqrt{2(y+z)}+\sqrt{2(z+x)}+\sqrt{2(x+y)}) \geq\left(\sqrt{\frac{y z}{x}}+\sqrt{\frac{z x}{y}}+\sqrt{\frac{x y}{z}}\right)^{2}
\end{aligned}
$$
We now combine (5) and (6) to find
$$
\begin{aligned}
& \left(\frac{x^{2}+y z}{\sqrt{2 x^{2}(y+z)}}+\frac{y^{2}+z x}{\sqrt{2 y^{2}(z+x)}}+\frac{z^{2}+x y}{\sqrt{2 z^{2}(x+y)}}\right) \\
& \quad \times(\sqrt{2(x+y)}+\sqrt{2(y+z)}+\sqrt{2(z+x)}) \\
& \geq 1+\left(\sqrt{\frac{y z}{x}}+\sqrt{\frac{z x}{y}}+\sqrt{\frac{x y}{z}}\right)^{2} \geq 2\left(\sqrt{\frac{y z}{x}}+\sqrt{\frac{z x}{y}}+\sqrt{\frac{x y}{z}}\right) .
\end{aligned}
$$
Thus, it suffices to show that
$$
2\left(\sqrt{\frac{y z}{x}}+\sqrt{\frac{z x}{y}}+\sqrt{\frac{x y}{z}}\right) \geq \sqrt{2(y+z)}+\sqrt{2(z+x)}+\sqrt{2(x+y)}
$$
Consider the following inequality using AM-GM inequality
$$
\left[\sqrt{\frac{y z}{x}}+\left(\frac{1}{2} \sqrt{\frac{z x}{y}}+\frac{1}{2} \sqrt{\frac{x y}{z}}\right)\right]^{2} \geq 4 \sqrt{\frac{y z}{x}}\left(\frac{1}{2} \sqrt{\frac{z x}{y}}+\frac{1}{2} \sqrt{\frac{x y}{z}}\right)=2(y+z)
$$
or equivalently
$$
\sqrt{\frac{y z}{x}}+\left(\frac{1}{2} \sqrt{\frac{z x}{y}}+\frac{1}{2} \sqrt{\frac{x y}{z}}\right) \geq \sqrt{2(y+z)} .
$$
Similarly, we have
$$
\begin{aligned}
& \sqrt{\frac{z x}{y}}+\left(\frac{1}{2} \sqrt{\frac{x y}{z}}+\frac{1}{2} \sqrt{\frac{y z}{x}}\right) \geq \sqrt{2(z+x)} \\
& \sqrt{\frac{x y}{z}}+\left(\frac{1}{2} \sqrt{\frac{y z}{x}}+\frac{1}{2} \sqrt{\frac{z x}{y}}\right) \geq \sqrt{2(x+y)}
\end{aligned}
$$
Adding the last three inequalities, we get
$$
2\left(\sqrt{\frac{y z}{x}}+\sqrt{\frac{z x}{y}}+\sqrt{\frac{x y}{z}}\right) \geq \sqrt{2(y+z)}+\sqrt{2(z+x)}+\sqrt{2(x+y)} .
$$
This completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $x, y$ and $z$ be positive real numbers such that $\sqrt{x}+\sqrt{y}+\sqrt{z}=1$. Prove that
$$
\frac{x^{2}+y z}{\sqrt{2 x^{2}(y+z)}}+\frac{y^{2}+z x}{\sqrt{2 y^{2}(z+x)}}+\frac{z^{2}+x y}{\sqrt{2 z^{2}(x+y)}} \geq 1
$$
|
By Cauchy-Schwarz inequality,
$$
\begin{aligned}
& \left(\frac{x^{2}}{\sqrt{2 x^{2}(y+z)}}+\frac{y^{2}}{\sqrt{2 y^{2}(z+x)}}+\frac{z^{2}}{\sqrt{2 z^{2}(x+y)}}\right) \\
& \quad \times(\sqrt{2(y+z)}+\sqrt{2(z+x)}+\sqrt{2(x+y)}) \geq(\sqrt{x}+\sqrt{y}+\sqrt{z})^{2}=1
\end{aligned}
$$
and
$$
\begin{aligned}
& \left(\frac{y z}{\sqrt{2 x^{2}(y+z)}}+\frac{z x}{\sqrt{2 y^{2}(z+x)}}+\frac{x y}{\sqrt{2 z^{2}(x+y)}}\right) \\
& \quad \times(\sqrt{2(y+z)}+\sqrt{2(z+x)}+\sqrt{2(x+y)}) \geq\left(\sqrt{\frac{y z}{x}}+\sqrt{\frac{z x}{y}}+\sqrt{\frac{x y}{z}}\right)^{2}
\end{aligned}
$$
We now combine (5) and (6) to find
$$
\begin{aligned}
& \left(\frac{x^{2}+y z}{\sqrt{2 x^{2}(y+z)}}+\frac{y^{2}+z x}{\sqrt{2 y^{2}(z+x)}}+\frac{z^{2}+x y}{\sqrt{2 z^{2}(x+y)}}\right) \\
& \quad \times(\sqrt{2(x+y)}+\sqrt{2(y+z)}+\sqrt{2(z+x)}) \\
& \geq 1+\left(\sqrt{\frac{y z}{x}}+\sqrt{\frac{z x}{y}}+\sqrt{\frac{x y}{z}}\right)^{2} \geq 2\left(\sqrt{\frac{y z}{x}}+\sqrt{\frac{z x}{y}}+\sqrt{\frac{x y}{z}}\right) .
\end{aligned}
$$
Thus, it suffices to show that
$$
2\left(\sqrt{\frac{y z}{x}}+\sqrt{\frac{z x}{y}}+\sqrt{\frac{x y}{z}}\right) \geq \sqrt{2(y+z)}+\sqrt{2(z+x)}+\sqrt{2(x+y)}
$$
Consider the following inequality using AM-GM inequality
$$
\left[\sqrt{\frac{y z}{x}}+\left(\frac{1}{2} \sqrt{\frac{z x}{y}}+\frac{1}{2} \sqrt{\frac{x y}{z}}\right)\right]^{2} \geq 4 \sqrt{\frac{y z}{x}}\left(\frac{1}{2} \sqrt{\frac{z x}{y}}+\frac{1}{2} \sqrt{\frac{x y}{z}}\right)=2(y+z)
$$
or equivalently
$$
\sqrt{\frac{y z}{x}}+\left(\frac{1}{2} \sqrt{\frac{z x}{y}}+\frac{1}{2} \sqrt{\frac{x y}{z}}\right) \geq \sqrt{2(y+z)} .
$$
Similarly, we have
$$
\begin{aligned}
& \sqrt{\frac{z x}{y}}+\left(\frac{1}{2} \sqrt{\frac{x y}{z}}+\frac{1}{2} \sqrt{\frac{y z}{x}}\right) \geq \sqrt{2(z+x)} \\
& \sqrt{\frac{x y}{z}}+\left(\frac{1}{2} \sqrt{\frac{y z}{x}}+\frac{1}{2} \sqrt{\frac{z x}{y}}\right) \geq \sqrt{2(x+y)}
\end{aligned}
$$
Adding the last three inequalities, we get
$$
2\left(\sqrt{\frac{y z}{x}}+\sqrt{\frac{z x}{y}}+\sqrt{\frac{x y}{z}}\right) \geq \sqrt{2(y+z)}+\sqrt{2(z+x)}+\sqrt{2(x+y)} .
$$
This completes the proof.
|
{
"resource_path": "APMO/segmented/en-apmo2007_sol.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "\nSecond solution."
}
|
2976be20-c465-5a41-b660-ed93dce21add
| 605,165
|
A regular $(5 \times 5)$-array of lights is defective, so that toggling the switch for one light causes each adjacent light in the same row and in the same column as well as the light itself to change state, from on to off, or from off to on. Initially all the lights are switched off. After a certain number of toggles, exactly one light is switched on. Find all the possible positions of this light.
|
We assign the following first labels to the 25 positions of the lights:
| 1 | 1 | 0 | 1 | 1 |
| :--- | :--- | :--- | :--- | :--- |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 |
For each on-off combination of lights in the array, define its first value to be the sum of the first labels of those positions at which the lights are switched on. It is easy to check that toggling any switch always leads to an on-off combination of lights whose first value has the same parity(the remainder when divided by 2) as that of the previous on-off combination.
The $90^{\circ}$ rotation of the first labels gives us another labels (let us call it the second labels) which also makes the parity of the second value(the sum of the second labels of those positions at which the lights are switched on) invariant under toggling.
| 1 | 0 | 1 | 0 | 1 |
| :--- | :--- | :--- | :--- | :--- |
| 1 | 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
Since the parity of the first and the second values of the initial status is 0 , after certain number of toggles the parity must remain unchanged with respect to the first labels and the second labels as well. Therefore, if exactly one light is on after some number of toggles, the label of that position must be 0 with respect to both labels. Hence according to the above pictures, the possible positions are the ones marked with $*_{i}$ 's in the following picture:
| | | | | |
| :--- | :--- | :--- | :--- | :--- |
| | $*_{2}$ | | $*_{1}$ | |
| | | $*_{0}$ | | |
| | $*_{3}$ | | $*_{4}$ | |
| | | | | |
Now we demonstrate that all five positions are possible:
Toggling the positions checked by t (the order of toggling is irrelevant) in the first picture makes the center $\left(*_{0}\right)$ the only position with light on and the second picture makes the position $*_{1}$ the only position with light on. The other $*_{i}$ 's can be obtained by rotating the second picture appropriately.
| | t | | t | |
| :---: | :---: | :---: | :---: | :---: |
| t | t | | t | t |
| | t | | | |
| | | t | t | t |
| | | | t | |
|
not found
|
Yes
|
Yes
|
math-word-problem
|
Logic and Puzzles
|
A regular $(5 \times 5)$-array of lights is defective, so that toggling the switch for one light causes each adjacent light in the same row and in the same column as well as the light itself to change state, from on to off, or from off to on. Initially all the lights are switched off. After a certain number of toggles, exactly one light is switched on. Find all the possible positions of this light.
|
We assign the following first labels to the 25 positions of the lights:
| 1 | 1 | 0 | 1 | 1 |
| :--- | :--- | :--- | :--- | :--- |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 |
For each on-off combination of lights in the array, define its first value to be the sum of the first labels of those positions at which the lights are switched on. It is easy to check that toggling any switch always leads to an on-off combination of lights whose first value has the same parity(the remainder when divided by 2) as that of the previous on-off combination.
The $90^{\circ}$ rotation of the first labels gives us another labels (let us call it the second labels) which also makes the parity of the second value(the sum of the second labels of those positions at which the lights are switched on) invariant under toggling.
| 1 | 0 | 1 | 0 | 1 |
| :--- | :--- | :--- | :--- | :--- |
| 1 | 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
Since the parity of the first and the second values of the initial status is 0 , after certain number of toggles the parity must remain unchanged with respect to the first labels and the second labels as well. Therefore, if exactly one light is on after some number of toggles, the label of that position must be 0 with respect to both labels. Hence according to the above pictures, the possible positions are the ones marked with $*_{i}$ 's in the following picture:
| | | | | |
| :--- | :--- | :--- | :--- | :--- |
| | $*_{2}$ | | $*_{1}$ | |
| | | $*_{0}$ | | |
| | $*_{3}$ | | $*_{4}$ | |
| | | | | |
Now we demonstrate that all five positions are possible:
Toggling the positions checked by t (the order of toggling is irrelevant) in the first picture makes the center $\left(*_{0}\right)$ the only position with light on and the second picture makes the position $*_{1}$ the only position with light on. The other $*_{i}$ 's can be obtained by rotating the second picture appropriately.

| | t | | t | |
| :---: | :---: | :---: | :---: | :---: |
| t | t | | t | t |
| | t | | | |
| | | t | t | t |
| | | | t | |
|
{
"resource_path": "APMO/segmented/en-apmo2007_sol.jsonl",
"problem_match": "\nProblem 5.",
"solution_match": "\nSolution."
}
|
1c86fa7e-563a-55ed-80de-bc8c39b3dff2
| 261,152
|
Let $A B C$ be a triangle with $\angle A<60^{\circ}$. Let $X$ and $Y$ be the points on the sides $A B$ and $A C$, respectively, such that $C A+A X=C B+B X$ and $B A+A Y=B C+C Y$. Let $P$ be the point in the plane such that the lines $P X$ and $P Y$ are perpendicular to $A B$ and $A C$, respectively. Prove that $\angle B P C<120^{\circ}$.
|
Let $I$ be the incenter of $\triangle A B C$, and let the feet of the perpendiculars from $I$ to $A B$ and to $A C$ be $D$ and $E$, respectively. (Without loss of generality, we may assume that $A C$ is the longest side. Then $X$ lies on the line segment $A D$. Although $P$ may or may not lie inside $\triangle A B C$, the proof below works for both cases. Note that $P$ is on the line perpendicular to $A B$ passing through $X$.) Let $O$ be the midpoint of $I P$, and let the feet of the perpendiculars from $O$ to $A B$ and to $A C$ be $M$ and $N$, respectively. Then $M$ and $N$ are the midpoints of $D X$ and $E Y$, respectively.
The conditions on the points $X$ and $Y$ yield the equations
$$
A X=\frac{A B+B C-C A}{2} \quad \text { and } \quad A Y=\frac{B C+C A-A B}{2} .
$$
From $A D=A E=\frac{C A+A B-B C}{2}$, we obtain
$$
B D=A B-A D=A B-\frac{C A+A B-B C}{2}=\frac{A B+B C-C A}{2}=A X .
$$
Since $M$ is the midpoint of $D X$, it follows that $M$ is the midpoint of $A B$. Similarly, $N$ is the midpoint of $A C$. Therefore, the perpendicular bisectors of $A B$ and $A C$ meet at $O$, that is, $O$ is the circumcenter of $\triangle A B C$. Since $\angle B A C<60^{\circ}, O$ lies on the same side of $B C$ as the point $A$ and
$$
\angle B O C=2 \angle B A C
$$
We can compute $\angle B I C$ as follows:
$$
\begin{aligned}
\angle B I C & =180^{\circ}-\angle I B C-\angle I C B=180^{\circ}-\frac{1}{2} \angle A B C-\frac{1}{2} \angle A C B \\
& =180^{\circ}-\frac{1}{2}(\angle A B C+\angle A C B)=180^{\circ}-\frac{1}{2}\left(180^{\circ}-\angle B A C\right)=90^{\circ}+\frac{1}{2} \angle B A C
\end{aligned}
$$
It follows from $\angle B A C<60^{\circ}$ that
$$
2 \angle B A C<90^{\circ}+\frac{1}{2} \angle B A C, \quad \text { i.e., } \quad \angle B O C<\angle B I C \text {. }
$$
From this it follows that $I$ lies inside the circumcircle of the isosceles triangle $B O C$ because $O$ and $I$ lie on the same side of $B C$. However, as $O$ is the midpoint of $I P, P$ must lie outside the circumcircle of triangle $B O C$ and on the same side of $B C$ as $O$. Therefore
$$
\angle B P C<\angle B O C=2 \angle B A C<120^{\circ} .
$$
Remark. If one assumes that $\angle A$ is smaller than the other two, then it is clear that the line $P X$ (or the line perpendicular to $A B$ at $X$ if $P=X$ ) runs through the excenter $I_{C}$ of the excircle tangent to the side $A B$. Since $2 \angle A C I_{C}=\angle A C B$ and $B C<A C$, we have $2 \angle P C B>\angle C$. Similarly, $2 \angle P B C>\angle B$. Therefore,
$$
\angle B P C=180^{\circ}-(\angle P B C+\angle P C B)<180^{\circ}-\left(\frac{\angle B+\angle C}{2}\right)=90+\frac{\angle A}{2}<120^{\circ}
$$
In this way, a special case of the problem can be easily proved.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $\angle A<60^{\circ}$. Let $X$ and $Y$ be the points on the sides $A B$ and $A C$, respectively, such that $C A+A X=C B+B X$ and $B A+A Y=B C+C Y$. Let $P$ be the point in the plane such that the lines $P X$ and $P Y$ are perpendicular to $A B$ and $A C$, respectively. Prove that $\angle B P C<120^{\circ}$.
|
Let $I$ be the incenter of $\triangle A B C$, and let the feet of the perpendiculars from $I$ to $A B$ and to $A C$ be $D$ and $E$, respectively. (Without loss of generality, we may assume that $A C$ is the longest side. Then $X$ lies on the line segment $A D$. Although $P$ may or may not lie inside $\triangle A B C$, the proof below works for both cases. Note that $P$ is on the line perpendicular to $A B$ passing through $X$.) Let $O$ be the midpoint of $I P$, and let the feet of the perpendiculars from $O$ to $A B$ and to $A C$ be $M$ and $N$, respectively. Then $M$ and $N$ are the midpoints of $D X$ and $E Y$, respectively.

The conditions on the points $X$ and $Y$ yield the equations
$$
A X=\frac{A B+B C-C A}{2} \quad \text { and } \quad A Y=\frac{B C+C A-A B}{2} .
$$
From $A D=A E=\frac{C A+A B-B C}{2}$, we obtain
$$
B D=A B-A D=A B-\frac{C A+A B-B C}{2}=\frac{A B+B C-C A}{2}=A X .
$$
Since $M$ is the midpoint of $D X$, it follows that $M$ is the midpoint of $A B$. Similarly, $N$ is the midpoint of $A C$. Therefore, the perpendicular bisectors of $A B$ and $A C$ meet at $O$, that is, $O$ is the circumcenter of $\triangle A B C$. Since $\angle B A C<60^{\circ}, O$ lies on the same side of $B C$ as the point $A$ and
$$
\angle B O C=2 \angle B A C
$$
We can compute $\angle B I C$ as follows:
$$
\begin{aligned}
\angle B I C & =180^{\circ}-\angle I B C-\angle I C B=180^{\circ}-\frac{1}{2} \angle A B C-\frac{1}{2} \angle A C B \\
& =180^{\circ}-\frac{1}{2}(\angle A B C+\angle A C B)=180^{\circ}-\frac{1}{2}\left(180^{\circ}-\angle B A C\right)=90^{\circ}+\frac{1}{2} \angle B A C
\end{aligned}
$$
It follows from $\angle B A C<60^{\circ}$ that
$$
2 \angle B A C<90^{\circ}+\frac{1}{2} \angle B A C, \quad \text { i.e., } \quad \angle B O C<\angle B I C \text {. }
$$
From this it follows that $I$ lies inside the circumcircle of the isosceles triangle $B O C$ because $O$ and $I$ lie on the same side of $B C$. However, as $O$ is the midpoint of $I P, P$ must lie outside the circumcircle of triangle $B O C$ and on the same side of $B C$ as $O$. Therefore
$$
\angle B P C<\angle B O C=2 \angle B A C<120^{\circ} .
$$
Remark. If one assumes that $\angle A$ is smaller than the other two, then it is clear that the line $P X$ (or the line perpendicular to $A B$ at $X$ if $P=X$ ) runs through the excenter $I_{C}$ of the excircle tangent to the side $A B$. Since $2 \angle A C I_{C}=\angle A C B$ and $B C<A C$, we have $2 \angle P C B>\angle C$. Similarly, $2 \angle P B C>\angle B$. Therefore,
$$
\angle B P C=180^{\circ}-(\angle P B C+\angle P C B)<180^{\circ}-\left(\frac{\angle B+\angle C}{2}\right)=90+\frac{\angle A}{2}<120^{\circ}
$$
In this way, a special case of the problem can be easily proved.
|
{
"resource_path": "APMO/segmented/en-apmo2008_sol.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "(Solution)"
}
|
416c31d1-d8c4-560f-9c8e-280509bf2b72
| 605,211
|
Students in a class form groups each of which contains exactly three members such that any two distinct groups have at most one member in common. Prove that, when the class size is 46 , there is a set of 10 students in which no group is properly contained.
|
We let $C$ be the set of all 46 students in the class and let
$$
s:=\max \{|S|: S \subseteq C \text { such that } S \text { contains no group properly }\}
$$
Then it suffices to prove that $s \geq 10$. (If $|S|=s>10$, we may choose a subset of $S$ consisting of 10 students.)
Suppose that $s \leq 9$ and let $S$ be a set of size $s$ in which no group is properly contained. Take any student, say $v$, from outside $S$. Because of the maximality of $s$, there should be a group containing the student $v$ and two other students in $S$. The number of ways to choose two students from $S$ is
$$
\binom{s}{2} \leq\binom{ 9}{2}=36
$$
On the other hand, there are at least $37=46-9$ students outside of $S$. Thus, among those 37 students outside, there is at least one student, say $u$, who does not belong to any group containing two students in $S$ and one outside. This is because no two distinct groups have two members in common. But then, $S$ can be enlarged by including $u$, which is a contradiction.
Remark. One may choose a subset $S$ of $C$ that contains no group properly. Then, assuming $|S|<10$, prove that there is a student outside $S$, say $u$, who does not belong to any group containing two students in $S$. After enlarging $S$ by including $u$, prove that the enlarged $S$ still contains no group properly.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Students in a class form groups each of which contains exactly three members such that any two distinct groups have at most one member in common. Prove that, when the class size is 46 , there is a set of 10 students in which no group is properly contained.
|
We let $C$ be the set of all 46 students in the class and let
$$
s:=\max \{|S|: S \subseteq C \text { such that } S \text { contains no group properly }\}
$$
Then it suffices to prove that $s \geq 10$. (If $|S|=s>10$, we may choose a subset of $S$ consisting of 10 students.)
Suppose that $s \leq 9$ and let $S$ be a set of size $s$ in which no group is properly contained. Take any student, say $v$, from outside $S$. Because of the maximality of $s$, there should be a group containing the student $v$ and two other students in $S$. The number of ways to choose two students from $S$ is
$$
\binom{s}{2} \leq\binom{ 9}{2}=36
$$
On the other hand, there are at least $37=46-9$ students outside of $S$. Thus, among those 37 students outside, there is at least one student, say $u$, who does not belong to any group containing two students in $S$ and one outside. This is because no two distinct groups have two members in common. But then, $S$ can be enlarged by including $u$, which is a contradiction.
Remark. One may choose a subset $S$ of $C$ that contains no group properly. Then, assuming $|S|<10$, prove that there is a student outside $S$, say $u$, who does not belong to any group containing two students in $S$. After enlarging $S$ by including $u$, prove that the enlarged $S$ still contains no group properly.
|
{
"resource_path": "APMO/segmented/en-apmo2008_sol.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "(Solution)"
}
|
fc1b8cc1-65cf-5aa3-a777-4dd71b58a19f
| 605,225
|
Let $\Gamma$ be the circumcircle of a triangle $A B C$. A circle passing through points $A$ and $C$ meets the sides $B C$ and $B A$ at $D$ and $E$, respectively. The lines $A D$ and $C E$ meet $\Gamma$ again at $G$ and $H$, respectively. The tangent lines of $\Gamma$ at $A$ and $C$ meet the line $D E$ at $L$ and $M$, respectively. Prove that the lines $L H$ and $M G$ meet at $\Gamma$.
|
Let $M G$ meet $\Gamma$ at $P$. Since $\angle M C D=\angle C A E$ and $\angle M D C=\angle C A E$, we have $M C=M D$. Thus
$$
M D^{2}=M C^{2}=M G \cdot M P
$$
and hence $M D$ is tangent to the circumcircle of $\triangle D G P$. Therefore $\angle D G P=\angle E D P$.
Let $\Gamma^{\prime}$ be the circumcircle of $\triangle B D E$. If $B=P$, then, since $\angle B G D=\angle B D E$, the tangent lines of $\Gamma^{\prime}$ and $\Gamma$ at $B$ should coincide, that is $\Gamma^{\prime}$ is tangent to $\Gamma$ from inside. Let $B \neq P$. If $P$ lies in the same side of the line $B C$ as $G$, then we have
$$
\angle E D P+\angle A B P=180^{\circ}
$$
because $\angle D G P+\angle A B P=180^{\circ}$. That is, the quadrilateral $B P D E$ is cyclic, and hence $P$ is on the intersection of $\Gamma^{\prime}$ with $\Gamma$.
Otherwise,
$$
\angle E D P=\angle D G P=\angle A G P=\angle A B P=\angle E B P .
$$
Therefore the quadrilateral $P B D E$ is cyclic, and hence $P$ again is on the intersection of $\Gamma^{\prime}$ with $\Gamma$.
Similarly, if $L H$ meets $\Gamma$ at $Q$, we either have $Q=B$, in which case $\Gamma^{\prime}$ is tangent to $\Gamma$ from inside, or $Q \neq B$. In the latter case, $Q$ is on the intersection of $\Gamma^{\prime}$ with $\Gamma$. In either case, we have $P=Q$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\Gamma$ be the circumcircle of a triangle $A B C$. A circle passing through points $A$ and $C$ meets the sides $B C$ and $B A$ at $D$ and $E$, respectively. The lines $A D$ and $C E$ meet $\Gamma$ again at $G$ and $H$, respectively. The tangent lines of $\Gamma$ at $A$ and $C$ meet the line $D E$ at $L$ and $M$, respectively. Prove that the lines $L H$ and $M G$ meet at $\Gamma$.
|
Let $M G$ meet $\Gamma$ at $P$. Since $\angle M C D=\angle C A E$ and $\angle M D C=\angle C A E$, we have $M C=M D$. Thus
$$
M D^{2}=M C^{2}=M G \cdot M P
$$
and hence $M D$ is tangent to the circumcircle of $\triangle D G P$. Therefore $\angle D G P=\angle E D P$.
Let $\Gamma^{\prime}$ be the circumcircle of $\triangle B D E$. If $B=P$, then, since $\angle B G D=\angle B D E$, the tangent lines of $\Gamma^{\prime}$ and $\Gamma$ at $B$ should coincide, that is $\Gamma^{\prime}$ is tangent to $\Gamma$ from inside. Let $B \neq P$. If $P$ lies in the same side of the line $B C$ as $G$, then we have
$$
\angle E D P+\angle A B P=180^{\circ}
$$
because $\angle D G P+\angle A B P=180^{\circ}$. That is, the quadrilateral $B P D E$ is cyclic, and hence $P$ is on the intersection of $\Gamma^{\prime}$ with $\Gamma$.

Otherwise,
$$
\angle E D P=\angle D G P=\angle A G P=\angle A B P=\angle E B P .
$$
Therefore the quadrilateral $P B D E$ is cyclic, and hence $P$ again is on the intersection of $\Gamma^{\prime}$ with $\Gamma$.
Similarly, if $L H$ meets $\Gamma$ at $Q$, we either have $Q=B$, in which case $\Gamma^{\prime}$ is tangent to $\Gamma$ from inside, or $Q \neq B$. In the latter case, $Q$ is on the intersection of $\Gamma^{\prime}$ with $\Gamma$. In either case, we have $P=Q$.
|
{
"resource_path": "APMO/segmented/en-apmo2008_sol.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "(Solution)"
}
|
c0f9b626-0f74-5cf8-8e79-7f33add8bbf1
| 260,671
|
Consider the function $f: \mathbb{N}_{0} \rightarrow \mathbb{N}_{0}$, where $\mathbb{N}_{0}$ is the set of all non-negative integers, defined by the following conditions:
(i) $f(0)=0$,
(ii) $f(2 n)=2 f(n)$ and
(iii) $f(2 n+1)=n+2 f(n)$ for all $n \geq 0$.
(a) Determine the three sets $L:=\{n \mid f(n)<f(n+1)\}, E:=\{n \mid f(n)=f(n+1)\}$, and $G:=\{n \mid f(n)>f(n+1)\}$.
(b) For each $k \geq 0$, find a formula for $a_{k}:=\max \left\{f(n): 0 \leq n \leq 2^{k}\right\}$ in terms of $k$.
|
(a) Let
$$
L_{1}:=\{2 k: k>0\}, \quad E_{1}:=\{0\} \cup\{4 k+1: k \geq 0\}, \quad \text { and } G_{1}:=\{4 k+3: k \geq 0\} .
$$
We will show that $L_{1}=L, E_{1}=E$, and $G_{1}=G$. It suffices to verify that $L_{1} \subseteq E, E_{1} \subseteq E$, and $G_{1} \subseteq G$ because $L_{1}, E_{1}$, and $G_{1}$ are mutually disjoint and $L_{1} \cup E_{1} \cup G_{1}=\mathbb{N}_{0}$.
Firstly, if $k>0$, then $f(2 k)-f(2 k+1)=-k<0$ and therefore $L_{1} \subseteq L$.
Secondly, $f(0)=0$ and
$$
\begin{aligned}
& f(4 k+1)=2 k+2 f(2 k)=2 k+4 f(k) \\
& f(4 k+2)=2 f(2 k+1)=2(k+2 f(k))=2 k+4 f(k)
\end{aligned}
$$
for all $k \geq 0$. Thus, $E_{1} \subseteq E$.
Lastly, in order to prove $G_{1} \subset G$, we claim that $f(n+1)-f(n) \leq n$ for all $n$. (In fact, one can prove a stronger inequality : $f(n+1)-f(n) \leq n / 2$.) This is clearly true for even $n$ from the definition since for $n=2 t$,
$$
f(2 t+1)-f(2 t)=t \leq n
$$
If $n=2 t+1$ is odd, then (assuming inductively that the result holds for all nonnegative $m<n$ ), we have
$$
\begin{aligned}
f(n+1)-f(n) & =f(2 t+2)-f(2 t+1)=2 f(t+1)-t-2 f(t) \\
& =2(f(t+1)-f(t))-t \leq 2 t-t=t<n .
\end{aligned}
$$
For all $k \geq 0$,
$$
\begin{aligned}
& f(4 k+4)-f(4 k+3)=f(2(2 k+2))-f(2(2 k+1)+1) \\
& =4 f(k+1)-(2 k+1+2 f(2 k+1))=4 f(k+1)-(2 k+1+2 k+4 f(k)) \\
& =4(f(k+1)-f(k))-(4 k+1) \leq 4 k-(4 k+1)<0 .
\end{aligned}
$$
This proves $G_{1} \subseteq G$.
(b) Note that $a_{0}=a_{1}=f(1)=0$. Let $k \geq 2$ and let $N_{k}=\left\{0,1,2, \ldots, 2^{k}\right\}$. First we claim that the maximum $a_{k}$ occurs at the largest number in $G \cap N_{k}$, that is, $a_{k}=f\left(2^{k}-1\right)$. We use mathematical induction on $k$ to prove the claim. Note that $a_{2}=f(3)=f\left(2^{2}-1\right)$.
Now let $k \geq 3$. For every even number $2 t$ with $2^{k-1}+1<2 t \leq 2^{k}$,
$$
f(2 t)=2 f(t) \leq 2 a_{k-1}=2 f\left(2^{k-1}-1\right)
$$
by induction hypothesis. For every odd number $2 t+1$ with $2^{k-1}+1 \leq 2 t+1<2^{k}$,
$$
\begin{aligned}
f(2 t+1) & =t+2 f(t) \leq 2^{k-1}-1+2 f(t) \\
& \leq 2^{k-1}-1+2 a_{k-1}=2^{k-1}-1+2 f\left(2^{k-1}-1\right)
\end{aligned}
$$
again by induction hypothesis. Combining ( $\dagger$ ), ( $\ddagger$ ) and
$$
f\left(2^{k}-1\right)=f\left(2\left(2^{k-1}-1\right)+1\right)=2^{k-1}-1+2 f\left(2^{k-1}-1\right)
$$
we may conclude that $a_{k}=f\left(2^{k}-1\right)$ as desired.
Furthermore, we obtain
$$
a_{k}=2 a_{k-1}+2^{k-1}-1
$$
for all $k \geq 3$. Note that this recursive formula for $a_{k}$ also holds for $k \geq 0,1$ and 2 . Unwinding this recursive formula, we finally get
$$
\begin{aligned}
a_{k} & =2 a_{k-1}+2^{k-1}-1=2\left(2 a_{k-2}+2^{k-2}-1\right)+2^{k-1}-1 \\
& =2^{2} a_{k-2}+2 \cdot 2^{k-1}-2-1=2^{2}\left(2 a_{k-3}+2^{k-3}-1\right)+2 \cdot 2^{k-1}-2-1 \\
& =2^{3} a_{k-3}+3 \cdot 2^{k-1}-2^{2}-2-1 \\
& \vdots \\
& =2^{k} a_{0}+k 2^{k-1}-2^{k-1}-2^{k-2}-\ldots-2-1 \\
& =k 2^{k-1}-2^{k}+1 \quad \text { for all } k \geq 0 .
\end{aligned}
$$
|
a_{k} = k 2^{k-1} - 2^{k} + 1
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Consider the function $f: \mathbb{N}_{0} \rightarrow \mathbb{N}_{0}$, where $\mathbb{N}_{0}$ is the set of all non-negative integers, defined by the following conditions:
(i) $f(0)=0$,
(ii) $f(2 n)=2 f(n)$ and
(iii) $f(2 n+1)=n+2 f(n)$ for all $n \geq 0$.
(a) Determine the three sets $L:=\{n \mid f(n)<f(n+1)\}, E:=\{n \mid f(n)=f(n+1)\}$, and $G:=\{n \mid f(n)>f(n+1)\}$.
(b) For each $k \geq 0$, find a formula for $a_{k}:=\max \left\{f(n): 0 \leq n \leq 2^{k}\right\}$ in terms of $k$.
|
(a) Let
$$
L_{1}:=\{2 k: k>0\}, \quad E_{1}:=\{0\} \cup\{4 k+1: k \geq 0\}, \quad \text { and } G_{1}:=\{4 k+3: k \geq 0\} .
$$
We will show that $L_{1}=L, E_{1}=E$, and $G_{1}=G$. It suffices to verify that $L_{1} \subseteq E, E_{1} \subseteq E$, and $G_{1} \subseteq G$ because $L_{1}, E_{1}$, and $G_{1}$ are mutually disjoint and $L_{1} \cup E_{1} \cup G_{1}=\mathbb{N}_{0}$.
Firstly, if $k>0$, then $f(2 k)-f(2 k+1)=-k<0$ and therefore $L_{1} \subseteq L$.
Secondly, $f(0)=0$ and
$$
\begin{aligned}
& f(4 k+1)=2 k+2 f(2 k)=2 k+4 f(k) \\
& f(4 k+2)=2 f(2 k+1)=2(k+2 f(k))=2 k+4 f(k)
\end{aligned}
$$
for all $k \geq 0$. Thus, $E_{1} \subseteq E$.
Lastly, in order to prove $G_{1} \subset G$, we claim that $f(n+1)-f(n) \leq n$ for all $n$. (In fact, one can prove a stronger inequality : $f(n+1)-f(n) \leq n / 2$.) This is clearly true for even $n$ from the definition since for $n=2 t$,
$$
f(2 t+1)-f(2 t)=t \leq n
$$
If $n=2 t+1$ is odd, then (assuming inductively that the result holds for all nonnegative $m<n$ ), we have
$$
\begin{aligned}
f(n+1)-f(n) & =f(2 t+2)-f(2 t+1)=2 f(t+1)-t-2 f(t) \\
& =2(f(t+1)-f(t))-t \leq 2 t-t=t<n .
\end{aligned}
$$
For all $k \geq 0$,
$$
\begin{aligned}
& f(4 k+4)-f(4 k+3)=f(2(2 k+2))-f(2(2 k+1)+1) \\
& =4 f(k+1)-(2 k+1+2 f(2 k+1))=4 f(k+1)-(2 k+1+2 k+4 f(k)) \\
& =4(f(k+1)-f(k))-(4 k+1) \leq 4 k-(4 k+1)<0 .
\end{aligned}
$$
This proves $G_{1} \subseteq G$.
(b) Note that $a_{0}=a_{1}=f(1)=0$. Let $k \geq 2$ and let $N_{k}=\left\{0,1,2, \ldots, 2^{k}\right\}$. First we claim that the maximum $a_{k}$ occurs at the largest number in $G \cap N_{k}$, that is, $a_{k}=f\left(2^{k}-1\right)$. We use mathematical induction on $k$ to prove the claim. Note that $a_{2}=f(3)=f\left(2^{2}-1\right)$.
Now let $k \geq 3$. For every even number $2 t$ with $2^{k-1}+1<2 t \leq 2^{k}$,
$$
f(2 t)=2 f(t) \leq 2 a_{k-1}=2 f\left(2^{k-1}-1\right)
$$
by induction hypothesis. For every odd number $2 t+1$ with $2^{k-1}+1 \leq 2 t+1<2^{k}$,
$$
\begin{aligned}
f(2 t+1) & =t+2 f(t) \leq 2^{k-1}-1+2 f(t) \\
& \leq 2^{k-1}-1+2 a_{k-1}=2^{k-1}-1+2 f\left(2^{k-1}-1\right)
\end{aligned}
$$
again by induction hypothesis. Combining ( $\dagger$ ), ( $\ddagger$ ) and
$$
f\left(2^{k}-1\right)=f\left(2\left(2^{k-1}-1\right)+1\right)=2^{k-1}-1+2 f\left(2^{k-1}-1\right)
$$
we may conclude that $a_{k}=f\left(2^{k}-1\right)$ as desired.
Furthermore, we obtain
$$
a_{k}=2 a_{k-1}+2^{k-1}-1
$$
for all $k \geq 3$. Note that this recursive formula for $a_{k}$ also holds for $k \geq 0,1$ and 2 . Unwinding this recursive formula, we finally get
$$
\begin{aligned}
a_{k} & =2 a_{k-1}+2^{k-1}-1=2\left(2 a_{k-2}+2^{k-2}-1\right)+2^{k-1}-1 \\
& =2^{2} a_{k-2}+2 \cdot 2^{k-1}-2-1=2^{2}\left(2 a_{k-3}+2^{k-3}-1\right)+2 \cdot 2^{k-1}-2-1 \\
& =2^{3} a_{k-3}+3 \cdot 2^{k-1}-2^{2}-2-1 \\
& \vdots \\
& =2^{k} a_{0}+k 2^{k-1}-2^{k-1}-2^{k-2}-\ldots-2-1 \\
& =k 2^{k-1}-2^{k}+1 \quad \text { for all } k \geq 0 .
\end{aligned}
$$
|
{
"resource_path": "APMO/segmented/en-apmo2008_sol.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "(Solution)"
}
|
ddf4343f-7cff-5d8d-bf81-43139177d948
| 605,259
|
Let $a, b, c$ be integers satisfying $0<a<c-1$ and $1<b<c$. For each $k$, $0 \leq k \leq a$, let $r_{k}, 0 \leq r_{k}<c$, be the remainder of $k b$ when divided by $c$. Prove that the two sets $\left\{r_{0}, r_{1}, r_{2}, \ldots, r_{a}\right\}$ and $\{0,1,2, \ldots, a\}$ are different.
|
Suppose that two sets are equal. Then $\operatorname{gcd}(b, c)=1$ and the polynomial
$$
f(x):=\left(1+x^{b}+x^{2 b}+\cdots+x^{a b}\right)-\left(1+x+x^{2}+\cdots+x^{a-1}+x^{a}\right)
$$
is divisible by $x^{c}-1$. (This is because: $m=n+c q \Longrightarrow x^{m}-x^{n}=x^{n+c q}-x^{n}=x^{n}\left(x^{c q}-1\right)$ and $\left(x^{c q}-1\right)=\left(x^{c}-1\right)\left(\left(x^{c}\right)^{q-1}+\left(x^{c}\right)^{q-2}+\cdots+1\right)$.) From
$$
f(x)=\frac{x^{(a+1) b}-1}{x^{b}-1}-\frac{x^{a+1}-1}{x-1}=\frac{F(x)}{(x-1)\left(x^{b}-1\right)}
$$
where $F(x)=x^{a b+b+1}+x^{b}+x^{a+1}-x^{a b+b}-x^{a+b+1}-x$, we have
$$
F(x) \equiv 0 \quad\left(\bmod x^{c}-1\right)
$$
Since $x^{c} \equiv 1\left(\bmod x^{c}-1\right)$, we may conclude that
$$
\{a b+b+1, b, a+1\} \equiv\{a b+b, a+b+1,1\} \quad(\bmod c)
$$
Thus,
$$
b \equiv a b+b, a+b+1 \text { or } 1(\bmod c)
$$
But neither $b \equiv 1(\bmod c)$ nor $b \equiv a+b+1(\bmod c)$ are possible by the given conditions. Therefore, $b \equiv a b+b(\bmod c)$. But this is also impossible because $\operatorname{gcd}(b, c)=1$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a, b, c$ be integers satisfying $0<a<c-1$ and $1<b<c$. For each $k$, $0 \leq k \leq a$, let $r_{k}, 0 \leq r_{k}<c$, be the remainder of $k b$ when divided by $c$. Prove that the two sets $\left\{r_{0}, r_{1}, r_{2}, \ldots, r_{a}\right\}$ and $\{0,1,2, \ldots, a\}$ are different.
|
Suppose that two sets are equal. Then $\operatorname{gcd}(b, c)=1$ and the polynomial
$$
f(x):=\left(1+x^{b}+x^{2 b}+\cdots+x^{a b}\right)-\left(1+x+x^{2}+\cdots+x^{a-1}+x^{a}\right)
$$
is divisible by $x^{c}-1$. (This is because: $m=n+c q \Longrightarrow x^{m}-x^{n}=x^{n+c q}-x^{n}=x^{n}\left(x^{c q}-1\right)$ and $\left(x^{c q}-1\right)=\left(x^{c}-1\right)\left(\left(x^{c}\right)^{q-1}+\left(x^{c}\right)^{q-2}+\cdots+1\right)$.) From
$$
f(x)=\frac{x^{(a+1) b}-1}{x^{b}-1}-\frac{x^{a+1}-1}{x-1}=\frac{F(x)}{(x-1)\left(x^{b}-1\right)}
$$
where $F(x)=x^{a b+b+1}+x^{b}+x^{a+1}-x^{a b+b}-x^{a+b+1}-x$, we have
$$
F(x) \equiv 0 \quad\left(\bmod x^{c}-1\right)
$$
Since $x^{c} \equiv 1\left(\bmod x^{c}-1\right)$, we may conclude that
$$
\{a b+b+1, b, a+1\} \equiv\{a b+b, a+b+1,1\} \quad(\bmod c)
$$
Thus,
$$
b \equiv a b+b, a+b+1 \text { or } 1(\bmod c)
$$
But neither $b \equiv 1(\bmod c)$ nor $b \equiv a+b+1(\bmod c)$ are possible by the given conditions. Therefore, $b \equiv a b+b(\bmod c)$. But this is also impossible because $\operatorname{gcd}(b, c)=1$.
|
{
"resource_path": "APMO/segmented/en-apmo2008_sol.jsonl",
"problem_match": "\nProblem 5.",
"solution_match": "(Solution)"
}
|
3830ebdd-4bb9-511f-b0cd-2a146406404f
| 260,687
|
Consider the following operation on positive real numbers written on a blackboard:
Choose a number $r$ written on the blackboard, erase that number, and then write a pair of positive real numbers $a$ and $b$ satisfying the condition $2 r^{2}=a b$ on the board.
Assume that you start out with just one positive real number $r$ on the blackboard, and apply this operation $k^{2}-1$ times to end up with $k^{2}$ positive real numbers, not necessarily distinct. Show that there exists a number on the board which does not exceed $k r$.
|
Using AM-GM inequality, we obtain
$$
\frac{1}{r^{2}}=\frac{2}{a b}=\frac{2 a b}{a^{2} b^{2}} \leq \frac{a^{2}+b^{2}}{a^{2} b^{2}} \leq \frac{1}{a^{2}}+\frac{1}{b^{2}}
$$
Consequently, if we let $S_{\ell}$ be the sum of the squares of the reciprocals of the numbers written on the board after $\ell$ operations, then $S_{\ell}$ increases as $\ell$ increases, that is,
$$
S_{0} \leq S_{1} \leq \cdots \leq S_{k^{2}-1}
$$
Therefore if we let $s$ be the smallest real number written on the board after $k^{2}-1$ operations, then $\frac{1}{s^{2}} \geq \frac{1}{t^{2}}$ for any number $t$ among $k^{2}$ numbers on the board and hence
$$
k^{2} \times \frac{1}{s^{2}} \geq S_{k^{2}-1} \geq S_{0}=\frac{1}{r^{2}}
$$
which implies that $s \leq k r$ as desired.
Remark. The nature of the problem does not change at all if the numbers on the board are restricted to be positive integers. But that may mislead some contestants to think the problem is a number theoretic problem rather than a combinatorial problem.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Consider the following operation on positive real numbers written on a blackboard:
Choose a number $r$ written on the blackboard, erase that number, and then write a pair of positive real numbers $a$ and $b$ satisfying the condition $2 r^{2}=a b$ on the board.
Assume that you start out with just one positive real number $r$ on the blackboard, and apply this operation $k^{2}-1$ times to end up with $k^{2}$ positive real numbers, not necessarily distinct. Show that there exists a number on the board which does not exceed $k r$.
|
Using AM-GM inequality, we obtain
$$
\frac{1}{r^{2}}=\frac{2}{a b}=\frac{2 a b}{a^{2} b^{2}} \leq \frac{a^{2}+b^{2}}{a^{2} b^{2}} \leq \frac{1}{a^{2}}+\frac{1}{b^{2}}
$$
Consequently, if we let $S_{\ell}$ be the sum of the squares of the reciprocals of the numbers written on the board after $\ell$ operations, then $S_{\ell}$ increases as $\ell$ increases, that is,
$$
S_{0} \leq S_{1} \leq \cdots \leq S_{k^{2}-1}
$$
Therefore if we let $s$ be the smallest real number written on the board after $k^{2}-1$ operations, then $\frac{1}{s^{2}} \geq \frac{1}{t^{2}}$ for any number $t$ among $k^{2}$ numbers on the board and hence
$$
k^{2} \times \frac{1}{s^{2}} \geq S_{k^{2}-1} \geq S_{0}=\frac{1}{r^{2}}
$$
which implies that $s \leq k r$ as desired.
Remark. The nature of the problem does not change at all if the numbers on the board are restricted to be positive integers. But that may mislead some contestants to think the problem is a number theoretic problem rather than a combinatorial problem.
|
{
"resource_path": "APMO/segmented/en-apmo2009_sol.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "(Solution)"
}
|
c4b367ea-94e5-56c6-9195-665d13c451fa
| 260,905
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.